银符考试题库B12
现在是:
试卷总分:100.0
您的得分:
考试时间为:
点击“开始答卷”进行答题
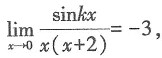 则k的值为______.
则k的值为______.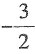
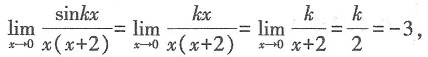 ∴k=-6.故本题选D.
∴k=-6.故本题选D.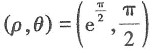 处的切线的直角坐标方程为______.
处的切线的直角坐标方程为______.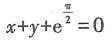
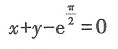
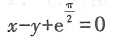
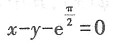

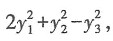 其中P=(e1,e2,e3),若Q=(e1,-e3,e2),则f(x1,x2,x3)在x=Qy下的标准形为______.
其中P=(e1,e2,e3),若Q=(e1,-e3,e2),则f(x1,x2,x3)在x=Qy下的标准形为______.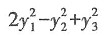
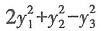
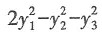
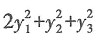
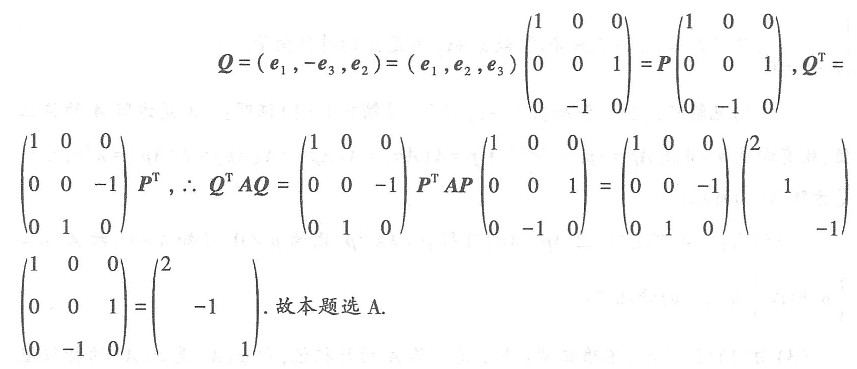
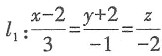 与直线
与直线 的位置关系是______.
的位置关系是______.
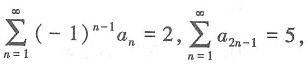 则级数
则级数



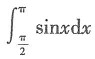 的值为______.
的值为______.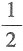
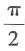
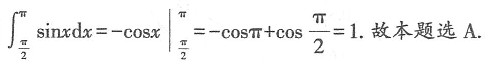
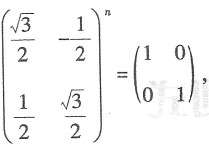 n∈N*,则n的最小值为______.
n∈N*,则n的最小值为______.
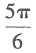
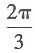
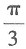
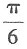
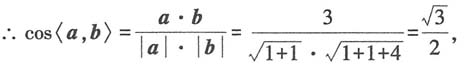 又∵〈a,b〉∈[0,π],∴向量a与b的夹角为
又∵〈a,b〉∈[0,π],∴向量a与b的夹角为 故本题选D.
故本题选D.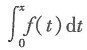
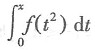
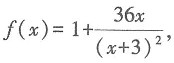 则下列关于曲线f(x)的渐近线的说法正确的是______.
则下列关于曲线f(x)的渐近线的说法正确的是______.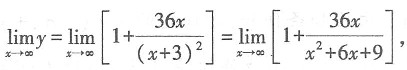 当x→∞时,y→1,所以f(x)的水平渐近线为y=1,f(x)的定义域为x≠-3,当x→-3时,y→∞,则f(x)的垂直渐近线为x=-3.故本题选C.
当x→∞时,y→1,所以f(x)的水平渐近线为y=1,f(x)的定义域为x≠-3,当x→-3时,y→∞,则f(x)的垂直渐近线为x=-3.故本题选C.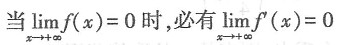
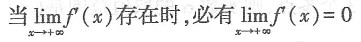
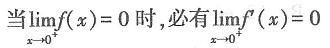

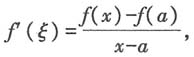 其中ξ∈(a,x),因为f(x)在区间[a,x]
其中ξ∈(a,x),因为f(x)在区间[a,x]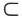 (0,+∞)上有界,所以f(x)-f(a)有界,
(0,+∞)上有界,所以f(x)-f(a)有界,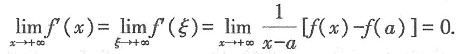 故本题选B.
故本题选B. 是______.
是______.
| 满意程度地区 | 非常满意 | 满意 | 总计 | ||||||||||||||||||||||||||
| A | 30 | 45 | |||||||||||||||||||||||||||
| B | 55 | ||||||||||||||||||||||||||||
| 总计 | 100 | ||||||||||||||||||||||||||||
| 满意程度地区 | 非常满意 | 满意 | 总计 | ||||||||||||||||||||||||||
| A | 30 | 15 | 45 | ||||||||||||||||||||||||||
| B | 35 | 20 | 55 | ||||||||||||||||||||||||||
| 总计 | 65 | 35 | 100 | ||||||||||||||||||||||||||
 所以没有充分的证据判断观众的满意程度与地区有关,可以认为观众的满意程度与地区没有关系.故本题选D.
所以没有充分的证据判断观众的满意程度与地区有关,可以认为观众的满意程度与地区没有关系.故本题选D. 的______.
的______.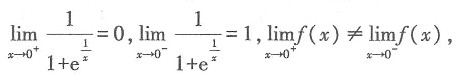 则x=0是函数f(x)的跳跃间断点,故本题选C.
则x=0是函数f(x)的跳跃间断点,故本题选C.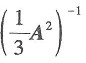 有一个特征值是______.
有一个特征值是______.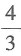

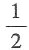
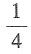
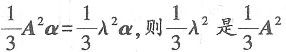 的特征值,由已知λ=2.所以
的特征值,由已知λ=2.所以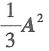 的特征值是
的特征值是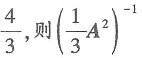 的特征值是
的特征值是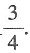 故本题选B.
故本题选B. E为二阶单位矩阵,矩阵B满足BA=B+2E. 则|B|=______.
E为二阶单位矩阵,矩阵B满足BA=B+2E. 则|B|=______.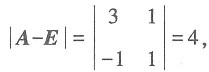 得出|B|=1.故本题选D.
得出|B|=1.故本题选D.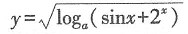
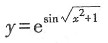
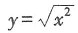
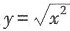 是初等函数,故本题选C.
是初等函数,故本题选C.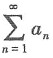 为正项级数,下列结论中正确的是______.
为正项级数,下列结论中正确的是______.
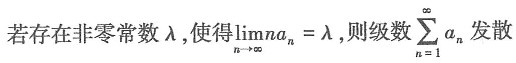
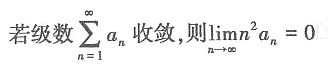

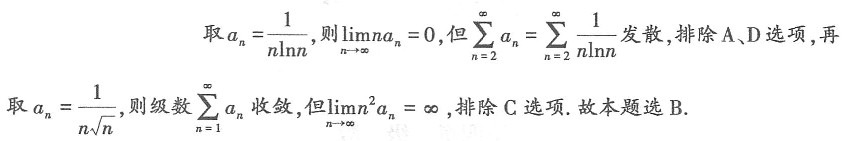
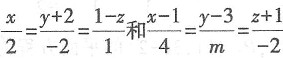 互相垂直,则m=______.
互相垂直,则m=______.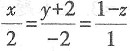 的方向向量为
的方向向量为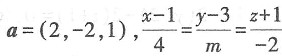 的方向向量为b=(4,m,-2),又两直线相互垂直,所以a·b=0,即2×4+(-2)m+1×(-2)=0,解得m=3.故本题选C.
的方向向量为b=(4,m,-2),又两直线相互垂直,所以a·b=0,即2×4+(-2)m+1×(-2)=0,解得m=3.故本题选C.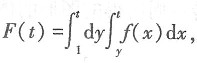 则F'(2)=______.
则F'(2)=______. 于是,F'(t)=f(t)(t-1),从而有F'(2)=f(2).故本题选B.
于是,F'(t)=f(t)(t-1),从而有F'(2)=f(2).故本题选B.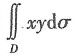 等于______.
等于______.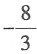
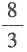
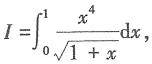 则估计I值的大致范围为______.
则估计I值的大致范围为______.
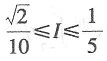
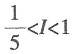

 的值是______.
的值是______.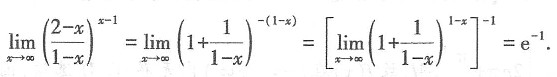
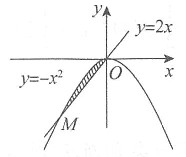
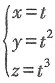 上点M处的切线平行于平面x+2y+z=4,则点M的坐标可以是______.
上点M处的切线平行于平面x+2y+z=4,则点M的坐标可以是______.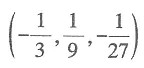
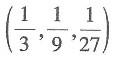
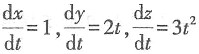 ,故曲线上点M(x,y,z)处切线的方向向量是(1,2t,3t2),而平面x+2y+z=4的方向向量n=(1,2,1),由于切线平行于已知平面,因此s·n=0,即1+4t+3t2=0,解此方程得t=-1或
,故曲线上点M(x,y,z)处切线的方向向量是(1,2t,3t2),而平面x+2y+z=4的方向向量n=(1,2,1),由于切线平行于已知平面,因此s·n=0,即1+4t+3t2=0,解此方程得t=-1或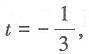 因此点M的坐标可以是
因此点M的坐标可以是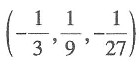 或(-1,1,-1).故本题选B.
或(-1,1,-1).故本题选B.