一、单项选择题1. 设函数z=ln(1+x
2+y
2),当x=1,y=2时,全微分dz是______.
A.
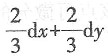
B.dx+dy
C.
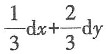
D.
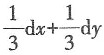
A B C D
C
[考点] 多元函数微分学及其应用
[解析]
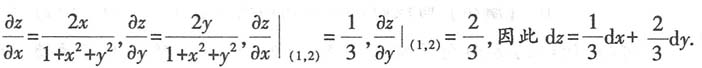
故本题选C.
3. 设f(x)为连续函数,则
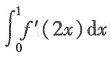
等于______.
A.f(2)-f(0)
B.
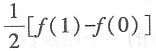
C.
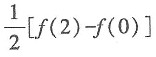
D.f(1)-f(0)
A B C D
C
[考点] 积分
[解析]
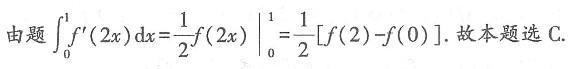
4. 平面
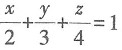
与平面2x+3y-4z=1的位置关系是______.
- A.相交但不垂直
- B.互相垂直
- C.平行但不重合
- D.互相重合
A B C D
A
[考点] 空间线面及其方程
[解析] 平面
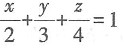
的法向量是
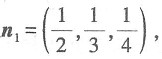
平面2x+3y-4z=1的法向量是n
2=(2,3,-4),所以n
1不平行于n
2,又因为n
1·n
2≠0,可见两个平面的位置关系是相交但不垂直,故本题选A.
5. 已知多项式f(x)=2x
4-7x
3+8x
2+7x-8和g(x)=x
2-3x+4,则f(x)除g(x)的商和余式分别是______.
- A.2x2-x-1和2x+3
- B.2x2-x-3和2x+1
- C.2x2-x-3和2x+4
- D.2x2-x-1和0
A B C D
C
[考点] 行列式
[解析] f(x)=g(x)·(2x
2-x-3)+2x+4,所以
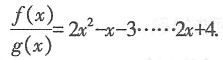
故本题选C
12. 已知
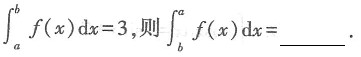
A.
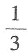
B.-3
C.
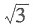
D.0
A B C D
B
[考点] 积分
[解析] 由定积分的性质可知,若
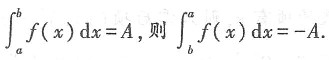
因此
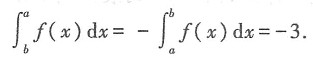
故本题选B.
13. 已知曲线y=x
3+ax
2+2在点x=-1处的切线的斜率为8,则a=______.
A.
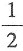
B.
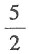
C.

D.
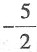
A B C D
D
[考点] 导数与微分
[解析] 由题可知,y'=3x
2+2ax,y'|
x=-1=3-2a=8,解得
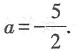
故本题选D.
15. 若级数
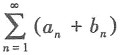
收敛,则______.
A.
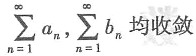
B.

C.
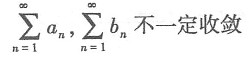
D.
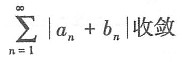
A B C D
C
[考点] 级数
[解析]


16. 二次型
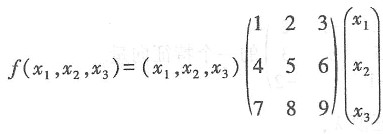
的矩阵为______.
A.
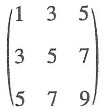
B.
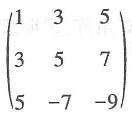
C.

D.
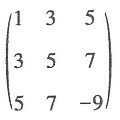
A B C D
A
[考点] 二次型
[解析]


20. 篮子里装有2个红球,3个白球和4个黑球,某人从篮子中随机取出两个球,记事件A为“取出的两个球颜色不同”,事件B为“取出一个红球,一个白球”,则P(B|A)=______.
A.
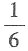
B.
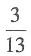
C.
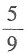
D.
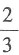
A B C D
B
[考点] 统计与概率
[解析] P(B|A)表示事件A发生的条件下,事件B发生的概率,
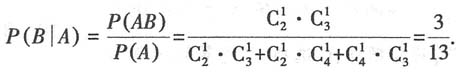
故本题选B.
21. 二次型x
2-xy+y
2是______.
A B C D
A
[考点] 二次型
[解析] 矩阵正定型、负定型、不定型的判定方法有很多种,其中的一种方法为,若二次型对应的矩阵的各阶顺序主子式均大于零,则是正定的;若二次型对应的矩阵的各阶顺序主子式的各阶顺序主子式均小于零,则是负定的;否则,为不定的.设二次型对应矩阵为A.则
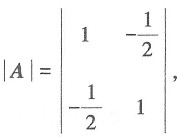
一阶主子式为|1|>0,二阶主子式为
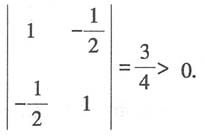
因此此二次型为正定的,故本题选A.
22. 袋子里有形状大小相同的6个球,其中3个白球、2个红球和1个黑球,现请4个人依次从袋子中任意取出一个球,不放回,则第二个人取出红球且第三个人取出白球的概率是______.
A.
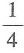
B.
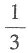
C.
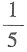
D.
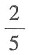
A B C D
C
[考点] 统计与概率
[解析] 若第一个人取得白球,概率为
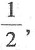
剩余2个白球、2个红球和1个黑球,第二个人取出红球的概率为
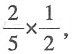
还剩余2个白球、一个红球和一个黑球,第三个人取出白球的概率
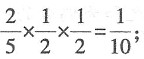
若第一个人取得红球,概率为
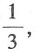
那么第二个人取出红球的概率
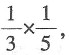
第三个人取出白球的概率
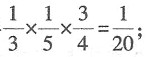
同理若第一个人取出黑球,则第二个人取出红球,第三个人取出白球的概率为
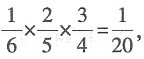
所以第二个人取出红球且第三个人取出白球的概率为
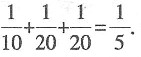
故本题选C.
23. 由曲线
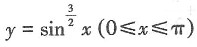
与x轴围成的图形绕x轴旋转所成旋转体的体积为______.
A.
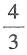
B.

C.
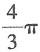
D.
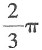
A B C D
C
[考点] 积分
[解析]
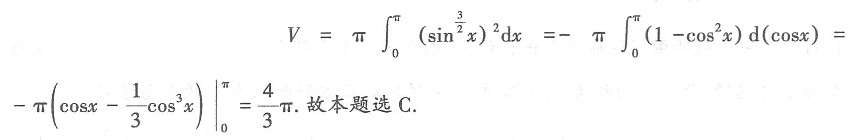
25. 下列各式中,表示(-∞,+∞)上有界函数的是______.
- A.f(x)=xe-|x|
- B.f(x)=xe-x
- C.f(x)=x+sinx
- D.f(x)=x2sinx+1
A B C D
A
[考点] 极限与连续
[解析] 函数有界性:如果在变量x所考虑的范围(用D表示)内,存在一个正数M,使在D上的函数值f(x)都满足|f(x)|≤M,则称函数y=f(x)在D上有界.A选项,根据洛必达法则得,
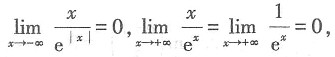
函数有界,故A正确;B选项,
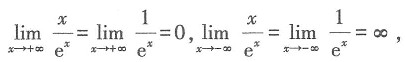
函数无界,故B错误;C选项,

函数无界,故C错误;D选项,

函数无界,故D错误.故本题选A.
27. 设A,B是n阶矩阵,下列结论正确的是______.
A.AB=0
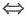
A=0且B=0
B.|A|=0
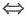
A=0
C.|AB|=0
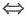
|A|=0或|B|=0
D.A=E
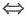
|A|=1
A B C D
C
[考点] 矩阵
[解析]

28. 设n维列向量组α
1,α
2,…,α
m(m<n)线性无关,则n维列向量组β
1,β
2,…,β
m线性无关的充分必要条件为______.
- A.向量组α1,α2,…,αm可由向量组β1,β2,…,βm线性表出
- B.向量组β1,β2,…,βm可由向量组α1,α2,…,αm线性表出
- C.向量组α1,α2,…,αm与向量组β1,β2,…,βm等价
- D.矩阵A=(α1,α2,…,αm)与矩阵B=(β1,β2,…,βm)等价
A B C D
D
[考点] 线性空间与线性变换
[解析] A=(α
1,α
2,…,α
m),B=(β
1,β
2,…,β
m)等价
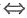
r(α
1,α
2,…,α
m)=r(β
1,β
2,…,β
m)
已知α
1,α
2,…,α
m线性无关时,β
1,β
2,…,β
m线性无关.故本题选D.
29. 设
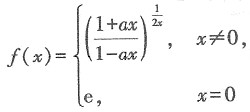
在x=0处连续,则常数a的值为______.
A.1
B.0
C.
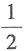
D.e
A B C D
A
[考点] 极限与连续
[解析]

31. 设A是n阶可逆方阵,|A|=3,则|(A
*)
*|=______.
- A.3(n-1)2
- B.3n2-1
- C.3n2-n
- D.3n-1
A B C D
A
[考点] 矩阵
[解析] |A|=3,A可逆,则A
*(A
*)
*=|A
*|E,(A
*)
*=|A
*|(A
*)
-1=
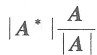
=|A|
n-2A,|(A
*)
*|=||A
n-2A|=|A|
(n-2)n|A|=|A|
n2-2n+1=3
(n-1)2.故本题选A.
32. n维向量组α
1,α
2…,α
s(3≤s≤n)线性无关的充要条件是______.
- A.存在一组全为零的数k1,k2,…,ks,使k1α1+k2α2+…+ksαs=0
- B.α1,α2,…,αs中任意两个向量都线性无关
- C.α1,α2,…,αs中任意一个向量都不能由其余向量线性表示
- D.存在一组不全为零的数k1,k2,…,ks,使k1α1+k2α2+…+ksαs≠0
A B C D
C
[考点] 向量组的线性相关性
[解析] 可用反证法证明.必要性:假设有一向量,如α
s可由α
1,α
2,…,α
s-1线性表示,则α
1,α
2…,α
s线性相关,这和已知矛盾,故任一向量均不能由其余向量线性表示,充分性:假设α
1,α
2,…,α
s线性相关
至少存在一个向量可由其余向量线性表示,这和已知矛盾,故α
1,α
2,…,α
s线性无关.A选项,对任何向量组都有0α
1+0α
2+…+0α
s=0的结论,故A错误;B选项,必要但不充分,如α
1=(1,0,0)
T,α
2= (0,1,0)
T,α
3=(1,1,0)
T,任意两个向量线性无关,但α
1,α
2,α
3线性相关,故B错误;D选项,必要但不充分,如上述的α
1+α
2+α
3≠0,但α
1,α
2,α
3线性相关,故D错误.故本题选C.
33. 下列说法:
①三角形按边分类可分为三边不等的三角形、等腰三角形和等边三角形;
②各条边都相等,各个角都相等的多边形是正多边形;
③面积相等的两个图形是全等图形;
④两边和其中一边的对角对应相等的两个三角形全等;
其中,正确的个数是______.
A B C D
A
[考点] 图形与几何
[解析] 三角形按边分类可分为三边不等的三角形、等腰三角形,故①不符合题意;各条边都相等,各个角都相等的多边形是正多边形,描述正确,故②符合题意;面积相等的两个图形不一定是全等图形,故③不符合题意;两边和其中一边的对角对应相等的两个三角形不一定全等,故④不符合题意.故本题选A.
34. 曲面3x
2+y
2+z
2=12上点M(-1,0,3)处的切平面与平面z=0的夹角是______.
A.
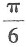
B.
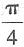
C.
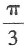
D.
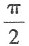
A B C D
B
[考点] 多元函数微分学及其应用
[解析] 设F(x,y,z)=3x
2+y
2+z
2-12,则F'
x(-1,0,3)=-6,F'
y(-1,0,3)=0,F'
z(-1,0,3)=6,曲面在点M处切平面的法向量n
1=(-6,0,6),平面z=0即xOy坐标平面,其法向量可取n
2=(0,0,1),于是切平面与平面z=0的夹角θ的余弦是
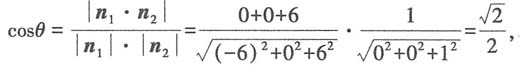
所以

故本题选B.
35. 一袋中放着4个白球和8个黑球,这两种球除了颜色以外没有任何其他区别,从袋中随机摸出1个球,恰好摸出1个白球的概率是______.
A.
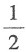
B.
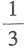
C.
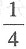
D.
A B C D
B
[考点] 统计与概率
[解析] 袋子中一共有4+8=12(个)球,其中有4个白球,根据概率可知
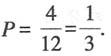
故本题选B.
37. 曲线
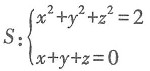
在点(1,-1,0)处的切线方程为______.
A.
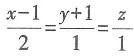
B.
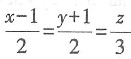
C.
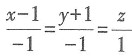
D.

A B C D
D
[考点] 空间线面及其方程
[解析] 曲面x
2+y
2+z
2=2在点(1,-1,0)处的法向量为n
1=(2,-2,0),平面x+y+z=0的法向量为n
2=(1,1,1),于是,曲线
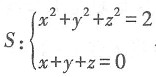
在点(1,-1,0)处的切向量为s=n
1×n
2=(-2,-2,4)=-2(1,1,-2),故所求切线方程为

故本题选D.
39. 下列命题中正确的是______.
- A.若向量组α1,α2,…,αn(n>1)线性相关,则其中每个向量都是其余向量的线性组合
- B.若矩阵A的秩为R(A),则A的所有高于R(A)级的子式(若有的话)全部为零
- C.在全部n(n>1)级排列中,奇排列的个数为n!
- D.等价向量组的秩不一定相等
A B C D
B
[考点] 向量组的线性相关性
[解析] 若向量组α
1,α
2,…,α
n(n>1)线性相关,则其中至少有一个向量能为其余向量的线性组合,A错误;若矩阵A的秩为R(A),则A的所有高于R(A)级的子式(若有的话)所有元素都为0,B正确;在全部n(n>1)级排列中,奇偶排列的个数相等,各有
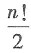
个,C错误;等价向量组的秩一定相等,D错误.故本题选B.
40. 曲线
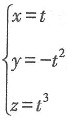
的所有切线中,与平面x+2y+z=-4平行的切线______.
A B C D
B
[考点] 多元函数微分学及其应用
[解析] 曲线的切线方向向量为(x'(t),y'(t),z'(t))=(1,-2t,3t
2),依题意可知,切线的方向向量应与平面x+2y+z=-4的法向量垂直,于是有(1,-2t,3t
2).(1,2,1)=1-4t+3t
2=0,解得
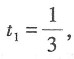
t
2=1,所以与平面x+2y+z=-4平行的切线应有两条.故本题选B.
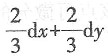
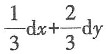
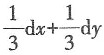
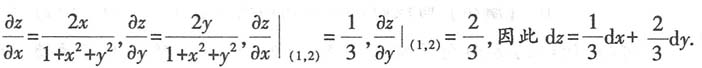
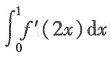 等于______.
等于______.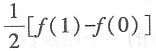
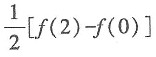
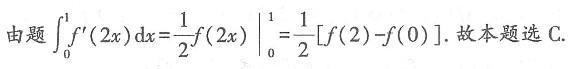
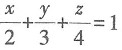 与平面2x+3y-4z=1的位置关系是______.
与平面2x+3y-4z=1的位置关系是______.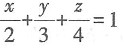 的法向量是
的法向量是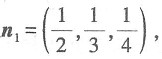 平面2x+3y-4z=1的法向量是n2=(2,3,-4),所以n1不平行于n2,又因为n1·n2≠0,可见两个平面的位置关系是相交但不垂直,故本题选A.
平面2x+3y-4z=1的法向量是n2=(2,3,-4),所以n1不平行于n2,又因为n1·n2≠0,可见两个平面的位置关系是相交但不垂直,故本题选A.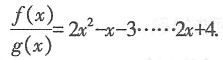 故本题选C
故本题选C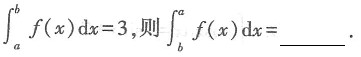
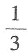
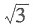
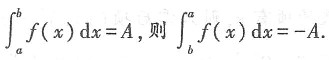 因此
因此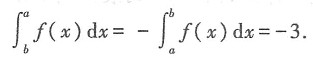 故本题选B.
故本题选B.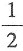
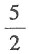

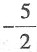
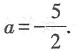 故本题选D.
故本题选D.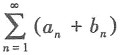 收敛,则______.
收敛,则______.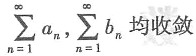

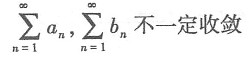
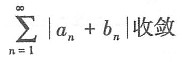


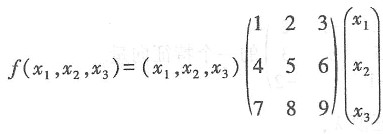 的矩阵为______.
的矩阵为______.
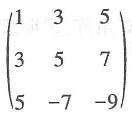




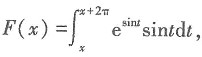 则F(x)______.
则F(x)______. 故本题选A.
故本题选A.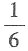
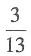
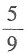
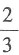
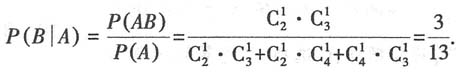 故本题选B.
故本题选B.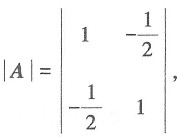 一阶主子式为|1|>0,二阶主子式为
一阶主子式为|1|>0,二阶主子式为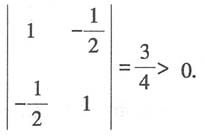 因此此二次型为正定的,故本题选A.
因此此二次型为正定的,故本题选A.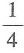
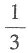
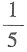
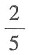
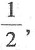 剩余2个白球、2个红球和1个黑球,第二个人取出红球的概率为
剩余2个白球、2个红球和1个黑球,第二个人取出红球的概率为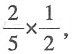 还剩余2个白球、一个红球和一个黑球,第三个人取出白球的概率
还剩余2个白球、一个红球和一个黑球,第三个人取出白球的概率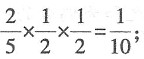 若第一个人取得红球,概率为
若第一个人取得红球,概率为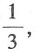 那么第二个人取出红球的概率
那么第二个人取出红球的概率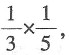 第三个人取出白球的概率
第三个人取出白球的概率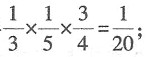 同理若第一个人取出黑球,则第二个人取出红球,第三个人取出白球的概率为
同理若第一个人取出黑球,则第二个人取出红球,第三个人取出白球的概率为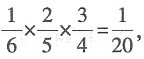 所以第二个人取出红球且第三个人取出白球的概率为
所以第二个人取出红球且第三个人取出白球的概率为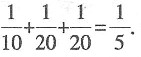 故本题选C.
故本题选C.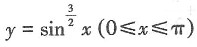 与x轴围成的图形绕x轴旋转所成旋转体的体积为______.
与x轴围成的图形绕x轴旋转所成旋转体的体积为______.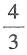

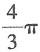
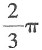
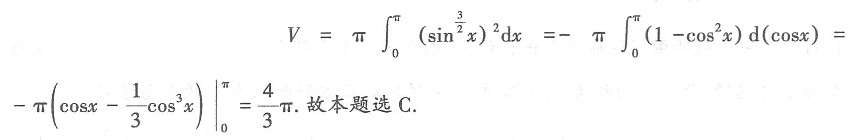
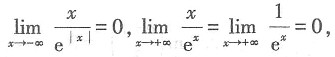 函数有界,故A正确;B选项,
函数有界,故A正确;B选项,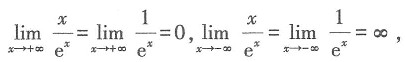 函数无界,故B错误;C选项,
函数无界,故B错误;C选项, 函数无界,故C错误;D选项,
函数无界,故C错误;D选项, 函数无界,故D错误.故本题选A.
函数无界,故D错误.故本题选A.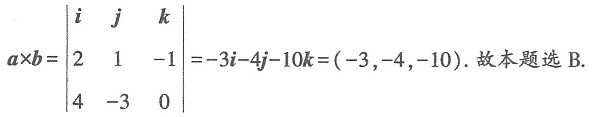
 A=0且B=0
A=0且B=0 A=0
A=0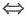 |A|=0或|B|=0
|A|=0或|B|=0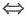 |A|=1
|A|=1
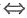 r(α1,α2,…,αm)=r(β1,β2,…,βm)
r(α1,α2,…,αm)=r(β1,β2,…,βm)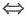 已知α1,α2,…,αm线性无关时,β1,β2,…,βm线性无关.故本题选D.
已知α1,α2,…,αm线性无关时,β1,β2,…,βm线性无关.故本题选D.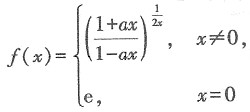 在x=0处连续,则常数a的值为______.
在x=0处连续,则常数a的值为______.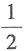

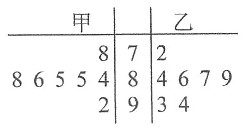
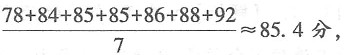 乙成绩的平均数为
乙成绩的平均数为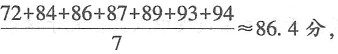 故D选项正确.故本题选D.
故D选项正确.故本题选D.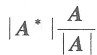 =|A|n-2A,|(A*)*|=||An-2A|=|A|(n-2)n|A|=|A|n2-2n+1=3(n-1)2.故本题选A.
=|A|n-2A,|(A*)*|=||An-2A|=|A|(n-2)n|A|=|A|n2-2n+1=3(n-1)2.故本题选A.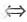 至少存在一个向量可由其余向量线性表示,这和已知矛盾,故α1,α2,…,αs线性无关.A选项,对任何向量组都有0α1+0α2+…+0αs=0的结论,故A错误;B选项,必要但不充分,如α1=(1,0,0)T,α2= (0,1,0)T,α3=(1,1,0)T,任意两个向量线性无关,但α1,α2,α3线性相关,故B错误;D选项,必要但不充分,如上述的α1+α2+α3≠0,但α1,α2,α3线性相关,故D错误.故本题选C.
至少存在一个向量可由其余向量线性表示,这和已知矛盾,故α1,α2,…,αs线性无关.A选项,对任何向量组都有0α1+0α2+…+0αs=0的结论,故A错误;B选项,必要但不充分,如α1=(1,0,0)T,α2= (0,1,0)T,α3=(1,1,0)T,任意两个向量线性无关,但α1,α2,α3线性相关,故B错误;D选项,必要但不充分,如上述的α1+α2+α3≠0,但α1,α2,α3线性相关,故D错误.故本题选C.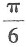
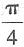
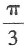
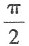
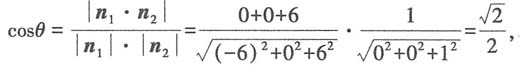 所以
所以 故本题选B.
故本题选B.
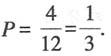 故本题选B.
故本题选B.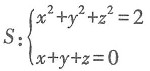 在点(1,-1,0)处的切线方程为______.
在点(1,-1,0)处的切线方程为______.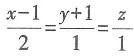
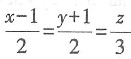
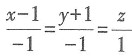

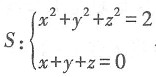 在点(1,-1,0)处的切向量为s=n1×n2=(-2,-2,4)=-2(1,1,-2),故所求切线方程为
在点(1,-1,0)处的切向量为s=n1×n2=(-2,-2,4)=-2(1,1,-2),故所求切线方程为 故本题选D.
故本题选D.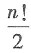 个,C错误;等价向量组的秩一定相等,D错误.故本题选B.
个,C错误;等价向量组的秩一定相等,D错误.故本题选B.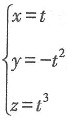 的所有切线中,与平面x+2y+z=-4平行的切线______.
的所有切线中,与平面x+2y+z=-4平行的切线______.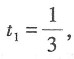 t2=1,所以与平面x+2y+z=-4平行的切线应有两条.故本题选B.
t2=1,所以与平面x+2y+z=-4平行的切线应有两条.故本题选B.