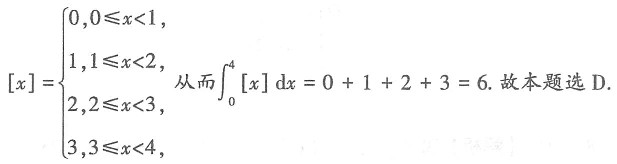一、单项选择题4. 在曲面x
2+y
2+z
2-2x+2y-4z-3=0上,过点(3,-2,4)的切平面方程是______.
- A.2x-y+2z=0
- B.2x-y+2z=16
- C.4x-3y+6z=42
- D.4x-3y+6z=0
A B C D
B
[考点] 多元函数微分学及其应用
[解析] 令F(x,y,z)=x
2+y
2+z
2-2x+2y-4z-3,
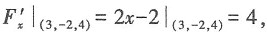
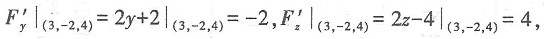
∴过点(3,-2,4)的切平面方程为4(x-3)-2(y+2)+4(z-4)=0,即2x-y+2z=16.故本题选B.
5. 当x>0时,
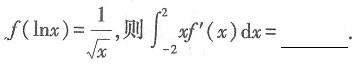
A.
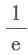
B.
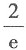
C.
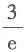
D.
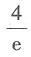
A B C D
D
[考点] 积分
[解析]

6. 对于级数
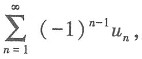
其中u
n>0(n=1,2,3,…),则下列命题中正确的是______.
A.

B.
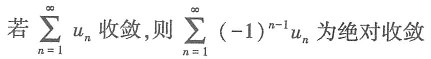
C.
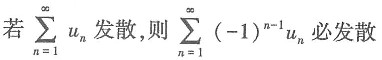
D.

A B C D
B
[考点] 级数
[解析]
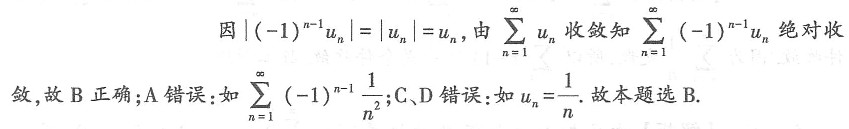
7. 已知α
1=(-1,1,a,4)
T,α
2=(-2,1,5,a)
T,α
3= (a,2,10,1)
T,是4阶方阵A的3个不同特征值对应的特征向量,则a的取值为______.
- A.a≠5
- B.a≠4
- C.a≠-3
- D.a≠-3且a≠4
A B C D
A
[考点] 方阵的特征值与特征向量
[解析] α
1,α
2,α
3是三个不同特征值的特征向量,必线性无关,由
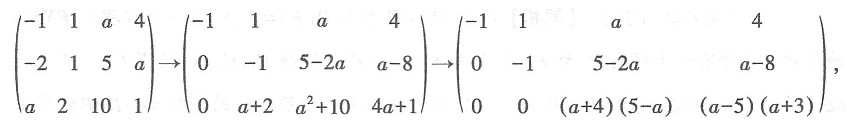
知a≠5.故本题选A.
8. 已知向量组α
1,α
2,α
3,α
4线性无关,则向量组______.
- A.α1-α2,α2-α3,α3-α4,α4-α1线性无关
- B.α1+α2,α2+α3,α3+α4,α4+α1线性无关
- C.α1+α2,α2+α3,α3+α4,α4-α1线性无关
- D.α1+α2,α2+α3,α3-α4,α4-α1线性无关
A B C D
C
[考点] 向量组的线性相关性
[解析]

因此
r(α
1+α
2,α
2 +α
3,α
3+α
4,α
4-α
1)=r(α
1,α
2,α
3,α
4)=4,故向量组α
1+α
2,α
2+α
3,α
3+α
4,α
4-α
1,线性无关,故C正确;对于其余选项中的向量组,可以通过类似的方法判断线性相关性,也可以通过观察法予以排除,如(α
1-α
2)+(α
2-α
3)+(α
3-α
4)+(α
4-α
1)=0,故A错误;如(α
1+α
2)-(α
2+α
3)+(α
3+α
4)-(α
4+α
1)=0,故B错误;(α
1+α
2)-(α
2+α
3)+(α
3-α
4)+(α
4-α
1)=0,故D错误.故本题选C.
9. 已知f(X)=∫(x+e
x)dx,则f'(x)=______.
A.x+e
x B.x
2+e
x C.
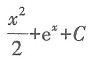
D.x+e
x+C
A B C D
A
[考点] 积分
[解析] 根据不定积分与求导的关系,若一个函数先进行不定积分,后求导,将还原为原来的函数,故正确答案为A项,注意:若对一个函数先求导,后进行不定积分,则结果应为原来的函数加上一个常数,故本题选A.
11. 某中等职业学校旅游专业现有9名技能大赛选手,其中5名男生、4名女生,现要从这9名选手中任选4名参加技能大赛,则恰好选到男女生各2名的概率是______.
A.
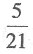
B.
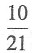
C.
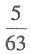
D.
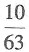
A B C D
B
[考点] 统计与概率
[解析] 从这9名选手中任选4名,则有
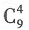
种选法;从这9名选手中选4名,恰好选到男女生各2名,则有
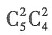
种选法.所以恰好选到男女生各2名的概率是
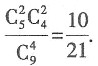
故本题选B.
13. 分别从集合M={1,2,3}和集合N={4,5,6}中各取一个数,则这两个数之和为偶数的概率为______.
A.
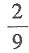
B.
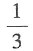
C.
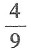
D.
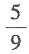
A B C D
C
[考点] 统计与概率
[解析] 两个集合中各选一个数,共有3×3=9(种)可能,两数之和为偶数的情况有1和5,2和4,2和6,3和5,共4种可能,所以两数之和为偶数的概率是
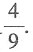
故本题选C.
14. 函数
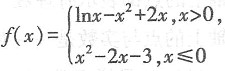
的零点个数为______.
A B C D
C
[考点] 数与代数
[解析] 当x>0时f(x)=0
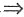
lnx=x
2-2x,则函数f(x)的零点个数为函数y=lnx与函数y=x
2-2x,x∈(0,+∞)的交点个数,作出两个函数的图象如下图所示,
由图可知,当x>0时,函数f(x)的零点有两个,当x≤0时,f(x)=x
2-2x-3=0,可得x=-1或x=3(舍去),即当x≤0时,函数f(x)的零点有一个;综上,函数f(x)的零点有三个,故本题选C.
17. 当x→0时,函数e
x-cosx是x
2的______.
- A.低阶无穷小量
- B.等价无穷小量
- C.高阶无穷小量
- D.同阶但非等价的无穷小量
A B C D
A
[考点] 极限与连续
[解析] 根据洛必达法则,
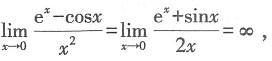
所以当x→0时,函数e
x-cosx是比x
2低阶的无穷小.故本题选A.
18. 设A=(α
1,α
2,α
3,α
4)是4阶矩阵,A
*为A的伴随矩阵,若(1,0,1,0)
T是方程组Ax=0的一个基础解系,则A
*x=0基础解系可为______.
- A.α1,α3
- B.α1,α2
- C.α1,α2,α3
- D.α2,α3,α4
A B C D
D
[考点] 线性方程组
[解析] 由Ax=0的基础解系只有一个知R(A)=3,所以R(A
*)=1,又由A
*A=|A|E=0知,α
1,α
2,α
3,α
4都是A
*x=0的解,且A
*x=0的极大线性无关组就是其基础解系,又
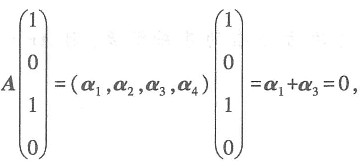
所以α
1,α
3线性相关,故α
1,α
2,α
4或α
2,α
3,α
4为极大无关组.故本题选D.
20. 设f(x,y)连续,且
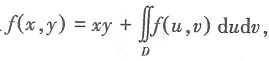
其中D是由y=0,y=x
2,x=1所围区域,则f(x,y)=______.
A.xy
B.2xy
C.
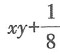
D.xy+1
A B C D
C
[考点] 积分
[解析]
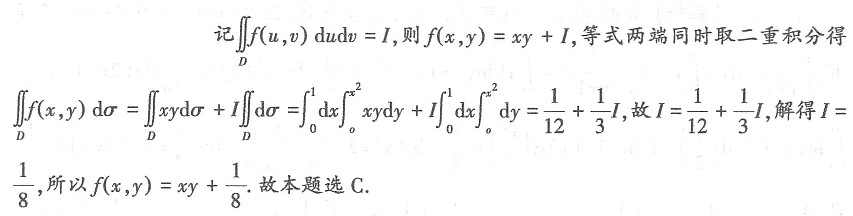
22. 当x→0时,下列哪个函数是无穷小?______
A.y=cosx
B.y=x
2+1
C.y=x·sinx
D.

A B C D
C
[考点] 极限与连续
[解析] 当x→0时,A选项,y=cosx趋向于1;B选项,y=x
2+1趋向于1;C选项,y=x·sinx趋向于0;D选项,
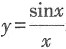
趋向于1.故本题选C.
25. 在
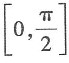
上的曲线y=sinx绕x轴旋转一周所得的图形的体积为______.
A.
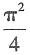
B.
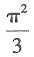
C.
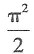
D.π
2 A B C D
A
[考点] 积分
[解析] 设所得旋转体的体积为V,则
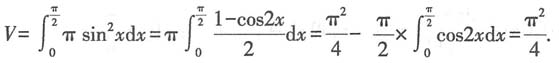
故本题选A.
26. 设数列x
n,y
n满足
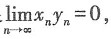
则下列判断正确的是______.
A.若x
n发散,则y
n必发散
B.若x
n无界,则y
n必有界
C.若x
n有界,则y
n必为无穷小
D.若
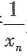
为无穷小,则y
n必为无穷小
A B C D
D
[考点] 极限与连续
[解析] A,B选项显然不对,若x
n有界,且y
n为无穷小,则
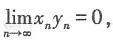
反之不一定,故C选项错;排除法可知D选项正确,因为
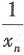
为无穷小.则
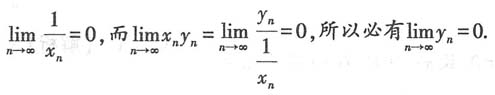
故本题选D.
27. 已知3阶矩阵A有λ
1=1,λ
2=2,λ
3=3,则2A
*的特征值是______.
- A.1,2,3
- B.4,6,12
- C.2,4,6
- D.8,16,24
A B C D
B
[考点] 方阵的特征值与特征向量
[解析] 2A
*的特征值是
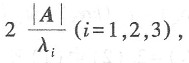
其中|A|=λ
1λ
2λ
3,λ
i(i=1,2,3)是A的特征值,分别为1,2,3,故2A
*的特征值为4,6,12.故本题选B.
30. 直线
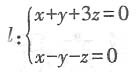
与平面x-y+2z+1=0的夹角θ是______.
A.
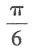
B.
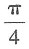
C.
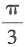
D.
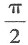
A B C D
A
[考点] 空间线面及其方程
[解析]

31. 如果当x→0时,
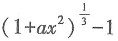
与cosx-1是等价无穷小,则常数a的值为______.
A.-1
B.
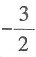
C.-2
D.-3
A B C D
B
[考点] 极限与连续
[解析] 根据题意得,
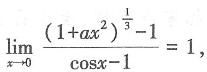
则根据等价无穷小替换得
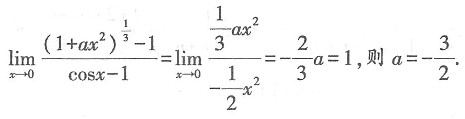
故本题选B.
34. 方程(x
2-2x+3)
2=4x
2-8x+17的实数根的个数为______.
A B C D
B
[考点] 数与代数
[解析] (x
2-2x+3)
2=4x
2-8x+17,(x
2-2x+3)
2=4x
2-8x+12+5,(x
2-2x+3)
2=4(x
2-2x+3)+5,(x
2-2x+3)
2-4(x
2-2x+3)-5=0,(x
2-2x+3-5)(x
2-2x+3+1)=0,解得x
2-2x+3-5=0或x
2-2x+3+1=0.解方程x
2-2x-2=0得,
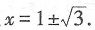
方程x
2-2x+4=0的Δ<0,无实数根.所以方程(x
2-2x+3)
2=4x
2-8x+17的实数根的个数为2.故本题选B.
35. 二次型x
2-3xy+y
2是______.
A B C D
C
[考点] 二次型
[解析] 该二次型对应的系数矩阵为
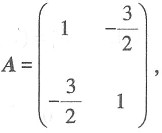
可得其一阶顺序主子式为|1|>0,二阶顺序主子式为

故本题选C.
36. 设向量x与向量a=2i-j+3k平行,且满足方程a·x=7,则向量x=______.
A.
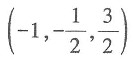
B.

C.
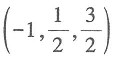
D.

A B C D
B
[考点] 空间向量
[解析] 设x=(x
1,x
2,x
3),由x//a得
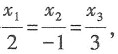
由a·x=7得2x
1-x
2+3x
3=7,解得
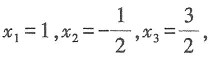
所以
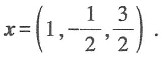
故本题选B.
37. 设f(x)为可导函数,且满足条件
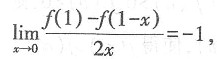
则曲线y=f(x)在点(1,f(1))处的切线斜率为______.
A.2
B.-1
C.
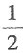
D.-2
A B C D
D
[考点] 导数与微分
[解析]
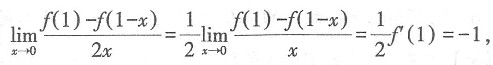
则f'(1)=-2,而曲线y=f(x)在点(1,f(1))处的斜率为f'(1)=-2.故本题选D.
 则______.
则______.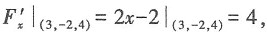
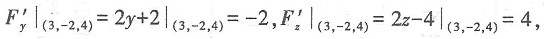 ∴过点(3,-2,4)的切平面方程为4(x-3)-2(y+2)+4(z-4)=0,即2x-y+2z=16.故本题选B.
∴过点(3,-2,4)的切平面方程为4(x-3)-2(y+2)+4(z-4)=0,即2x-y+2z=16.故本题选B.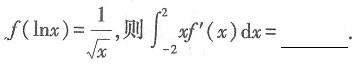
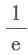
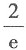
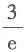
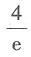

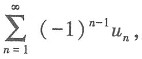 其中un>0(n=1,2,3,…),则下列命题中正确的是______.
其中un>0(n=1,2,3,…),则下列命题中正确的是______.
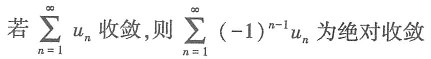
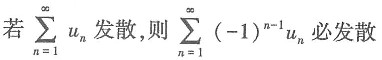

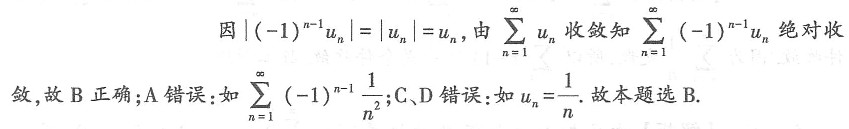
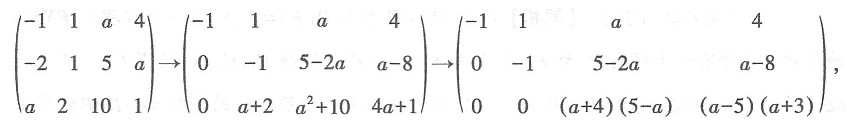 知a≠5.故本题选A.
知a≠5.故本题选A.
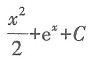
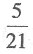
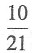
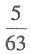
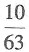
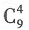 种选法;从这9名选手中选4名,恰好选到男女生各2名,则有
种选法;从这9名选手中选4名,恰好选到男女生各2名,则有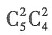 种选法.所以恰好选到男女生各2名的概率是
种选法.所以恰好选到男女生各2名的概率是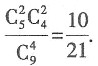 故本题选B.
故本题选B.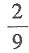
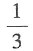
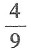
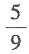
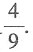 故本题选C.
故本题选C.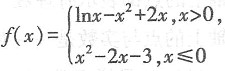 的零点个数为______.
的零点个数为______.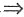 lnx=x2-2x,则函数f(x)的零点个数为函数y=lnx与函数y=x2-2x,x∈(0,+∞)的交点个数,作出两个函数的图象如下图所示,
lnx=x2-2x,则函数f(x)的零点个数为函数y=lnx与函数y=x2-2x,x∈(0,+∞)的交点个数,作出两个函数的图象如下图所示,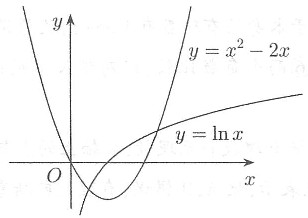
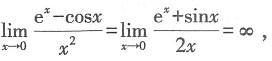 所以当x→0时,函数ex-cosx是比x2低阶的无穷小.故本题选A.
所以当x→0时,函数ex-cosx是比x2低阶的无穷小.故本题选A.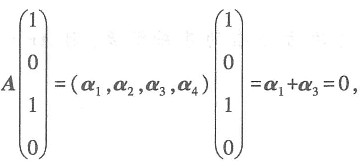 所以α1,α3线性相关,故α1,α2,α4或α2,α3,α4为极大无关组.故本题选D.
所以α1,α3线性相关,故α1,α2,α4或α2,α3,α4为极大无关组.故本题选D.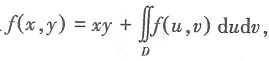 其中D是由y=0,y=x2,x=1所围区域,则f(x,y)=______.
其中D是由y=0,y=x2,x=1所围区域,则f(x,y)=______.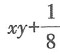
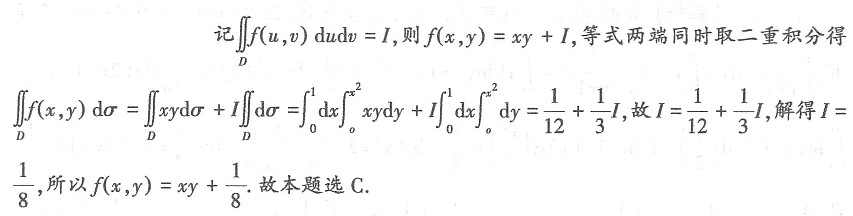

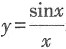 趋向于1.故本题选C.
趋向于1.故本题选C. 的定义域是______.
的定义域是______.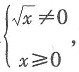 可得x>0,令arcsiny=φ,y=sinφ,∴-1≤y≤1.故本题选D.
可得x>0,令arcsiny=φ,y=sinφ,∴-1≤y≤1.故本题选D.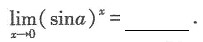
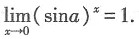
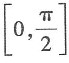 上的曲线y=sinx绕x轴旋转一周所得的图形的体积为______.
上的曲线y=sinx绕x轴旋转一周所得的图形的体积为______.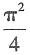
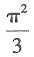
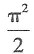
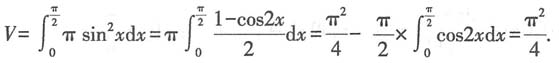 故本题选A.
故本题选A.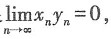 则下列判断正确的是______.
则下列判断正确的是______.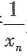 为无穷小,则yn必为无穷小
为无穷小,则yn必为无穷小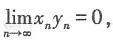 反之不一定,故C选项错;排除法可知D选项正确,因为
反之不一定,故C选项错;排除法可知D选项正确,因为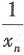 为无穷小.则
为无穷小.则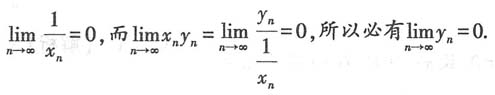 故本题选D.
故本题选D.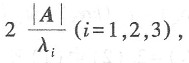 其中|A|=λ1λ2λ3,λi(i=1,2,3)是A的特征值,分别为1,2,3,故2A*的特征值为4,6,12.故本题选B.
其中|A|=λ1λ2λ3,λi(i=1,2,3)是A的特征值,分别为1,2,3,故2A*的特征值为4,6,12.故本题选B. x∈R,f'(-x)=f'(x),所以g(x)=f'(x)为偶函数,可得g(x)在关于原点对称区间上的单调性相反.故本题选A.
x∈R,f'(-x)=f'(x),所以g(x)=f'(x)为偶函数,可得g(x)在关于原点对称区间上的单调性相反.故本题选A. 则第四行各元素余子式之和的值为______.
则第四行各元素余子式之和的值为______.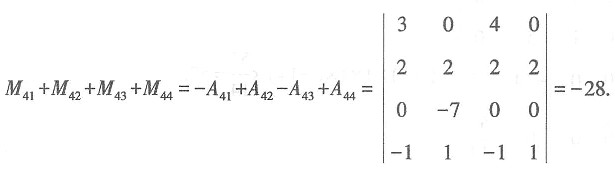 故本题选A.
故本题选A.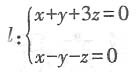 与平面x-y+2z+1=0的夹角θ是______.
与平面x-y+2z+1=0的夹角θ是______.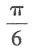
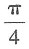
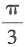
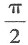

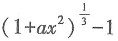 与cosx-1是等价无穷小,则常数a的值为______.
与cosx-1是等价无穷小,则常数a的值为______.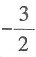
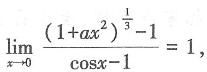 则根据等价无穷小替换得
则根据等价无穷小替换得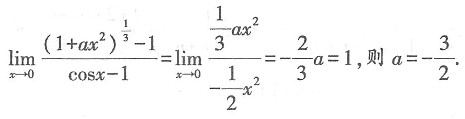 故本题选B.
故本题选B.



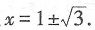 方程x2-2x+4=0的Δ<0,无实数根.所以方程(x2-2x+3)2=4x2-8x+17的实数根的个数为2.故本题选B.
方程x2-2x+4=0的Δ<0,无实数根.所以方程(x2-2x+3)2=4x2-8x+17的实数根的个数为2.故本题选B. 可得其一阶顺序主子式为|1|>0,二阶顺序主子式为
可得其一阶顺序主子式为|1|>0,二阶顺序主子式为 故本题选C.
故本题选C.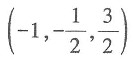

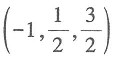

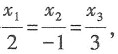 由a·x=7得2x1-x2+3x3=7,解得
由a·x=7得2x1-x2+3x3=7,解得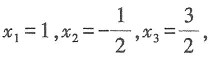 所以
所以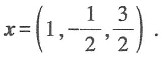 故本题选B.
故本题选B.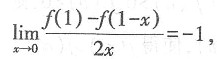 则曲线y=f(x)在点(1,f(1))处的切线斜率为______.
则曲线y=f(x)在点(1,f(1))处的切线斜率为______.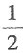
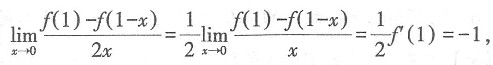 则f'(1)=-2,而曲线y=f(x)在点(1,f(1))处的斜率为f'(1)=-2.故本题选D.
则f'(1)=-2,而曲线y=f(x)在点(1,f(1))处的斜率为f'(1)=-2.故本题选D.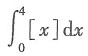 的值为______.
的值为______.