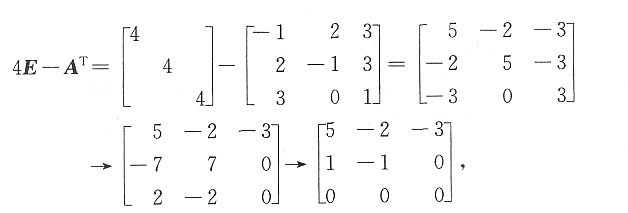一、选择题下列每题给出的四个选项中,只有一个选项是符合题目要求的.1. 设f(x)∈[0,1],在(0,1)内可导,且f(0)=f(1)=0,
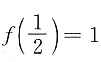
,则______
A.存在ξ∈
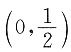
使f(ξ)=ξ.
B.不存在ξ∈

使f(ξ)=ξ.
C.存在ξ∈

使f(ξ)=ξ.
D.不存在ξ∈
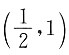
使f(ξ)=ξ.
A B C D
C
[解析] 设辅助函数φ(x)=f(x)-x,则
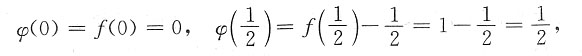
φ(1)=f(1)-1=0-1=-1.
由介值定理知,存在
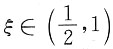
使得f(ξ)=ξ.
2. 设δ>0,f(x)在[-δ,δ]上有定义,f(0)=1,且满足

,则函数f(x)在x=0点处______
A.可微,且f
'(0)=-1.
B.可微,且
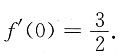
C.可微,且f
'(0)=1.
D.不可微.
A B C D
B
[解析]
思路一: 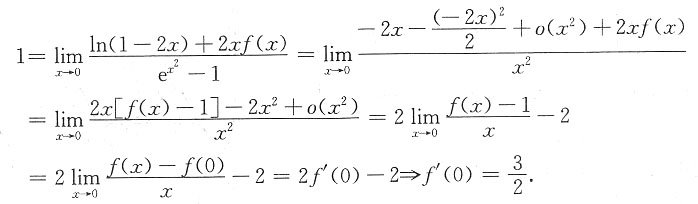 思路二:
思路二: 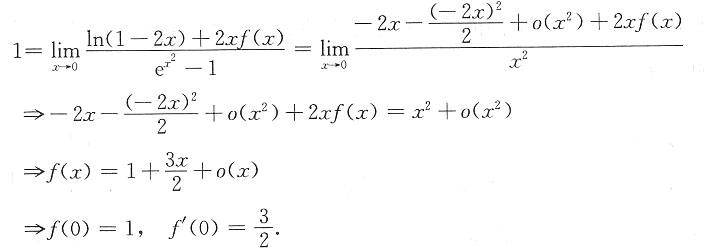
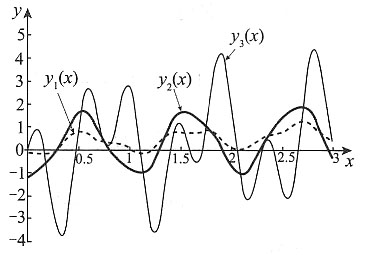
4. 下图中的三条曲线分别是f(x)、
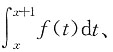
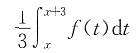
的图形,按此顺序,它们与图中所标示y
1(x),y
2(x),y
3(x)的对应关系是______
- A.y1(x),y2(x),y3(x).
- B.y1(x),y3(x),y2(x).
- C.y3(x),y1(x),y2(x).
- D.y3(x),y2(x),y1(x).
A B C D
D
[解析]
思路一:因为定积分
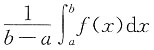
表示函数在区间上的平均值,而一个函数通过移动平均后,其相应曲线的起伏变化会变小,也就是曲线被抹平滑了,而且平均的区间越长,抹平滑的效果越好.这是定积分的重要性质,而该题三个函数中的两个是用积分表示的函数,正是在两个长度不同区间上的滑动平均值,即
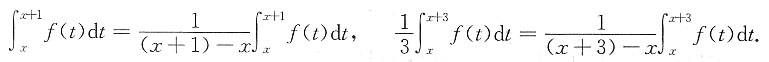
因为起伏变化最大的是y
3(x),其次是y
2(x),起伏最小的是y
1(x),故可以判断解答的次序是y
3(x),y
2(x),y
1(x).
思路二:也可以利用变限定积分与被积函数的关系,通过图上的特殊点来判断.
起伏变化最大的是y
3(x),试设y
3(x)=f(x),则
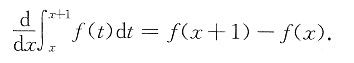
由此可知
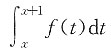
的极值点x
*满足条件
f(x
*+1)=f(x
*),
图中只有y
2(x)满足此性质.同样,
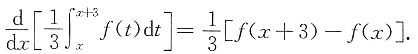
由此可知,
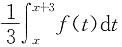
的极值点x
*满足条件f(x
*+3)=f(x
*),图中只有y
1(x)满足此性质.
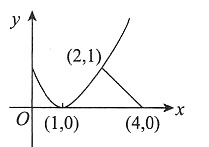
5. 在曲线y=(x-1)
2上点(2,1)处引该曲线的法线,由该法线、x轴及该曲线围成的区域为D,则D绕x轴旋转一周生成的旋转体的体积为______
A.π.
B.
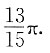
C.
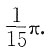
D.
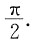
A B C D
B
[解析] y
'=2(x-1),则(2,1)处法线斜率
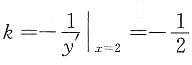
,法线方程为
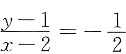
,即
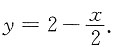
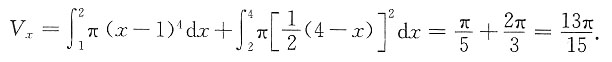
6. 已知

其中g(x)在x=0的某邻域内具有二阶导数,且g(0)=0,则f(x)______
A.在x=0处连续,但不可导.
B.在x=0处可导,且f
'(0)=-g
"(0).
C.在x=0处可导,且
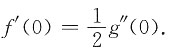
D.在x=0处可导,且f(0)=g
"(0).
A B C D
C
[解析]
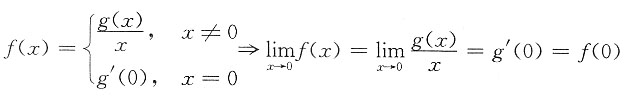
,
f(x)在x=0点处连续.x≠0,
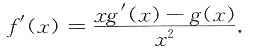
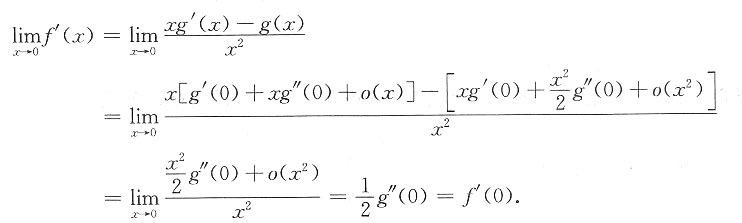
或者
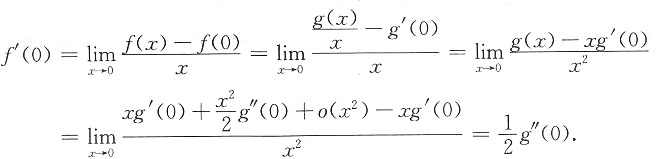
7. 由直线y=-1,x=-1,x=1,及半圆
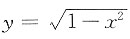
所围成的平面图形的形心坐标为______
A.
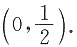
B.
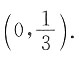
C.(0,1).
D.
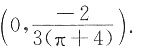
A B C D
D
[解析] 由对称性知

.把平面图形分成D
1,D
2两部分

故
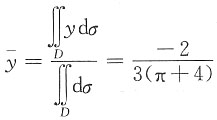
,所以形心坐标为
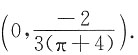
9. 设
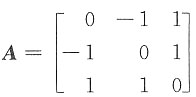
,则当kE+A是正定矩阵时,k应满足条件______
- A.k>-1.
- B.k>2.
- C.-1<k<2.
- D.k任意.
A B C D
B
[解析]
思路一:
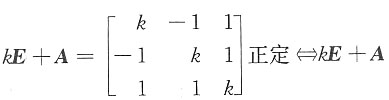
的全部顺序主子式大于零.
D
1=k>0,
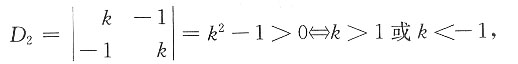
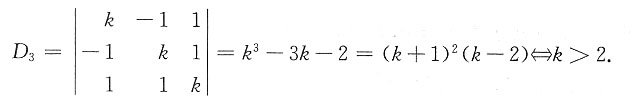
取公共部分,知k+A正定
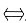
k>2.
思路二:kE+A正定
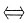
kE+A的特征值全部大于零,A的特征多项式为
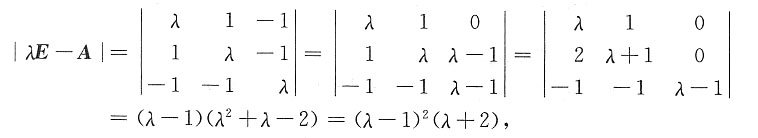
A有特征值λ
1=λ
2=1,λ
3=-2,kE+A有特征值k+1(二重)和k-2.
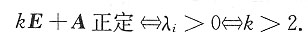
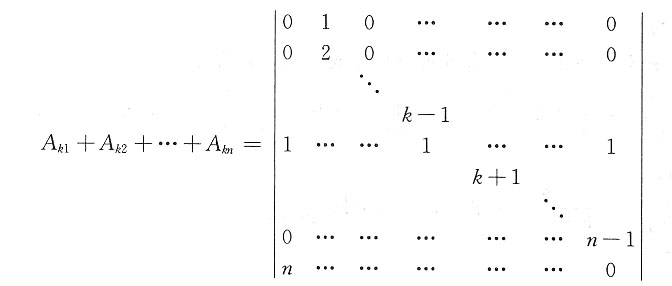
10. 已知n阶矩阵
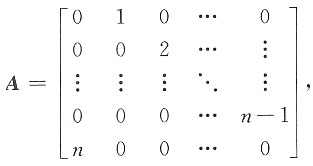
则|A|中第k行元素代数余子式之和A
k1+A
k2+…A
kn=______
A.k!
B.
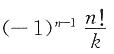
C.n!
D.(-1)
n-1·k!
A B C D
B
[解析] 由按行展开定理

三、解答题本题共70分.解答应写出文字说明、证明过程或演算步骤.1. 计算不定积分
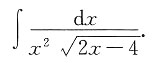
思路一: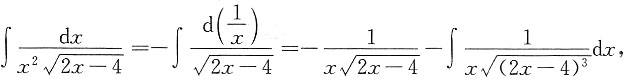
对第二项取变换
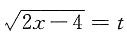
,则
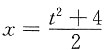
,dx=tdt,于是
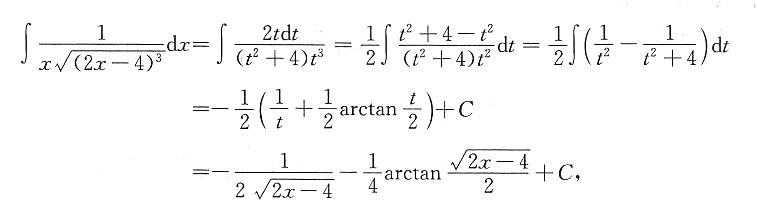
因此
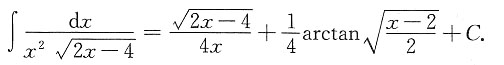 思路二
思路二:令
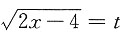
,则
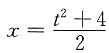
,dx=tdt,于是
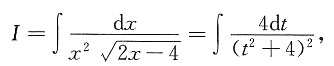
再令t=2tanu,dt=2sec
2udu,则
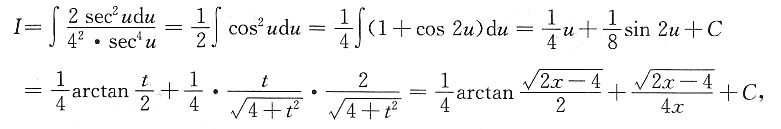
因此

2. 若f(x)在(-∞,+∞)内有二阶连续导数,证明对任意的a<c<b,都存在ξ∈(a,b),使得
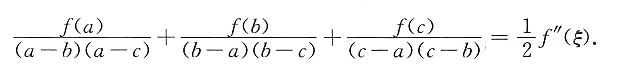
证:
思路一:因为
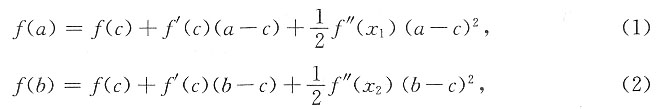
所以(c-a)×式(2)+(b-c)×式(1)得
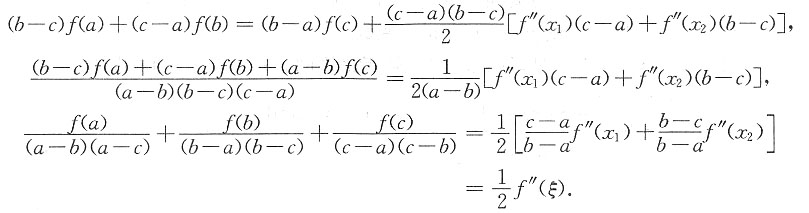
注:用到了二阶导函数f
"(x)的介值性质.
思路二:记
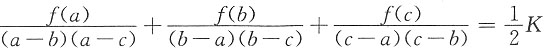
,则
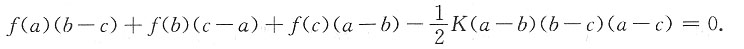
设辅助函数
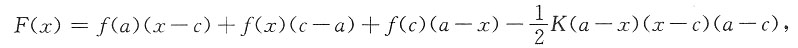
则F(a)=F(b)=F(c)=0,所以存在ξ∈(a,b),使得f
"(ξ)=0,即
f
"(ξ)(c-a)+K(a-c)=0.
故K=f
"(ξ).
思路三:设辅助函数
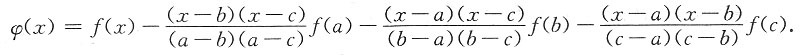
由φ(a)=φ(b)=φ(c)=0,可知
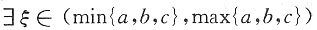
,使
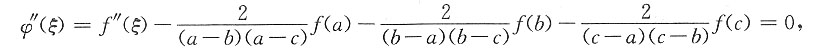
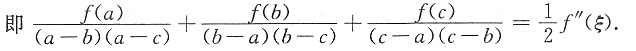
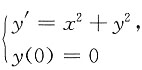 的唯一解.
的唯一解.3. 若
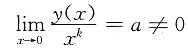
,求常数k和a的值;
4. 证明函数y=y(x)的图形关于原点(0,0)对称;
设φ(x)=-y(-x),可以证明φ(x)也是题设初值问题的解.
首先有φ(0)=-y(-0)=-y(0)=0,又
φ'(x)=-y'(-x)×(-1)=y'(-x),
x2+φ2(x)=x2+[-y(-x)]2=(-x)2+y2(-x)=y'(-x).
所以,φ'(x)=x2+φ2(x).
因此,φ(x)也是题设初值问题的解,由于其解是唯一的,所以φ(x)=-y(-x),即
y(x)=-y(-x),则y=y(x)是奇函数.
5. 作y=y(x)的图形.
由于y=y(x)是奇函数,今只需考虑区间x∈[0,+∞)的图形:
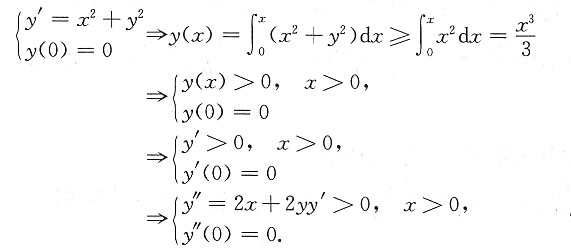
可见,当x∈(0,+∞)时,y=y(x)严格递增,严格向上凹,在曲线
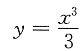
之上,函数图形如下图所示.
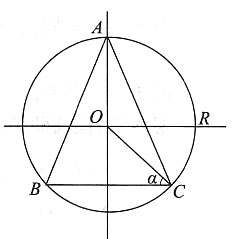
6. 在半径为R的球内作内接正圆锥体,试求其最大体积.
如下图所示,设圆半径OC与内接正圆锥底直径BC的夹角为α,则内接正圆锥的底面半径为
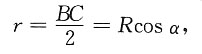
高为h=R(1+sinα),其中
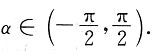
内接正圆锥的体积为
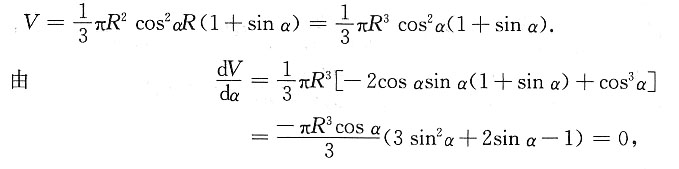
得
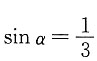
.故当内接正圆锥的底面直径为
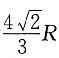
、高为
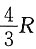
时,其体积最大,最大体积为
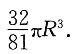
7. 设D={(x,y)|xy≥4,x+y≤5},求
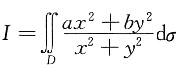
的值.
8. 设
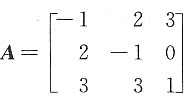
,有特征向量ξ=[1,-2,1]
T,求A的对应于特征向量ξ的特征值λ.A
T有特征值μ=4,求A
T对应特征值μ=4的特征向量.
因
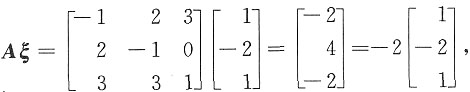
故A对应于ξ的特征值为λ=-2.
又
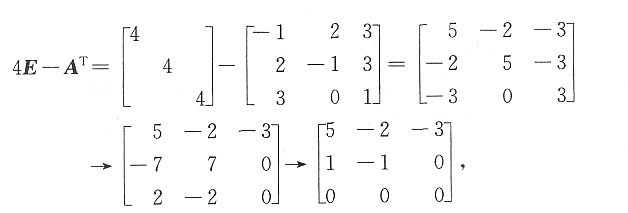
则(4E-A
T)x=0有解η=[1,1,1]
T.
故A
T对应于特征值μ=4的全部特征向量为k[1,1,1]
T,其中k是任意非零常数.
9. 设A是n阶实矩阵,有特征值λ,对应的特征向量为ξ,A
T有特征值μ,其中μ≠λ对应的特征向量为η,证明ξ,η正交.
由题设Aξ=λξ,ATη=μη.将Aξ=λξ两边转置,得ξTAT=λξT,再两边右乘η,
得 ξTATη=ξTμη=μξTη=λξTη,
(λ-μ)ξTη=0,
又μ≠λ,得证ξTη=0,即ξ,η正交.
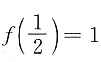 ,则______
,则______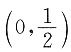 使f(ξ)=ξ.
使f(ξ)=ξ. 使f(ξ)=ξ.
使f(ξ)=ξ. 使f(ξ)=ξ.
使f(ξ)=ξ.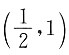 使f(ξ)=ξ.
使f(ξ)=ξ.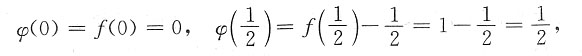
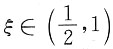 使得f(ξ)=ξ.
使得f(ξ)=ξ. ,则函数f(x)在x=0点处______
,则函数f(x)在x=0点处______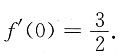
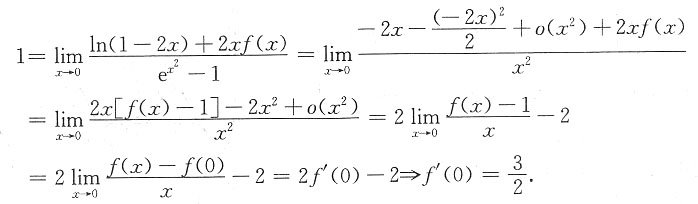
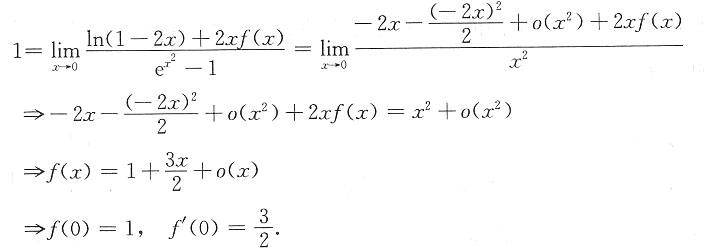
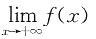 存在,
存在, 则______
则______
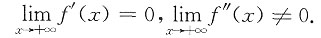
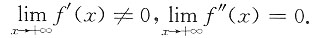
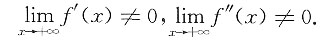


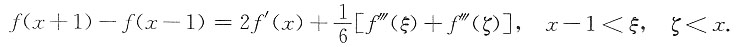
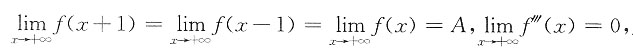 所以
所以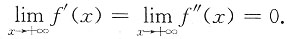
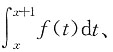
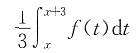 的图形,按此顺序,它们与图中所标示y1(x),y2(x),y3(x)的对应关系是______
的图形,按此顺序,它们与图中所标示y1(x),y2(x),y3(x)的对应关系是______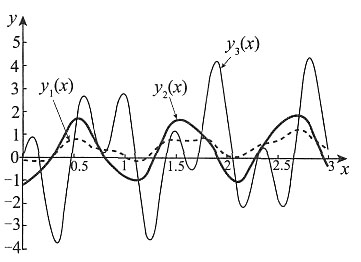
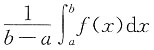 表示函数在区间上的平均值,而一个函数通过移动平均后,其相应曲线的起伏变化会变小,也就是曲线被抹平滑了,而且平均的区间越长,抹平滑的效果越好.这是定积分的重要性质,而该题三个函数中的两个是用积分表示的函数,正是在两个长度不同区间上的滑动平均值,即
表示函数在区间上的平均值,而一个函数通过移动平均后,其相应曲线的起伏变化会变小,也就是曲线被抹平滑了,而且平均的区间越长,抹平滑的效果越好.这是定积分的重要性质,而该题三个函数中的两个是用积分表示的函数,正是在两个长度不同区间上的滑动平均值,即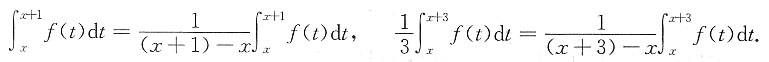
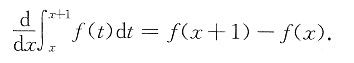
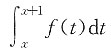 的极值点x*满足条件
的极值点x*满足条件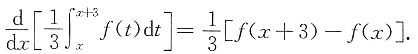
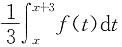 的极值点x*满足条件f(x*+3)=f(x*),图中只有y1(x)满足此性质.
的极值点x*满足条件f(x*+3)=f(x*),图中只有y1(x)满足此性质.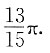
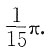
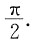
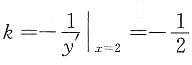 ,法线方程为
,法线方程为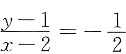 ,即
,即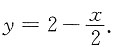
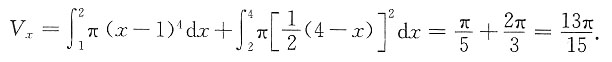
 其中g(x)在x=0的某邻域内具有二阶导数,且g(0)=0,则f(x)______
其中g(x)在x=0的某邻域内具有二阶导数,且g(0)=0,则f(x)______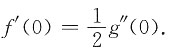
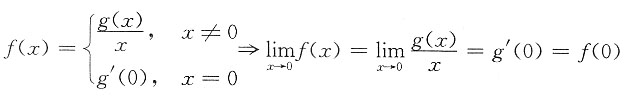 ,
,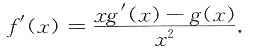
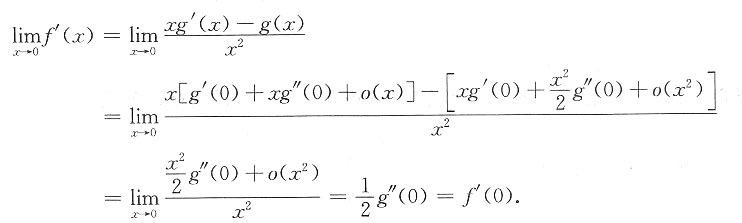
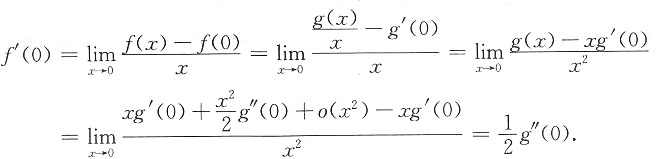
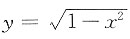 所围成的平面图形的形心坐标为______
所围成的平面图形的形心坐标为______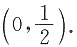
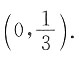
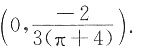
 .把平面图形分成D1,D2两部分
.把平面图形分成D1,D2两部分
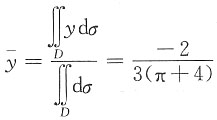 ,所以形心坐标为
,所以形心坐标为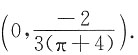
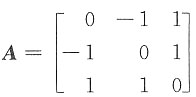 ,则当kE+A是正定矩阵时,k应满足条件______
,则当kE+A是正定矩阵时,k应满足条件______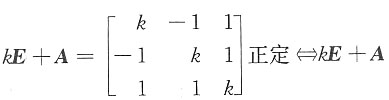 的全部顺序主子式大于零.
的全部顺序主子式大于零.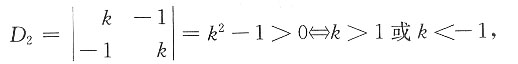
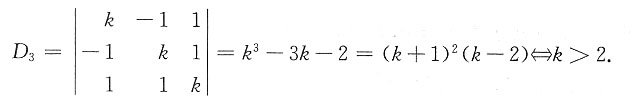
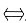 k>2.
k>2.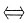 kE+A的特征值全部大于零,A的特征多项式为
kE+A的特征值全部大于零,A的特征多项式为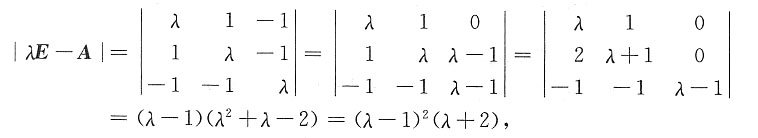
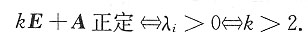
 则|A|中第k行元素代数余子式之和Ak1+Ak2+…Akn=______
则|A|中第k行元素代数余子式之和Ak1+Ak2+…Akn=______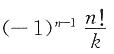




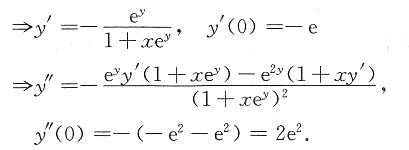
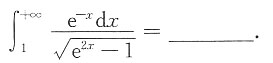
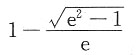
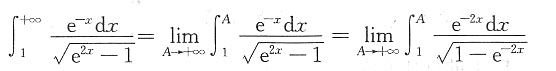
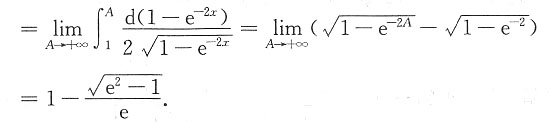
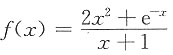 的斜渐近线为______.
的斜渐近线为______.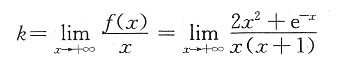
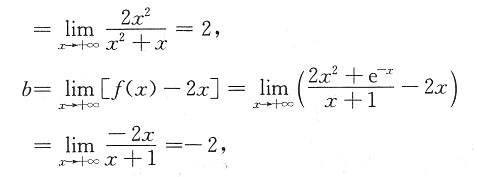
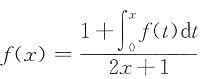 ,则f(x)=______.
,则f(x)=______.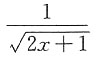
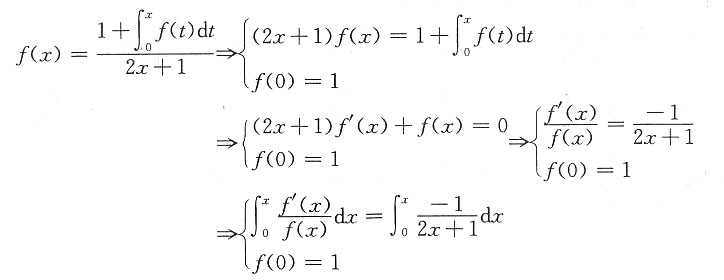
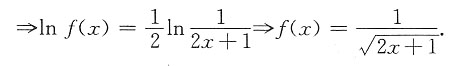
 λ(λ-3)(λ+7)=0.
λ(λ-3)(λ+7)=0.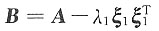 的全部特征值是______.
的全部特征值是______.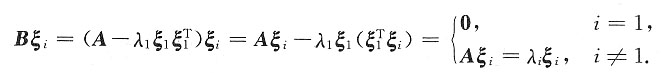
 的特征值为0,λ2,λ3,…,λn.
的特征值为0,λ2,λ3,…,λn.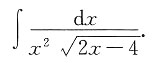
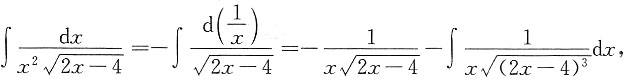
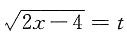 ,则
,则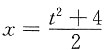 ,dx=tdt,于是
,dx=tdt,于是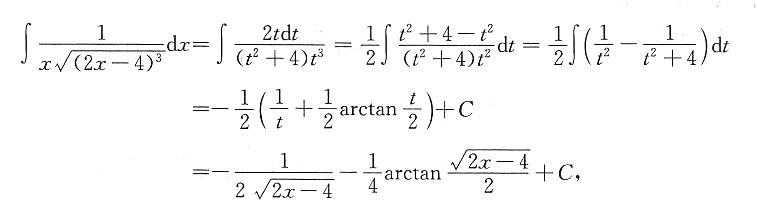
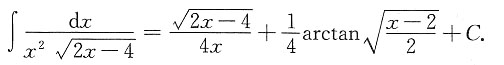
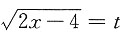 ,则
,则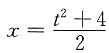 ,dx=tdt,于是
,dx=tdt,于是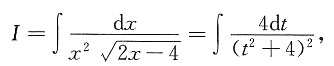
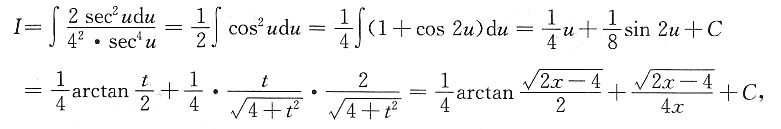

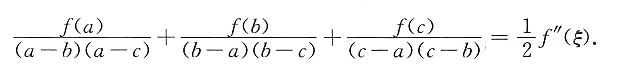
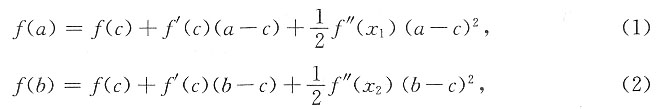
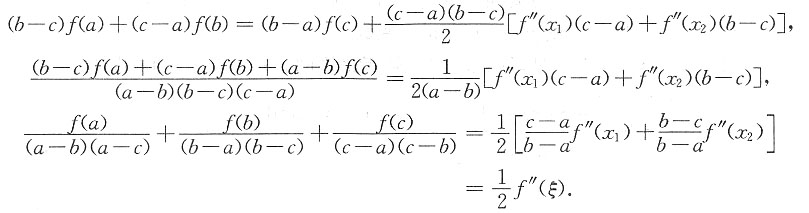
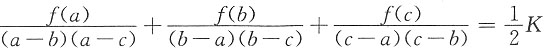 ,则
,则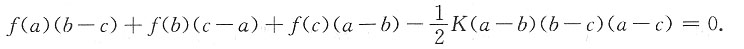
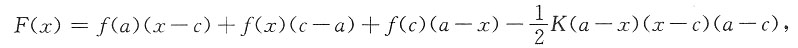
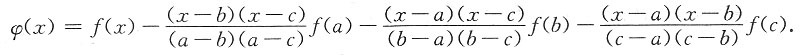
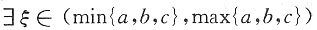 ,使
,使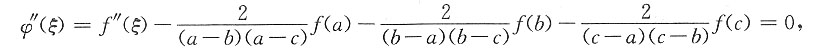
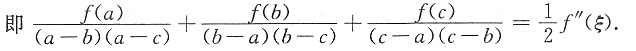
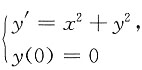 的唯一解.
的唯一解.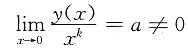 ,求常数k和a的值;
,求常数k和a的值;
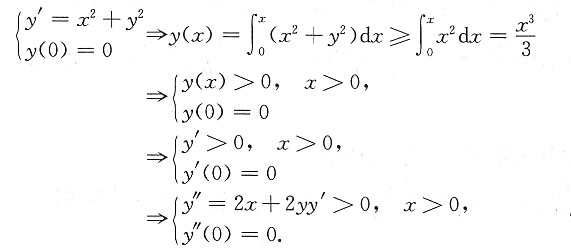
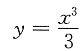 之上,函数图形如下图所示.
之上,函数图形如下图所示.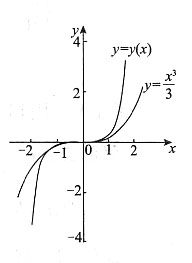
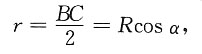
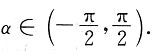
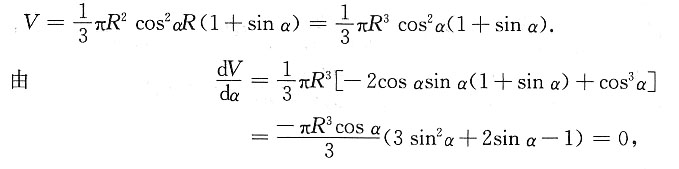
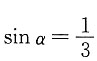 .故当内接正圆锥的底面直径为
.故当内接正圆锥的底面直径为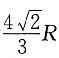 、高为
、高为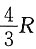 时,其体积最大,最大体积为
时,其体积最大,最大体积为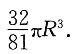
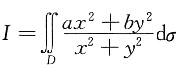 的值.
的值.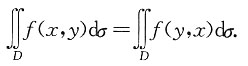
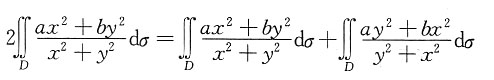
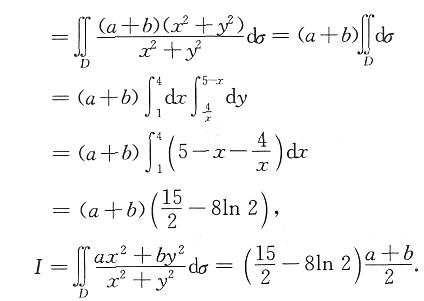

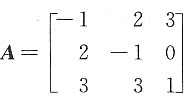 ,有特征向量ξ=[1,-2,1]T,求A的对应于特征向量ξ的特征值λ.AT有特征值μ=4,求AT对应特征值μ=4的特征向量.
,有特征向量ξ=[1,-2,1]T,求A的对应于特征向量ξ的特征值λ.AT有特征值μ=4,求AT对应特征值μ=4的特征向量.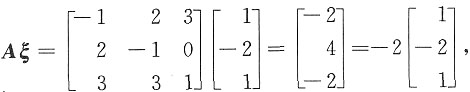 故A对应于ξ的特征值为λ=-2.
故A对应于ξ的特征值为λ=-2.