银符考试题库B12
现在是:
试卷总分:100.0
您的得分:
考试时间为:
点击“开始答卷”进行答题
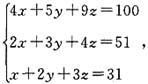 解得
解得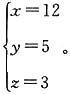 所以如果安排大、中、小卡车各1辆运送这批货物,全部运完需要
所以如果安排大、中、小卡车各1辆运送这批货物,全部运完需要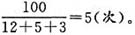 故本题答案为B。
故本题答案为B。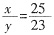 。目前该产品的成本利润率为
。目前该产品的成本利润率为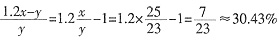 。
。 。加工后,圆木的底面即为原方木的内切圆,底面半径为
。加工后,圆木的底面即为原方木的内切圆,底面半径为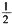 ,底面积为
,底面积为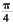 。加工后的方木底面为圆木的内接正方形,其对角线为
。加工后的方木底面为圆木的内接正方形,其对角线为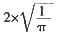 ,面积为
,面积为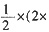
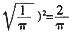 。故二者体积比为底而积之比,为π2:8。
。故二者体积比为底而积之比,为π2:8。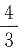 倍,则8年后小明的年龄是______岁。
倍,则8年后小明的年龄是______岁。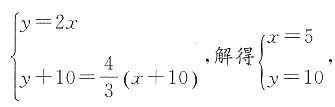 则8年后小明年龄为5+8=13(岁)。故选C。
则8年后小明年龄为5+8=13(岁)。故选C。 小时后相遇,则此时甲比乙多走
小时后相遇,则此时甲比乙多走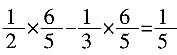 ,所以A、B相距
,所以A、B相距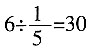 千米。
千米。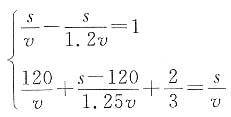
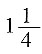 圈和
圈和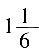 圈,若甲、乙、丙同时从起点出发,则甲滑多少圈后三人再次在起点相遇?
圈,若甲、乙、丙同时从起点出发,则甲滑多少圈后三人再次在起点相遇?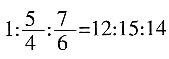 ,因此甲滑12圈的时候,乙和丙分别滑了15、14圈,三人正好在起点相遇。另解,要使三人再次在起点相遇,则甲滑的圈数应为4和6的最小公倍数,即12圈。
,因此甲滑12圈的时候,乙和丙分别滑了15、14圈,三人正好在起点相遇。另解,要使三人再次在起点相遇,则甲滑的圈数应为4和6的最小公倍数,即12圈。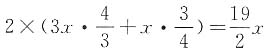 ,故需要的时间为
,故需要的时间为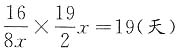 。
。 。因此,这样的不同的等差数列有180个。本题正确答案为B。
。因此,这样的不同的等差数列有180个。本题正确答案为B。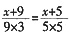 ,解得x=45,则开始检票时已到达45个观众,即第一个观众已到达45分钟,到达时间为7:45。
,解得x=45,则开始检票时已到达45个观众,即第一个观众已到达45分钟,到达时间为7:45。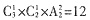 种;然后把两名异性歌手和少年歌手捆绑后与剩余的3个人一起排列,方法数有
种;然后把两名异性歌手和少年歌手捆绑后与剩余的3个人一起排列,方法数有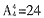 种,因此总方法数是12×24=288种。
种,因此总方法数是12×24=288种。
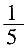 ,结果比原计划推迟20分钟完成任务,这批零件有多少个?
,结果比原计划推迟20分钟完成任务,这批零件有多少个?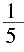 ,同样的数量时间上要多花费
,同样的数量时间上要多花费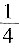 。则160个零件原来计划花费
。则160个零件原来计划花费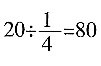 分钟。原计划2小时加工完,80分钟占
分钟。原计划2小时加工完,80分钟占 。那么总的零件数是
。那么总的零件数是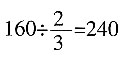 个。
个。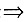 每人都擦5块,可多擦2块,则余12-2=10块。问题转化为:每人擦5块,余10块;每人擦6块,正好。
每人都擦5块,可多擦2块,则余12-2=10块。问题转化为:每人擦5块,余10块;每人擦6块,正好。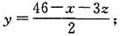 当x=z=0时,y值最大,最大值为23。
当x=z=0时,y值最大,最大值为23。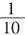 ,乙的工作效率比单独做时提高
,乙的工作效率比单独做时提高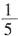 ,甲、乙合作6小时完成了这项工作。如果甲单独做需要11小时,那么乙单独做需要几小时?______
,甲、乙合作6小时完成了这项工作。如果甲单独做需要11小时,那么乙单独做需要几小时?______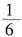 ,甲单独做的效率是
,甲单独做的效率是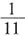 。合作时效率提高
。合作时效率提高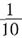 ,因此甲合作时候的效率是
,因此甲合作时候的效率是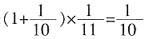 。那么乙合作时候的效率就是
。那么乙合作时候的效率就是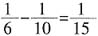 。乙单独做的时候是合作时候的
。乙单独做的时候是合作时候的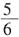 ,因此乙单独做效率是
,因此乙单独做效率是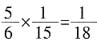 ,即要做18小时。
,即要做18小时。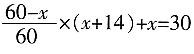 ,解得x=10(x=96舍去)。
,解得x=10(x=96舍去)。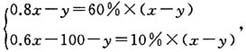 解得
解得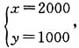 所以该液晶电视按原价销售时所得利润为2000-1000=1000(元)。故本题答案为C。
所以该液晶电视按原价销售时所得利润为2000-1000=1000(元)。故本题答案为C。