银符考试题库B12
现在是:
试卷总分:100.0
您的得分:
考试时间为:
点击“开始答卷”进行答题

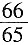
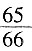
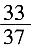
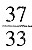
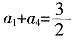 ,即
,即 ,下面3节的长度共4尺,则a8=a1+7d=
,下面3节的长度共4尺,则a8=a1+7d=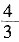 ,可求得
,可求得 ,第6节的长度为
,第6节的长度为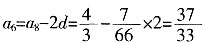 ,选择D。
,选择D。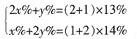
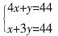 解得y=12,选择D选项。
解得y=12,选择D选项。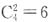 (种)选择,故总人数至少为6×4+1=25(名)。
(种)选择,故总人数至少为6×4+1=25(名)。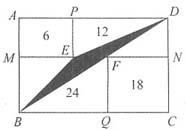
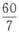
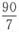
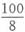
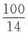
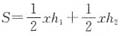 。
。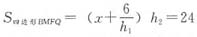 , ①
, ① 。 ②
。 ②
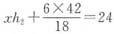 ,得xh2=10,
,得xh2=10,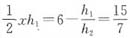 。
。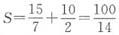 。
。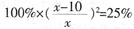 ,解得x=20,选A。
,解得x=20,选A。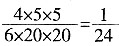 ,在4%到5%之间,选择B。
,在4%到5%之间,选择B。| 甲 | 乙 | 丙 | 总计 | ||||||||||||||||||||||||||||
| 人数比 | 10:8:7=20:16:14 | ||||||||||||||||||||||||||||||
| 男女比例 | 3:1 | 5:3 | 5:9 | 3:2 | |||||||||||||||||||||||||||
| 男 | 15 | 10 | 30-15-10=5 | 30 | |||||||||||||||||||||||||||
| 女 | 5 | 6 | 20-11=9 | 20 | |||||||||||||||||||||||||||
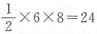 。
。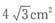 ,则阴影部分的面积是______cm2。
,则阴影部分的面积是______cm2。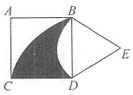
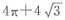
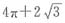
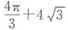
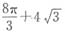
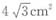 ,可得
,可得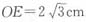 。阴影部分的面积=扇形BCD的面积+△BED的面积-扇形BDE的面积。扇形BCD面积=R2×π×n÷360=16×π×90÷360=4π(cm2),△BED面积=
。阴影部分的面积=扇形BCD的面积+△BED的面积-扇形BDE的面积。扇形BCD面积=R2×π×n÷360=16×π×90÷360=4π(cm2),△BED面积= cm2。因为OD=2cm,
cm2。因为OD=2cm, ,又因为BE=DE,BD=4cm,故BE=DE=BD=4cm,所以△BED为等边三角形,故∠BED=60°。扇形BDE的面积=
,又因为BE=DE,BD=4cm,故BE=DE=BD=4cm,所以△BED为等边三角形,故∠BED=60°。扇形BDE的面积=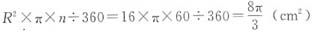 ,综上所述,可得阴影部分的面积为
,综上所述,可得阴影部分的面积为 。
。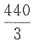
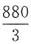
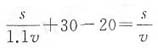 ,得出
,得出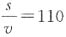 ,他们下山需要的时间为
,他们下山需要的时间为 (分钟)。故答案为A。
(分钟)。故答案为A。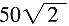
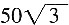

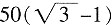
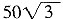 。
。
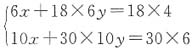 ,解得x=3,
,解得x=3,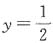 。再设放z头牛吃8亩草,24天可以吃完,得
。再设放z头牛吃8亩草,24天可以吃完,得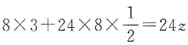 ,解得z=5。
,解得z=5。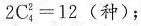 也可以是一批1人另外一批3人,分批后排列有
也可以是一批1人另外一批3人,分批后排列有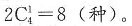 3批撞线有
3批撞线有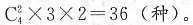 4批撞线有4×3×2×1=24(种)。综上,共有1+12+8+36+24=81(种),选D。
4批撞线有4×3×2×1=24(种)。综上,共有1+12+8+36+24=81(种),选D。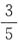 ,小钱用自己钱数的
,小钱用自己钱数的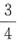 ,小孙用自己钱数的
,小孙用自己钱数的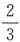 ,小李用自己钱数的
,小李用自己钱数的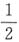 ,各买了一本相同的书。则剩余钱最多的人比最少的人多______元钱。
,各买了一本相同的书。则剩余钱最多的人比最少的人多______元钱。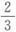 后,以定价的8折将余下的衬衫全部售出,该网店的预计盈利为成本的______。
后,以定价的8折将余下的衬衫全部售出,该网店的预计盈利为成本的______。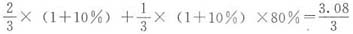 。盈利为成本的
。盈利为成本的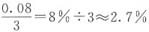 。
。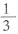 ,C管注水速度增加1.5倍,三个管总注水速度不变。则B池注满80%时,C池还差多少注满?
,C管注水速度增加1.5倍,三个管总注水速度不变。则B池注满80%时,C池还差多少注满?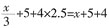 ,解得x=9。B池由50010到80%用时30%÷5=6%,这段时间C池注了6%×10=60%,之前注了40%刚好注满。因此,C池还差0%注满。
,解得x=9。B池由50010到80%用时30%÷5=6%,这段时间C池注了6%×10=60%,之前注了40%刚好注满。因此,C池还差0%注满。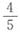
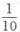
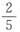
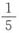
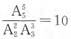 (种)不同的排列。即这五张卡片能排成10种不同的单词。所以恰好排成BABAB或BBBAA的概率为
(种)不同的排列。即这五张卡片能排成10种不同的单词。所以恰好排成BABAB或BBBAA的概率为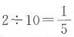 。
。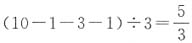 (条),此时份数不为整数,故假设不成立,排除A项。(2)假设三人共钓到15条鱼,则小雨先将鱼分为3份,每份
(条),此时份数不为整数,故假设不成立,排除A项。(2)假设三人共钓到15条鱼,则小雨先将鱼分为3份,每份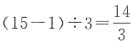 (条),此时份数不为整数,故假设不成立,排除B项。(3)假设三人共钓到20条鱼,则小雨先将鱼分为3份,每份
(条),此时份数不为整数,故假设不成立,排除B项。(3)假设三人共钓到20条鱼,则小雨先将鱼分为3份,每份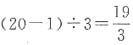 (条),此时份数不为整数,故假设不成立,排除C项。(4)假设三人共钓到25条鱼,则小雨先将鱼分为3份,每份(25-1)÷3=8(条),小蕾再将鱼分为3份,每份为(25-1-8-1)÷3=15÷3=5(条),小溪再将鱼分为3份,每份(15-1-5)÷3=3(条),此时份数仍为整数,故假设成立。故本题答案为D项。
(条),此时份数不为整数,故假设不成立,排除C项。(4)假设三人共钓到25条鱼,则小雨先将鱼分为3份,每份(25-1)÷3=8(条),小蕾再将鱼分为3份,每份为(25-1-8-1)÷3=15÷3=5(条),小溪再将鱼分为3份,每份(15-1-5)÷3=3(条),此时份数仍为整数,故假设成立。故本题答案为D项。