银符考试题库B12
现在是:
试卷总分:100.0
您的得分:
考试时间为:
点击“开始答卷”进行答题
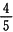 ,乙组的工作效率只有原来的
,乙组的工作效率只有原来的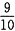 。现在计划16天做完这批衣服,且要求两组合作的天数尽可能少,那么两组要合作几天?______
。现在计划16天做完这批衣服,且要求两组合作的天数尽可能少,那么两组要合作几天?______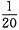 ,乙工作组的工作效率为
,乙工作组的工作效率为 ,两组合作的效率为
,两组合作的效率为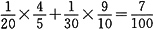 ,两组合作效率>甲组效率>乙组效率。若要16天完成,且甲乙合作的天数尽可能少,那么就应让效率较高的甲组多做,16天内实在来不及的则由甲乙合作完成。设合作天数为x,则甲组独做(16-x)天,得
,两组合作效率>甲组效率>乙组效率。若要16天完成,且甲乙合作的天数尽可能少,那么就应让效率较高的甲组多做,16天内实在来不及的则由甲乙合作完成。设合作天数为x,则甲组独做(16-x)天,得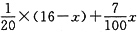 =1,解得x=10。本题正确答案为B。
=1,解得x=10。本题正确答案为B。| 序号 | 操作过程 |
| 1 | 将7千克桶倒满 |
| 2 | 将7千克桶中的水倒满5千克桶,此时7千克桶中有2千克水 |
| 3 | 将5千克桶中的水倒掉 |
| 4 | 将7千克桶中的2千克水倒入5千克桶 |
| 5 | 将7千克桶倒满 |
| 6 | 将7千克桶中的水倒满5千克桶,此时7千克桶中有4千克水 |
| 7 | 将5千克桶中的水倒掉 |
| 8 | 将7千克桶中的4千克水倒入5千克桶 |
| 9 | 将7千克桶倒满 |
| 10 | 将7千克桶中的水倒满5千克桶,此时7千克桶中有6千克水 |

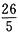
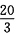
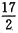
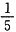 ,乙丙两队的效率之和为
,乙丙两队的效率之和为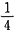 。乙队先做6小时后离开,甲丙两队接着合作2小时正好做完,可以转化为甲乙合作2小时,乙丙合作2小时,乙再单独2小时正好做完。则乙单独2小时完成的工作量为
。乙队先做6小时后离开,甲丙两队接着合作2小时正好做完,可以转化为甲乙合作2小时,乙丙合作2小时,乙再单独2小时正好做完。则乙单独2小时完成的工作量为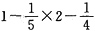 ×2=
×2=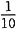 。所以乙的效率为
。所以乙的效率为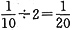 。则甲的效率为
。则甲的效率为 ,甲单独完成这项工程所需的时间为
,甲单独完成这项工程所需的时间为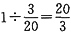 (小时)。
(小时)。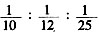 ,即30:25:12。工作完成时甲比丙多加工
,即30:25:12。工作完成时甲比丙多加工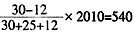 个零件。
个零件。
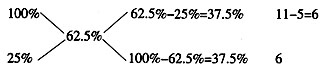
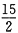
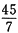
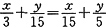 ,解得y=2x。则甲的平均速度为(x+y)÷(
,解得y=2x。则甲的平均速度为(x+y)÷(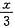 +
+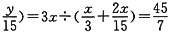 (千米/时)。故正确答案为C。
(千米/时)。故正确答案为C。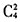 种方法,再把3组学生分配到3所学校有
种方法,再把3组学生分配到3所学校有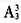 种方法,故所求为
种方法,故所求为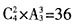 种。
种。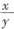 ,甲走0B的距离用时为
,甲走0B的距离用时为 ,所以
,所以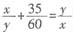 。把
。把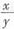 用m替换,12m2+7m-12=0,解得
用m替换,12m2+7m-12=0,解得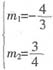 ,m不可能为负数,所以选D。
,m不可能为负数,所以选D。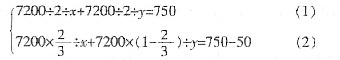
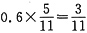 。又因为新兴小学、红梅小学两学校获奖的人数比为6:5,所以设总人数为11份,新兴小学得奖的人数占其中6份。可知新兴小学获新人奖者占该校获奖总人数的比重为
。又因为新兴小学、红梅小学两学校获奖的人数比为6:5,所以设总人数为11份,新兴小学得奖的人数占其中6份。可知新兴小学获新人奖者占该校获奖总人数的比重为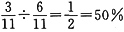 。
。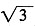 cm,则此球的体积为:
cm,则此球的体积为: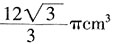
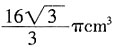
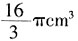
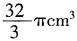
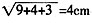 ,则外接球的半径为2cm。球的体积为
,则外接球的半径为2cm。球的体积为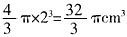 。
。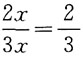 。故B项当选。
。故B项当选。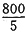 =160个。
=160个。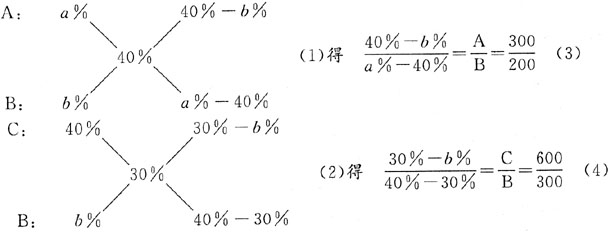
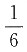
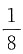

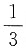
 (种)拿法。若恰好有两名同学拿到自己写的明信片,则另外三人中不能有人拿到自己写的明信片。据此,另外三人拿明信片的方法种数=2×1×1=2(种),故恰好有两名同学拿到自己写的明信片的拿法种数=
(种)拿法。若恰好有两名同学拿到自己写的明信片,则另外三人中不能有人拿到自己写的明信片。据此,另外三人拿明信片的方法种数=2×1×1=2(种),故恰好有两名同学拿到自己写的明信片的拿法种数= (种)。因此恰有两名同学拿到自己写的明信片的概率为
(种)。因此恰有两名同学拿到自己写的明信片的概率为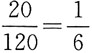 。
。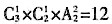 种;然后把两名异性歌手和少年歌手捆绑后与剩余的3个人一起排列,方法数有
种;然后把两名异性歌手和少年歌手捆绑后与剩余的3个人一起排列,方法数有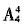 =24种,因此总方法数是12×24=288种。
=24种,因此总方法数是12×24=288种。