第Ⅰ卷(选择题)
一、选择题(在每小题给出的四个选项中,只有一项是符合题目要求的)1. 若
,则a=______
A.
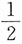
B.1
C.
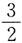
D.2
A B C D
D
[考点] 本题考查了特殊极限
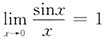
的应用的知识点.
[解析]
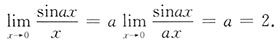
3. 下列极限计算正确的是______
A.
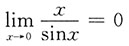
B.
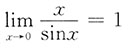
C.
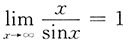
D.
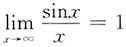
A B C D
B
[考点] 本题考查了极限的知识点.
[解析] 对于选项A:
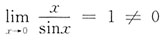
,错误;对于选项B:
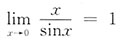
,正确;对于选项C:
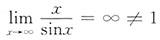
,错误;时于选项D:
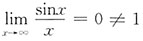
,错误.
4. 设f'(1)=1,则

等于______
A.0
B.1
C.
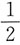
D.2
A B C D
C
[考点] 本题考查了利用导数定义求极限的知识点.
[解析] 因f'(1)=1,于是
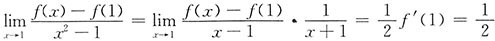
.
5. 下列极限等于1的是______
A.
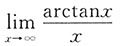
B.
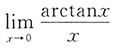
C.
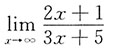
D.
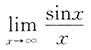
A B C D
B
[考点] 本题考查了极限的知识点.
[解析]
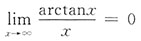
(arctanx是有界函数),
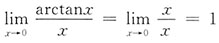
(用无穷小代换:arctanx~x(x→0)),
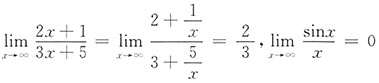
(x→∞时
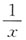
为无穷小量,而sinx是有界函数,注意
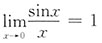
).
6. 下列反常积分收敛的是______
A.
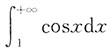
B.
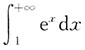
C.
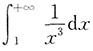
D.
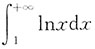
A B C D
C
[考点] 本题考查了无穷区间的反常积分的敛散性的知识点.
[解析] 对于选项A:
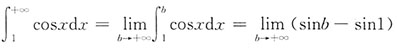
不存在,此积分发散;对于选项B:
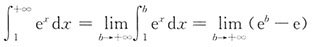
不存在,此积分发散;对于选项C:
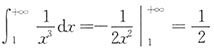
,此积分收敛;对于选项D:
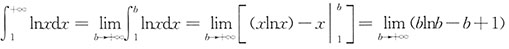
不存在,此积分发散.
8. 函数y=|x|+1在x=0处______
A B C D
C
[考点] 本题考查了函数在一点可导、连续的性质的知识点.
[解析] 从四个选项的内容来看,我们可以一步一步地处理,x=0时,y=1,
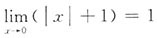
,故f(x)在x=0处连续.y在x=0的可导性可从左右导数出发进行讨论.
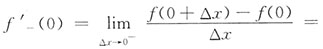

,由于f'
+(0)≠f'
-(0),所以f(x)在x=0处不可导,故应选C.
9.
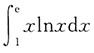
=______
A.0
B.
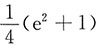
C.
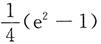
D.e
2-1
A B C D
B
[考点] 本题考查了分部积分法的知识点.
[解析]
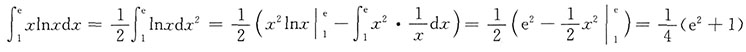
.
10. 设z=(3x
2+y
2)
xy,则

等于______
- A.xy·(3x2+y2)xy-1
- B.(3x2+y2)xy·ln(3x2+y2)
- C.y·(3x2+y2)xy[(3x2+y2)ln(3x2+y2)+6x2]
- D.y·(3x2+y2)xy-1[(3x2+y2)ln(3x2+y2)+6x2]
A B C D
D
[考点] 本题考查了二元函数的一阶偏导数的知识点.
[解析] 因z=(3x
2+y
2)
xy可看作是z=u
v,u=3x
2+y
2,v=xy复合而成,
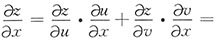
v·u
v-1·6x+u
v·lnu·y=xy·(3x
2+y
2)
xy-1·6x+(3x
2+y
2)
xy·ln(3x
2+y
2)·y=y·(3x
2+y
2)
xy-1·[(3x
2-y
2)ln(3x
2+y
2)+6x
2].
三、解答题(解答应写出推理、演算步骤)1.
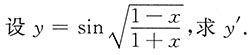
2. 一批零件中有10个合格品,3个次品,安装机器时,从这批零件中任取一个,取到合格品才能安装.若取出的是次品,则不再放回,求在取得合格品前已取出的次品数X的概率分布.
由题意,X的可能取值为0,1,2,3.X=0,即第一次就取到合格品,没有取到次品,

;X=1,即第一次取到次品,第二次取到合格品,
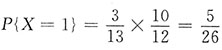
;同理,
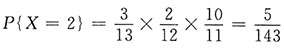
;
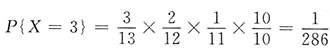
.
所以X的概率分布为

3.
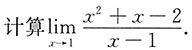
4. 试用夹逼定理证明:
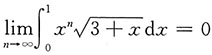
.
5. 设函数z=x
3y+xy
3,求
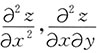
.
6.
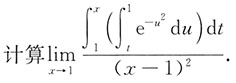
由洛必达法则

注:要使用洛必达法则必须检验定理的条件是否满足,由于

.因此可使用洛必达法则.
7. 设x
1=1,x
2=2均为y=alnx+bx
2+3x的极值点,求a,b.
由y=alnx+bx
2+3x,则
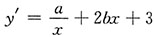
.
因为x
1=1,x
2=2是极值点,所以y'|
x=1=0,y'|
x=2=0,即
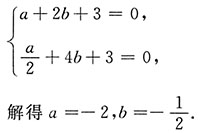
8.