第Ⅰ卷(选择题)
一、选择题(在每小题给出的四个选项中,只有一项是符合题目要求的)1. 设函数
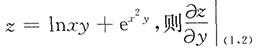
=______
A.
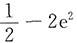
B.
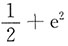
C.1+2e
2 D.1+e
2 A B C D
B
[考点] 本题考查了二元函数的一点处的一阶偏导数的知识点.
[解析]
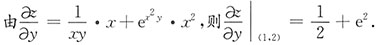
也可先将x=1代入,则z|
(1,y)=lny+e
y,
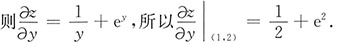
7. 下列变量在给定的变化过程中是无穷小量的是______
A.
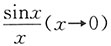
B.2
-x-2(x→0)
C.
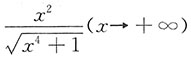
D.
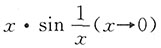
A B C D
D
[考点] 本题考查了无穷小量的知识点.
[解析] 由
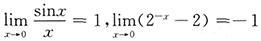
,故由无穷小量知应选D.
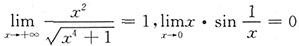
.
9. 甲、乙两人独立地对同一目标射击一次,其命中率分别为0.6和0.5,现已知目标被命中,是甲射中的概率为______
A B C D
B
[考点] 本题考查了条件概率的知识点.
[解析] 设A
1={甲射中目标},A
2={乙射中目标},B={目标被命中}.由题意,P(A
1)=0.6,P(A
2)=0.5,B=A
1∪A
2,
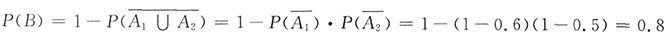
;故所求概率为
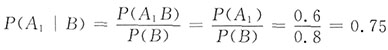
.
三、解答题(解答应写出推理、演算步骤)1.
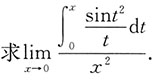
2.
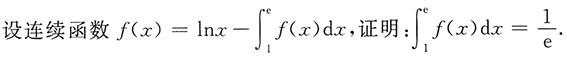
3. 求曲线y=x
2与该曲线在x=a(a>0)处的切线与x轴所围的平面图形的面积.
如图所示,在x=a处切线的斜率为y'|
x=a=2a,切线方程为y-a
2=2a(x-a),
即y=2ax-a
2,
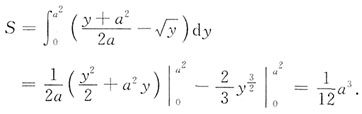
4. 设f(x)是连续函数,且
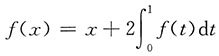
,求f(x).
5. 试确定a,b的值,使函数
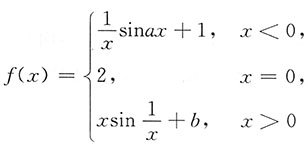
在点x=0处连续.
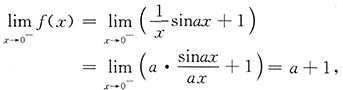
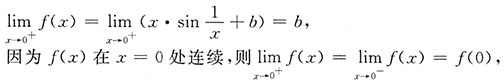
即a+1=b=2,即a=1,b=2.
6. 从一批有10件正品及2件次品的产品中,不放回地一件一件地抽取产品.设每个产品被抽到的可能性相同.求直到取出正品为止所需抽取的次数X的概率分布.
由题意,X的所有可能的取值为1,2,3,
X=1,即第一次就取到正品,
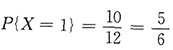
;
X=2,第一次取到次品且第二次取到正品,

;
同理,
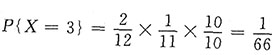
,
故X的概率分布如下
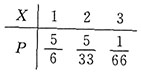
7.
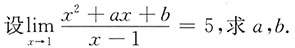
8. 求y=f(x)=2x
3-3x
2-12x+14的极值点和极值,以及函数曲线的凸凹性区间和拐点.
y'=6x
2-6x-12,y"=12x-6,
令y'=0得驻点x
1=-1,x
2=2,
当x
2=2时,y"=18>0.所以f(x)在x=2处取极小值-6.
当x
1=-1时,y"<0.所以f(x)在x=-1处取极大值21.
又令y"=0,得
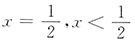
时,y"<0,从而曲线为凸的,即函数曲线的凸区间为
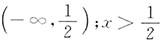
时,y">0,从而曲线为凹的,即函数曲线的凹区间为
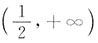
;又因
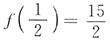
,故曲线的拐点为

.