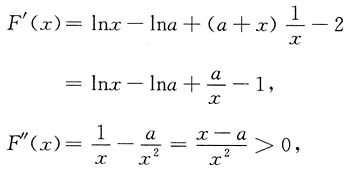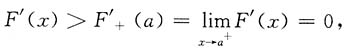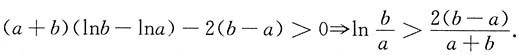一、选择题下列每题给出的四个选项中,只有一个选项是符合题目要求的.1. 设正项级数
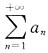
收敛,则
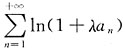
(λ>0为常数)______
- A.收敛.
- B.发散.
- C.收敛性不确定.
- D.敛散性与λ有关.
A B C D
A
[解析] 由等价无穷小,得ln(1+λa
n)~λa
n,而

收敛,故
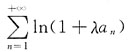
收敛.选A.
4. 由曲线
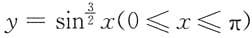
与x轴围成的图形绕x轴旋转所成旋转体的体积为______
A.
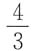
B.
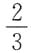
C.
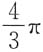
D.
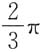
A B C D
C
[解析]
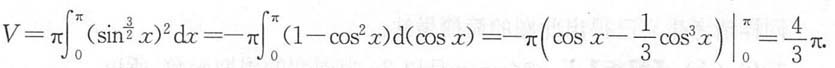
5. 已知
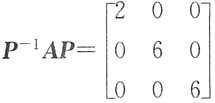
,α
1是矩阵A属于特征值λ=2的特征向量,α
2,α
3是矩阵A属于特征值λ=6的线性无关的特征向量,那么矩阵P不能是______
- A.[α1,-α2,α3]
- B.[α1,α2+α3,α2-2α3]
- C.[α1,α3,α2]
- D.[α1+α2,α1-α2,α3]
A B C D
D
[解析] 若
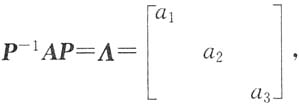
P=[α
1,α
2,α
3],则有AP=PΛ.即
即[Aα
1,Aα
2,Aα
3]=[a
1α
1,a
2α
2,a
3α
3].
可见α
i是矩阵A属于特征值a
1的特征向量(i=1,2,3),又因矩阵P可逆,因此,α
1,α
2,α
3线性无关.
若α是属于特征值λ的特征向量,则-α仍是属于特征值λ的特征向量,故(A)正确.
若α,β是属于特征值λ的特征向量,则k
1α+k
2β仍是属于特征值λ的特征向量.本题中,α
2,α
3是属于λ=6的线性无关的特征向量,故α
2+α
3,α
2-2α
3仍是λ=6的特征向量,并且α
2+α
3,α
2-2α
3线性无关,故(B)正确.
关于(C),因为α
2,α
3均是λ=6的特征向量,所以α
2,α
3谁在前谁在后均正确,即(C)正确.
由于α
1,α
2是不同特征值的特征向量,因此α
1+α
2,α
1-α
2不再是矩阵A的特征向量,故(D)错误.
6. 设f(x,y)连续,且
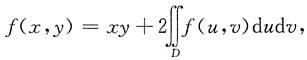
其中D:x
2+y
2=2x,则f(x,y)=______
- A.xy.
- B.xy+1.
- C.xy+2.
- D.2xy.
A B C D
A
[解析] 令
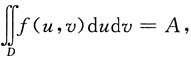
则f(x,y)=xy+2A,两边对x,y在D上积分,得
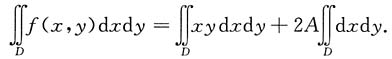
因为D:x
2+y
2=2x关于x轴对称,被积函数xy关于y为奇函数,所以
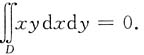
于是A=2Aπ,即A=0,故f(x,y)=xy.
7. 设α
1,α
2,…,α
s和β
1,β
2,…,β
t为两个n维向量组,且r(α
1,α
2,…,α
s)=r(β
1,β
2,…,β
t)=r,则______
- A.两向量组等价
- B.r(α1,α2,…,αs,β1,β2,…,βt)=r
- C.当α1,α2,…,αs可被β1,β2,…,βt线性表出时,β1,β2,…,βt也可被(α1,α2,…,αs线性表出
- D.当s=t时两向量组等价
A B C D
C
[解析] 不妨设α1,α2,…,αs的极大无关组为α1,α2,…,αr;β1,β2,…,βt的极大无关组为β1,β2,…,βr,则考虑:
α1,…,αs;β1,…,βt(*)
若α1,…,αs可被β1,…,βt线性表示,则α1,…,αr也可被β1,…,βr表示,即β1,…,βt是(*)式的极大无关组,又α1,…,αr线性无关,故α1,…,αr也是(*)的极大无关组,从而β1,…,βt可由α1,…,αr线性表示,故β1,β2,…,βt也可由α1,α2,…,αs线性表示,因此C成立.
9. 设齐次线性方程组Ax=0有解α
1=(1,2,1,3)
T,α
2=(1,1,-1,1)
T,α
3=(1,3,3,5)
T,α
4=(4,5,-2,6)
T.其余Ax=0的解向量均可由α
1,α
2,α
3,α
4线性表出,则Ax=0的基础解系为______
- A.α1,α2.
- B.α1,α2,α3.
- C.α2,α3,α4.
- D.α1,α2,α3,α4.
A B C D
A
[解析] 向量组α
1,α
2,α
3,α
4的极大线性无关组为Ax=0的基础解系,因为

显然,α
1,α
2是α
1,α
2,α
3,α
4的极大无关组.故选A.
二、填空题1. 方程组
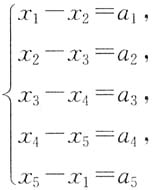
有解的充要条件是______.
[解析]
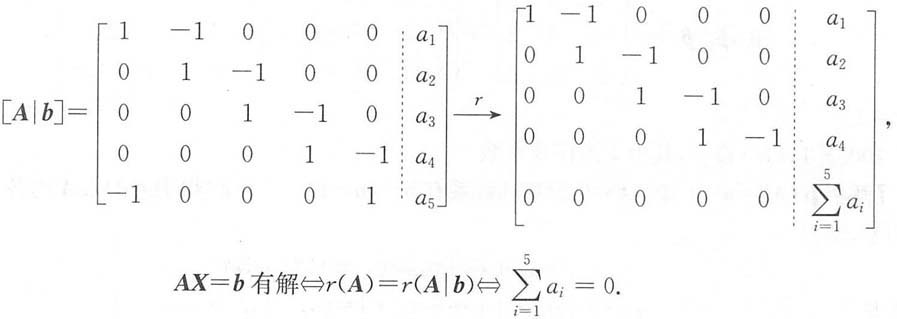
2. 设f(x)连续,f(0)=1,则曲线
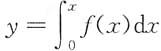
在(0,0)处的切线方程是______.
y=x
[解析] 曲线在(0,0)处切线斜率
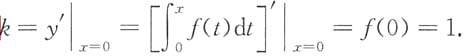
所以曲线在(0,0)处,切线方程为y=x.
3. 设二维随机变量(X,Y)服从二维正态分布,且X~N(0,3),Y~N(0,4),相关系数ρ
XY=
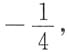
则(X,Y)的概率密度f(x,y)为______.
[解析]
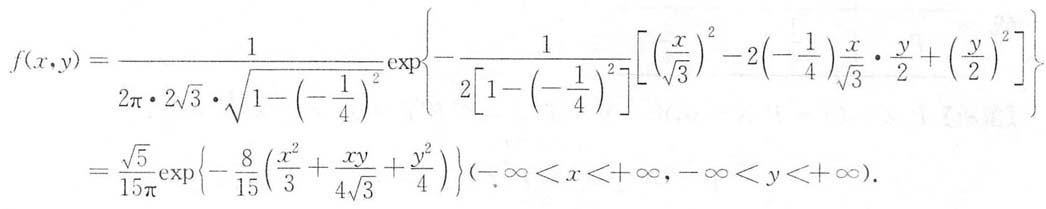
4. 设A为三阶实对称矩阵,α
1=(a,-a,1)
T是方程组AX=0的解,α
2=(a,1,1-a)
T是方程组(A+E)X=0的解,则a=______.
1
[解析] 因为A为实对称矩阵,所以不同特征值对应的特征向量正交,因为AX=0及(A+E)X=0有非零解,所以λ
1=0,λ
2=-1为矩阵A的特征值,α
1=(a,-a,1)
T,α
2=(a,1,1-a)
T是它们对应的特征向量,所以有
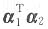
=a
2-a+1-a=0,解得a=1.
5. 若当x→0时,有
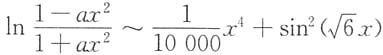
,则a=______.
-3
[解析] 当x→0时,
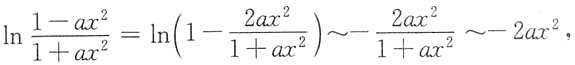
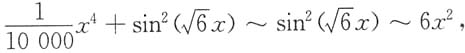
故a=-3.
6. 设总体X服从参数为2的指数分布,从总体X中抽取简单随机样本X
1,X
2,X
3,
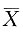
是样本均值,则
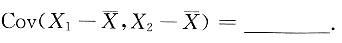
[解析] 由于X
1,X
2,X
3为来自总体X~E(2)的简单随机样本,所以
Cov(X
i,X
j)=0,i≠j(i,j=1,2,3),
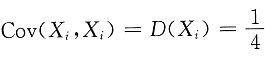
,i=1,2,3.
从而
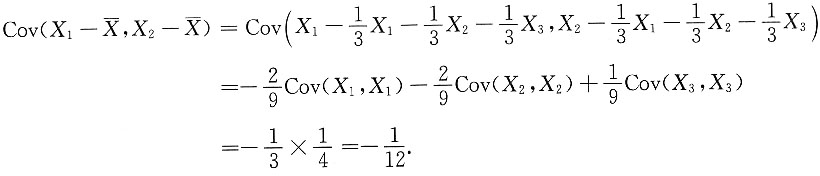
三、解答题共70分.解答应写出文字说明、证明过程或演算步骤.1. 计算
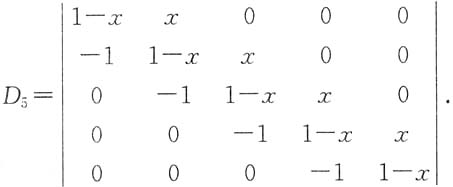
解:按第一行展开
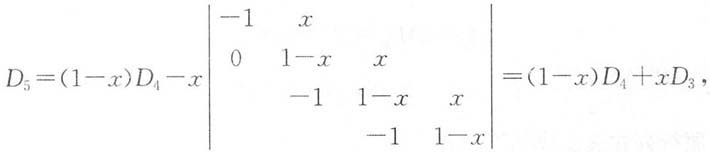
得到递推公式
D
5-D
4=-x(D
4-D
3)=…=-x
3(D
2-D
1).
由于
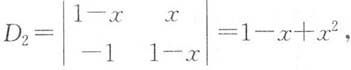
D
1=1-x,于是得
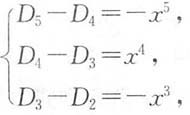
容易推出D
5=-x
5+x
4-x
3+D
2=-x
5+x
4-x
3+x
2-x+1.
2. 设f(x
1,x
2,x
3)=X
TAX,r(A)=1,A的每行元素之和为2,当X=β=[2,4,0]
T时,
求f(x
1,x
2,x
3)=X
TAX在β处的值,即f(x
1,x
2,x
3)|
X=β=β
TAβ.
解:因
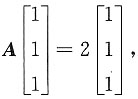
A有λ
1=2,对应的特征向量为
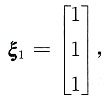
又r(A)=1,|A|=0,故A有特征值λ
2=λ
3=0(二重),对应λ
2=λ
3=0的特征向量设为ξ=[x
1,x
2,x
3]
T,则ξ和ξ
1正交.
易得ξ
2=[1,-1,0]
T,ξ
3=[1,1,-2]
T(取ξ
2也与ξ
3正交),将β由ξ
1,ξ
2,ξ
3线性表示,设为β=x
1ξ
1+x
2ξ
2+x
3ξ
3,由
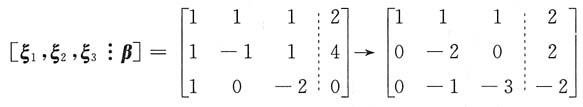
解得x
1=2,x
2=-1,x
3=1,即β=2ξ
1-ξ
2+ξ
3.故
f(x
1,x
2,x
3)|
X=β=β
TAβ=(2ξ
1-ξ
2+ξ
3)
TA(2ξ
1-ξ
2+ξ
3)
=(2ξ
1-ξ
2+ξ
3)
TA·2ξ
1=4(2ξ
1-ξ
2+ξ
3)
Tξ
1 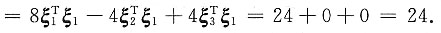
也可由A[ξ
1,ξ
2,ξ
3]=[2ξ
1,ξ
2,ξ
3]直接求得A,再计算β
TAβ.其中
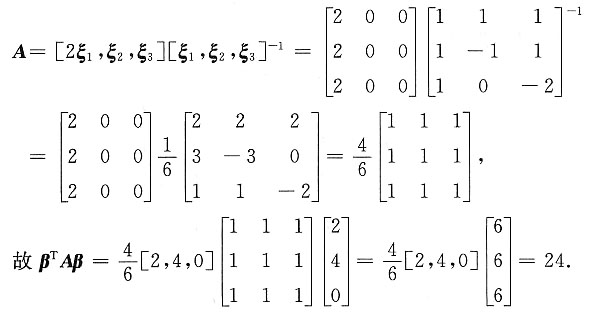
3. 设试验成功的概率为
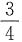
,失败的概率为
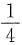
,独立重复试验直到成功两次为止.求试验次数的数学期望.
4. 计算
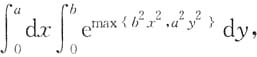
其中a,b>0.
解:
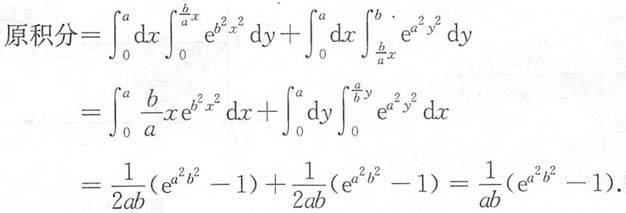
5. 设D={(x,y)|0≤x≤π,0≤y≤2},求

解:将D分成两块:
D
1={(x,y)|0≤x≤π,sinx≤y≤2},
D
2={(x,y)|0≤x≤π,0≤y≤sinx}.
所以
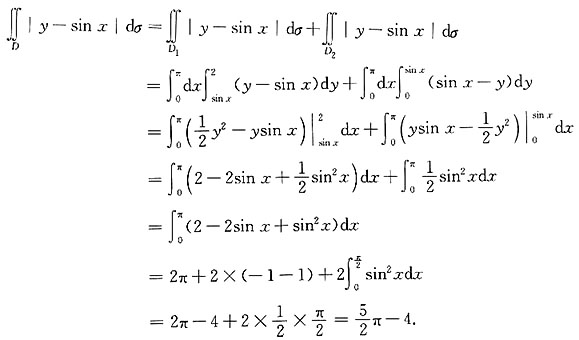
6. 设b>a>0,证明

证:原不等式
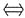
(a+b)(lnb-lna)-2(b-a)>0,将b改为x,则转化为函数不等式(a+x)(lnx-lna)-2(x-a)>0(x>a).
令F(x)=(a+x)(lnx-lna)-2(x-a)>0,x>a,则F(x)在[a,+∞)上二阶可导,且
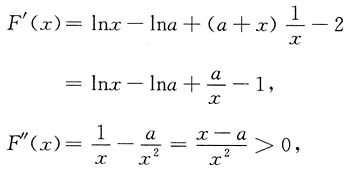
所以当x>a时,F'(x)单调增加,即
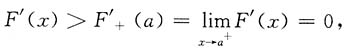
于是F(x)在[a,+∞)上单调增加,所以对b>a>0,有

即
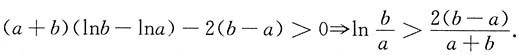
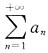 收敛,则
收敛,则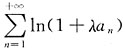 (λ>0为常数)______
(λ>0为常数)______ 收敛,故
收敛,故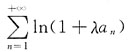 收敛.选A.
收敛.选A.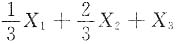
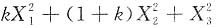

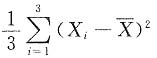
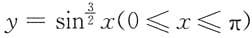 与x轴围成的图形绕x轴旋转所成旋转体的体积为______
与x轴围成的图形绕x轴旋转所成旋转体的体积为______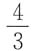
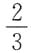
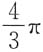
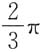
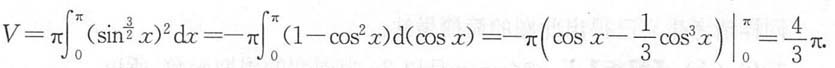
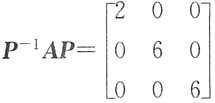 ,α1是矩阵A属于特征值λ=2的特征向量,α2,α3是矩阵A属于特征值λ=6的线性无关的特征向量,那么矩阵P不能是______
,α1是矩阵A属于特征值λ=2的特征向量,α2,α3是矩阵A属于特征值λ=6的线性无关的特征向量,那么矩阵P不能是______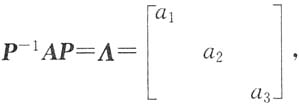 P=[α1,α2,α3],则有AP=PΛ.即
P=[α1,α2,α3],则有AP=PΛ.即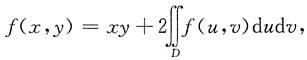 其中D:x2+y2=2x,则f(x,y)=______
其中D:x2+y2=2x,则f(x,y)=______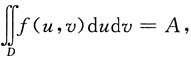 则f(x,y)=xy+2A,两边对x,y在D上积分,得
则f(x,y)=xy+2A,两边对x,y在D上积分,得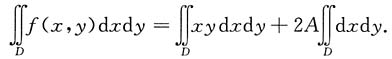
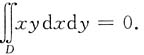 于是A=2Aπ,即A=0,故f(x,y)=xy.
于是A=2Aπ,即A=0,故f(x,y)=xy.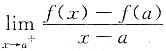 存在,于是
存在,于是 ,即f(x)在x=a处右连续,同理由f(x)在x=a处左可导,得f(x)在x=a处左连续,故f(x)在x=a处连续,由于左右导数不一定相等,选D.
,即f(x)在x=a处右连续,同理由f(x)在x=a处左可导,得f(x)在x=a处左连续,故f(x)在x=a处连续,由于左右导数不一定相等,选D.
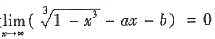 ,则______
,则______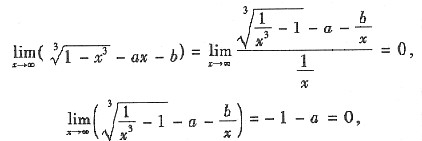
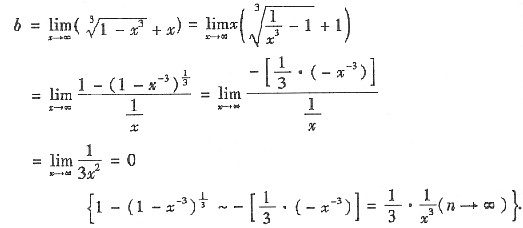
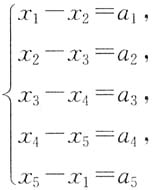 有解的充要条件是______.
有解的充要条件是______.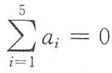
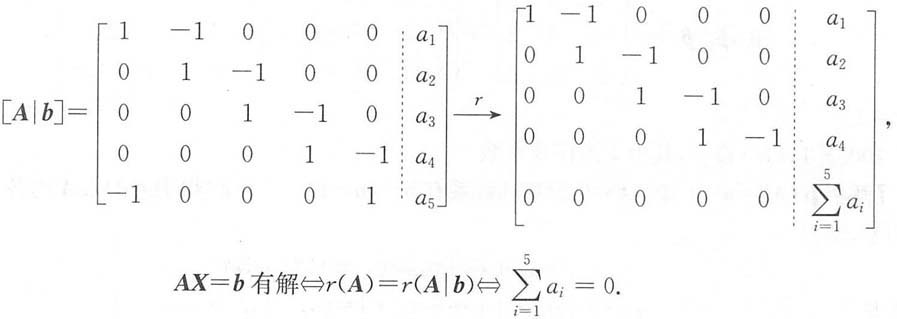
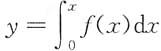 在(0,0)处的切线方程是______.
在(0,0)处的切线方程是______.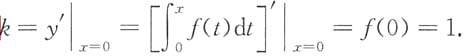 所以曲线在(0,0)处,切线方程为y=x.
所以曲线在(0,0)处,切线方程为y=x.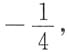 则(X,Y)的概率密度f(x,y)为______.
则(X,Y)的概率密度f(x,y)为______.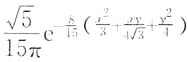
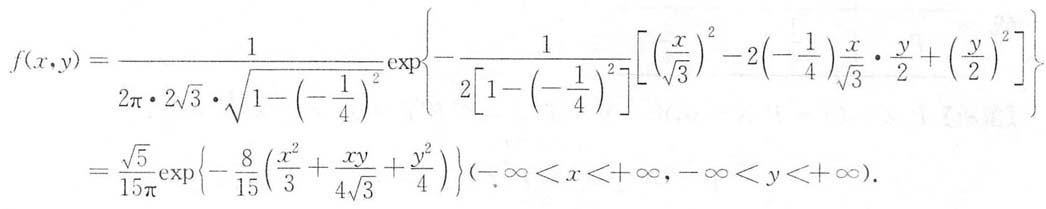
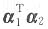 =a2-a+1-a=0,解得a=1.
=a2-a+1-a=0,解得a=1.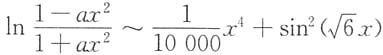 ,则a=______.
,则a=______.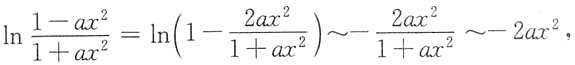
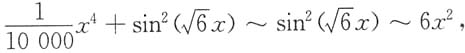 故a=-3.
故a=-3.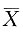 是样本均值,则
是样本均值,则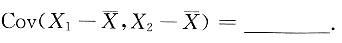
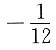
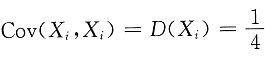 ,i=1,2,3.
,i=1,2,3.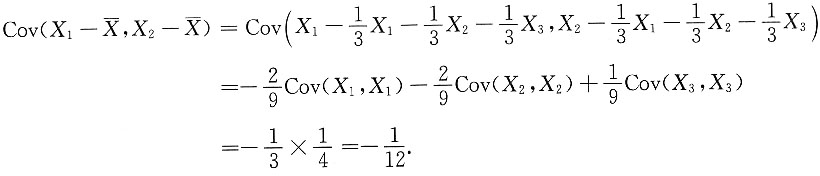
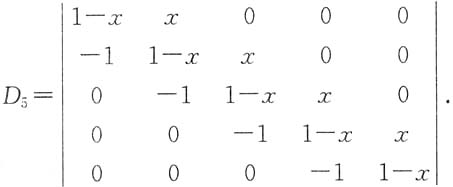
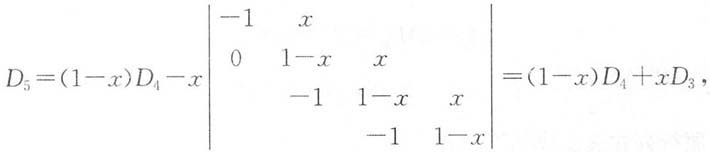
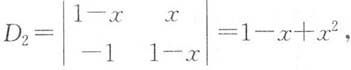 D1=1-x,于是得
D1=1-x,于是得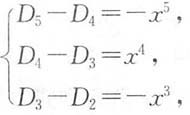
 A有λ1=2,对应的特征向量为
A有λ1=2,对应的特征向量为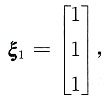 又r(A)=1,|A|=0,故A有特征值λ2=λ3=0(二重),对应λ2=λ3=0的特征向量设为ξ=[x1,x2,x3]T,则ξ和ξ1正交.
又r(A)=1,|A|=0,故A有特征值λ2=λ3=0(二重),对应λ2=λ3=0的特征向量设为ξ=[x1,x2,x3]T,则ξ和ξ1正交.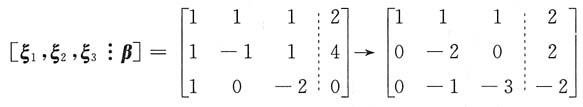
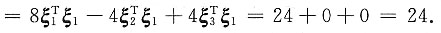
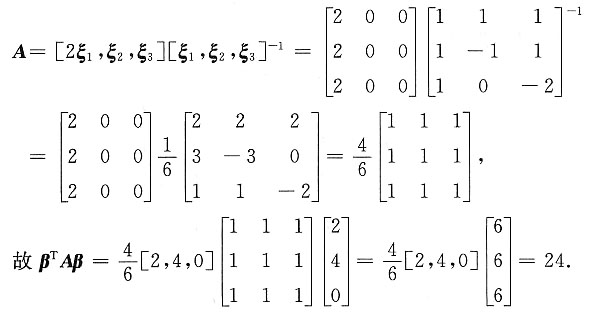
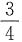 ,失败的概率为
,失败的概率为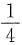 ,独立重复试验直到成功两次为止.求试验次数的数学期望.
,独立重复试验直到成功两次为止.求试验次数的数学期望.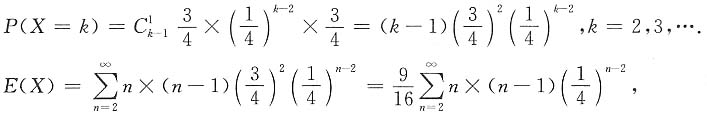
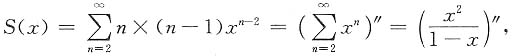
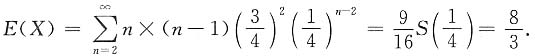
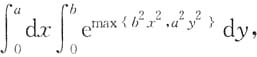 其中a,b>0.
其中a,b>0.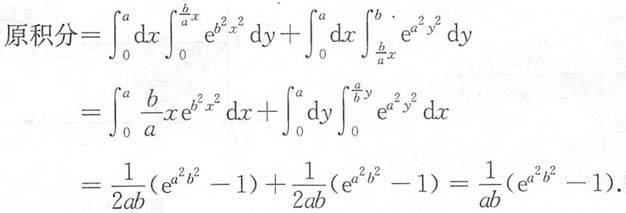

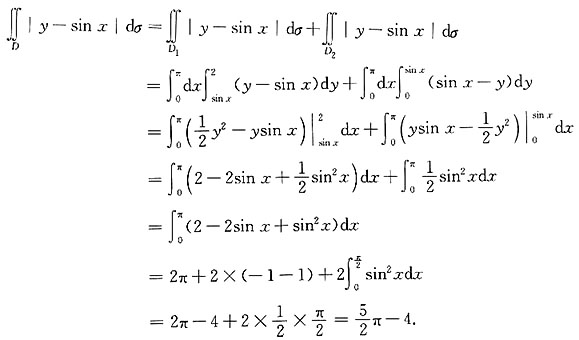

 (a+b)(lnb-lna)-2(b-a)>0,将b改为x,则转化为函数不等式(a+x)(lnx-lna)-2(x-a)>0(x>a).
(a+b)(lnb-lna)-2(b-a)>0,将b改为x,则转化为函数不等式(a+x)(lnx-lna)-2(x-a)>0(x>a).