第Ⅰ卷(选择题)
一、选择题(在每小题给出的四个选项中,只有一项是符合题目要求的)1. 已知f'(cosx)=sinx,则f(cosx)=______
A.-cosx+C
B.cosx+C
C.

D.

A B C D
C
[解析] 已知f'(cosx)=sinx,在此式两侧对cosx求积分,得

有

故选C.
2. 函数

在点x=0处连续,则k等于______
A.

B.0
C.

D.

A B C D
D
[考点] 分段函数在一点处的连续性.
[解析]

因为f(x)在x=0连续,所以

,即

.
7. 设f(0)=0,且f'(0)存在,则

=______.
A.f(0)
B.

C.f'(0)
D.2f'(0)
A B C D
D
[考点] 本题考查导数的定义.
[解析]

=2f'(0).
8. 设函数f(x)=

,在点x=0处可导,则______.
- A.a=0,b=0
- B.a=0,b=1
- C.a=1,b=0
- D.a=1,b=1
A B C D
B
[考点] 本题考查函数可导和连续的定义.
[解析] 由于函数f(x)在x=0处可导,因此在x=0处连续.由于
f(0
-)=

=

(ax+b)=b,f(0
+)=

=1,
由f(0
-)=f(0
+),可得b=1.又

由f'
-=f'
+(0),可得a=0.
提示 可导函数一定连续,但连续函数不一定可导,比如y=|x|,在x=0处连续,但不可导.
第Ⅱ卷(非选择题)
二、填空题1.
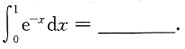
1-e-1
[解析] 解法一 利用凑微分法.

解法二 利用定积分换元法.
设t=-x,则dx=-dt.当x=0时,t=0;当x=1时,t=-1,因此

2. 设z=ln(x
2+xy),则dz=______.
[解析] 解法一 由于

.因此

解法二 直接求微分.对z=ln(x
2+xy)两端取微分,可得
dz=dln(x
2+xy)=

=

(2xdx+ydx+xdy)
=

3.

[考点] 洛必达法则.
[解析]

4. 设区域D由y轴,y=x,y=1所围成,则

[考点] 二重积分的计算.
[解析]

5. 微分方程

满足初始条件y|
x=1=0的特解为______.
[解析] 由一阶线性微分方程的通解公式有

由初始条件y|
x=1=0,得C=0,故所求特解为
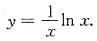
6. 过点(1,-1,0)且与平面2x-y+3z+1=0平行的平面方程为______.
2x-y+3z-3=0
[解析] 由于所求平面与已知平面2x-y+3z+1=0平行,因此所求平面的法向量可取为(2,-1,3).又所求平面过点(1,-1,0),由平面的点法式,可得所求平面方程为2(x-1)-(y+1)+3(x-0)=0,即2x-y+3z-3=0.
7. 设平面π的方程为x-y+2z=1,则过点A(2,-1,2)且与平面π垂直的直线方程为______.
[考点] 空间直线的标准方程.
[解析] 平面的法向量为{1,-1,2}.
所以直线方程为

8. 微分方程y'=y+2的通解为______.
y=Cex-2
[考点] 利用分离变量法求一阶微分方程的通解.
[解析] 分离变量可得
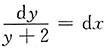
,两边同时积分得ln|y+2|=x+C
1,所以通解为y=Ce
x-2(C=±e
C1).
9.

,则b=______.
3ln5
[考点] 重要函数的极限.
[解析]

,所以

,即b=3ln5.
10. 曲线y=x
3-6x的拐点坐标为______.
(0,0)
[解析] 由y=x3-6x,得y'=3x2-6,y"=6x.令y"=0,得到x=0.
当x=0时,y=0.当x<0时,y"<0;当x>0时,y">0.
因此点(0,0)是曲线y=x3-6x的拐点.
三、解答题(共70分.解答应写出推理、演算步骤)1. 当x→∞时,f(x)与

为等价无穷小量,求

解 由于当x→∞时,f(x)与

为等价无穷小量,因此

[解析] 此极限是“∞·0”型,可用四则运算将其化成“

”,即

.再用等价无穷小量替换

2. 设
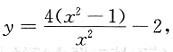
求所给曲线的水平渐近线与铅直渐近线.
解 由

可知y=2为水平渐近线;
由

可知x=0为铅直渐近线.
[解析] 解本题的关键是要知道函数y=f(x)的水平渐近线和铅直渐近线的判定方法.即:(1)如果
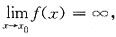
则称x=x
0是一条铅直渐近线;(2)如果

则称y=C是一条水平渐近线.
3. 计算

4. 将

展开为x的幂级数.
解 所给f(x)与标准展开级数中的形式不同,由于

因而

既有
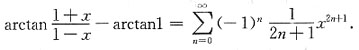
故

[解析]

不容易直接展开为幂级数形式.但是对其求导后所得函数,即

是常见函数,它的展开式是已知的.这样我们就得到f'(x)的幂级数展开式,然后对其两边积分,就可以得到f(x)的展开式.
5. 计算

.其中D是由y=x,x=0,y=1所围成的平面区域.
由区域D所围图形的特征可知,区域D既可看作X型区域,又可看作Y型区域.由于

不容易求得原函数,因此先对x积分,再对y积分,即把区域D看作Y型区域,所求二重积分会更容易求解.此时区域D可表示为
0≤x≤y,0≤y≤1.
则

6. 求

.
所求极限是

型,适合用洛必达法则求解.

提示 分子中的sinx不能用等价无穷小x替换.等价无穷小替换一般适用于乘积,而不适用于和差当中.
7. 计算
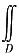
(x+y
2)dxdy,其中区域D由直线y=x,y=1与y轴围成.
由积分区域的图形特征以及被积函数的特征可知,积分区域D既可以表示成X型区域,又可以表示成Y型区域.
解法一 当积分区域看成X型区域时(即先对y积分,再对x积分),区域D可表示为
0≤x≤1, x≤y≤1.
因此
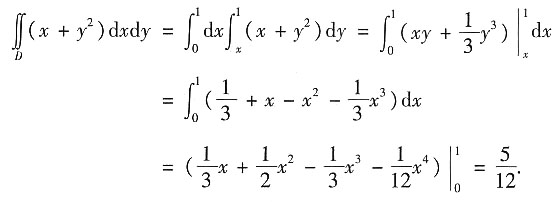
解法二 当积分区域看成Y型区域时(即先对x积分,再对y积分),区域D可表示为
0≤Y≤1,0≤x≤y.
因此
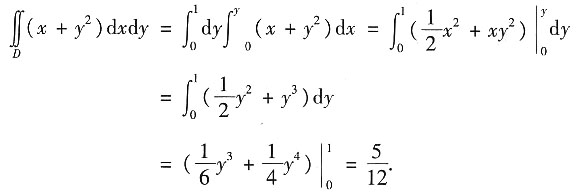
8. 欲围一个面积为150平方米的矩形场地,所用材料的造价其正面是每平方米6元,其余三面是每平方米3元.问场地的两边各为多少米时,才能使所用材料费最少?
解 设所围场地正面长为x,另一边为y,则xy=150,从而

设四面围墙高度相同,都是h,则四面围墙所使用的材料总费用为
f(x)=6xh+3(2yh)+3xh

则
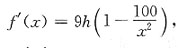
令f'(x)=0,得驻点x
1=10,x
2=-10(舍去).

f"(10)=1.8h>0.
由于驻点唯一,由实际意义可知最小值存在,因此可知当正面长为10米,侧面长为15米时所用材料费最少.
[解析] 先用其四个面的面积乘以相应的单位面积的造价,求和写出总费用函数f(x),然后用一元函数y=f(x)求最值法,即可得解.具体解法步骤如上.