第Ⅰ卷(选择题)
一、选择题(在每小题给出的四个选项中,只有一项是符合题目要求的)1. 若D为x
2+y
2≤1所确定的区域,则
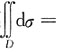
______
A B C D
B
[解析] 因为D:x
2+y
2≤1,所以此圆的面积S
D=1
2π=π.
所以
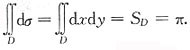
故选B.
3. 函数y=x
2-x+1在区间[-1,3]上满足拉格朗日中值定理的ξ等于______.
A.
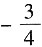
B.0
C.
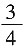
D.1
A B C D
D
[解析] 由于函数y=x2-x+1在区间[-1,3]上连续,在区间(-1,3)内可导,因此在[-1,3]上,y满足拉格朗日中值定理条件.又y'=2x-1,则存在ξ∈(-1,3),使得
f(3)-f(-1)=(2ξ-1)[3-(-1)],
即4(2ξ-1)=7-3,解得ξ=1.
4. 交换二次积分次序:
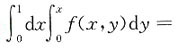
______
A.
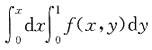
B.
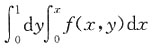
C.

D.

A B C D
C
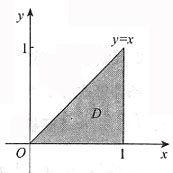
[解析] 由所给积分限可知积分区域D可以表示为:0≤x≤1,0≤y≤x,其图形如图所示.交换积分次序可得
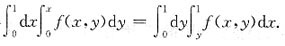
故选C.
7. 设
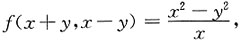
则f(x,y)=______
A.

B.
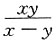
C.
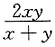
D.

A B C D
C
[解析]
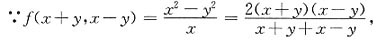
令x+y=u,x-y=v,则有f(u,v)=
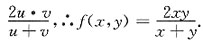
故选C.
第Ⅱ卷(非选择题)
二、填空题1. 设z=u
2·lnv,u=
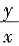
,v=
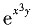
,则dz=______.
y3dx+3xy2dy
[解析] 将u=
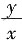
,v=

代入z=u
2·lnv,可得z=xy
3.因此
dz=d(xy
3)=y
3dx+3xy
2dy.
2. 设y=-f(x)是由方程x
3-y
3-3xy-9=0所确定的隐函数,则y'=______.
[解析] 解法一 将方程两端对x求导,可得3x
2-3y
2y'-3y-3xy'=0.
整理得 y'=
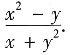
解法二 方程两端取微分,可得
d(x
3-y
3-3xy-9)=3x
2dx-3y
2dy-3(ydx+xdy)
=(3x
2-3y)dx-(3y
2+3x)dy=0.
因此 y'=
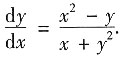
3. 设
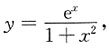
则y'=______.
[解析]

4. 函数
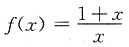
在[1,2]上符合拉格朗日中值定理的ξ=______.
[解析] 由拉格朗日中值定理有

解得ξ
2=2.
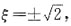
其中
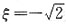
(舍),得
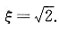
5. 设f(1)=1,
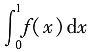
=1,则
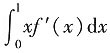
=______.
0
[考点] 本题是对利用分部积分法求定积分的考查.
[解析]
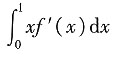
=

=f(1)-1-0.
6. 设z=2x
2y+cosy,则
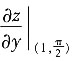
=______.
1
[解析] 由于
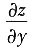
=2x
2-siny,因此
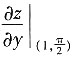
=1.
7. 已知f(0)=1,f(1)=2,f'(1)=3,则
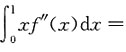
______.
2
[解析] 由题设有
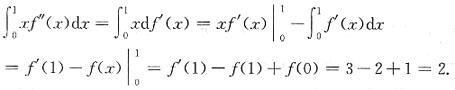
8. 过原点且与平面2x-y+3z+5=0平行的平面方程为______.
2x-y+3z=0
[解析] 已知平面π1:2x-y+3z+5=0的法向量n1={2,-1,3}.所求平面π∥π1,则平面π的法向量n∥n1,可以取n=n1={2,-1,3}.由于所求平面过原点,由平面的点法式方程,得2x-y+3z=0为所求平面方程.
9. 函数y=x
2-2x在区间[1,2]上满足拉格朗日中值定理条件的ξ=______.
[解析] 因为y=x
2-2x在[1,2]上满足拉格朗日中值定理的条件,
则设f(x)-x
2-2x,有
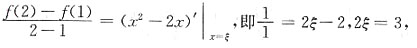
所以
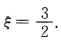
10.
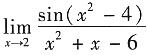
=______.
[解析] 所求极限为

型.遇到这种类型的题,先考虑用等价无穷小替换,然后再考虑用洛必达法则求解.