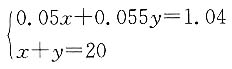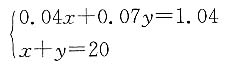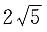一、问题求解(在每小题的五个选项中选择一项)
1. 已知点P(x,y)到A(0,4)与B(-2,0)的距离相等,则2
x+4
y的最小值为______.
A.2
B.4
C.

D.

E.

A B C D E
D
[解析] 因为点P(x,y)到A(0,4)与B(-2,0)的距离相等,所以点P(x,y)在AB的垂直平分线上.该垂直平分线过AB的中点(-1,2),k
AB=2,垂直平分线的斜率

.故垂直平分线的方程为x+2y-3=0,即x+2y=3.又因为2
x+4
y=2
x+2
2y,且2
x>0,2
2y>0,故

,故最小值为

综上所述,答案选择D.
4. 设A
1,A
2,A
3为三个独立事件,且P(A
k)=p(k=1,2,3;0<p<1),则这三个事件不全发生的概率是______.
- A.(1-p)3
- B.3(1-p)
- C.(1-p)3+3p(1-p)
- D.3p(1-p)2+3p2(1-p)
- E.3p(1-p)2
A B C D E
C
[解析] 事件A
1,A
2,A
3不全发生可表示为
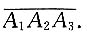
所以

各选项中,只有选项C,(1-P)
3+3P(1-p)=1-P
3.
故本题应选C.
5. 等差数列{a
n}中,a
5<0,a
6>0,且a
6>|a
5|,S
n是前n项之和,则______.
- A.S1,S2,S3均小于0,而S4,S5,…均大于0
- B.S1,S2,…,S5均小于0,而S6,S7,…均大于0
- C.S1,S2,…,S9均小于0,而S10,S11…均大于0
- D.S1,S2,…,S10均小于0,而S11,S12,…均大于0
- E.以上结论均不正确
A B C D E
C
[解析] 设等差数列{a
n}的首项为a
1,公差为d,根据题意,有
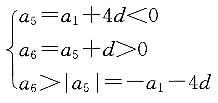
由此可得
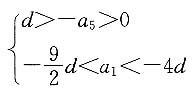
而
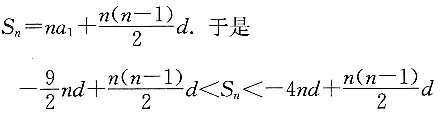
即
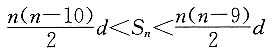
因此,当n≤9时,S
n<0;当n≥10时,S
n>0.
故本题应选C.
7. 已知等差数列{a
n}中,a
2+a
3+a
10+a
11=64,则S
12=______.
A B C D E
D
[解析] 由题设条件,有
a
2+a
3+a
10+a
11=(a
1+d)+(a
1+2d)+(a
1+9d)+(a
1+10d)
=4a
1+22d=64
所以,2a
1+11d=32,又
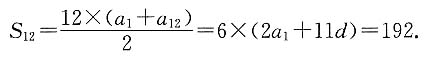
故本题应选D.
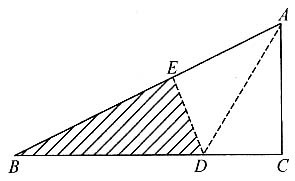
9. 直角三角形ABC的斜边AB=13厘米,直角边AC=5厘米.把AC对折到AB上去与斜边相重合,点C与点E重合,折痕为AD(如下图),则图中阴影部分的面积为______平方厘米.
A.20
B.14
C.
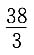
D.
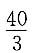
E.12
A B C D E
D
[解析] 由题意,
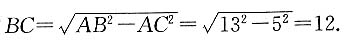
又△ABC∽△BDE,所以
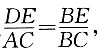
可得
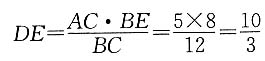
所以
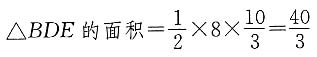
故本题应选D.
10. S
n是等差数列{a
n}的前n项和,且
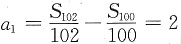
,则数列
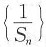
的前20项和为______.
A.
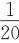
B.
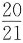
C.

D.
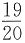
E.1
A B C D E
B
[解析] 等差数列基本问题
等差数列前n项和为
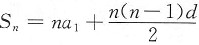
,
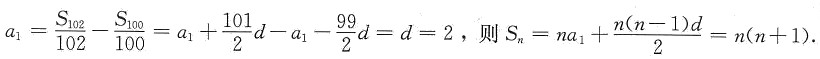
数列
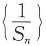
的通项公式为

,所以,
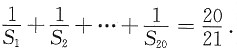
12. 已知实数k满足

,则k-2016
2=______.
A.2016
B.
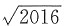
C.2017
D.2017
2 E.0
A B C D E
C
[解析] 非负性问题
由非负性得k-2017≥0,即k≥2017,
则
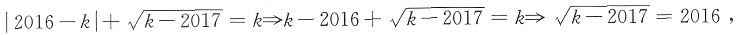
两边平方得,k-2016
2=2017.
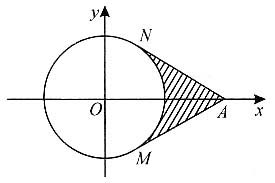
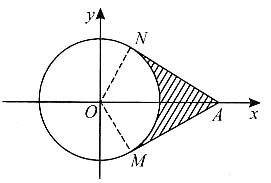
13. 过点A(2,0)向圆x
2+y
2=1作两条切线AM和AN(见下图),则两切线和弧MN所围成的面积(图中阴影部分)为______.
A.
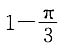
B.

C.
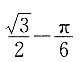
D.
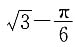
E.
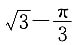
A B C D E
E
[解析] 如下图,连接OM,ON,则AN⊥ON,AM⊥OM.在△AON中,ON=1,AO=2,所以∠AON=60°.
类似可得∠AOM=60°.且
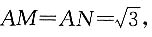
所以四边形ANOM的面积

故本题应选E.
二、条件充分性判断要求判断每题给出的条件(1)和条件(2)能否充分支持题干所陈述的结论。A、B、C、D、E五个选项为判断结果,请选择一项符合试题要求的判断。
- A.条件(1)充分,但条件(2)不充分.
- B.条件(2)充分,但条件(1)不充分.
- C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.
- D.条件(1)充分,条件(2)也充分.
- E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.
2.

(1)a,b均为实数,且|a
2-2|+(a
2-b
2-1)
2=0
(2)a,b均为实数,且
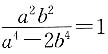
A B C D E
D
[解析] 由条件(1),有a
2-2=0,a
2-b
2=1.所以a
2=2,b
2=1.于是
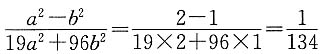
故条件(1)充分.
由条件(2),有a
2b
2=a
4-2b
4.即a
4-2b
4-a
2b
2=0
a
4-2b
4-a
2b
2=(a
2+b
2)(a
2-2b
2)=0
而a
2+b
2≠0,又有a
2-2b
2=0.于是,a
2=2b
2,且
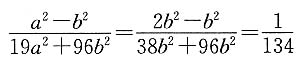
故条件(2)充分.
故本题应选D.
3. 一元二次方程kx
2-(2k+1)x+k+2=0有两个相异实根.
(1)
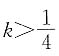
(2)-4<k≤-1
A B C D E
B
[解析] 方程kx
2-(2k+1)x+k+2=0有两个相异实根,只需判别式
Δ=(2k+1)
2-4k(k+2)=-4k+1>0.
解 得
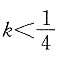
由条件(1),
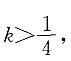
可知条件(1)不充分.
由条件(2),

故条件(2)充分.
故本题应选B.
6.
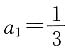
.
(1)在数列{a
n}中,a
3=2
(2)在数列{a
n}中,a
2=2a
1,a
3=3a
2 A B C D E
C
[解析] 条件(1)、(2)单独都不充分.当两个条件联合时,a
2=2a
1,a
3=3a
2=6a
1,所以6a
1=2,得
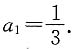
故本题应选C.
7. 已知α,β是方程3x
2-8x+a=0的两个非零实根,则a=2.
(1)α,β的几何平均值为2
(2)
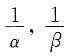
的算术平均值为2
A B C D E
B
[解析] 由已知条件,有

由条件(1),
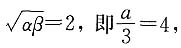
所以a=12.条件(1)不充分.
由条件(2),
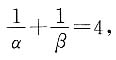
所以
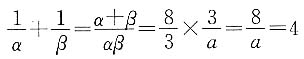
所以a=2.条件(2)充分.
故本题应选B.
8. x
2+y
2=41.
(1)
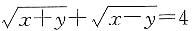
(2)x
2-y
2=9
A B C D E
C
[解析] 条件(1)、(2)单独都不充分.当两个条件联合时,条件(2)可写为
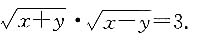
即有
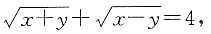
且
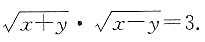
由此可知,
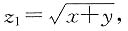
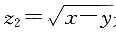
是方程z
2-4z+3=0的两根,不难求得方程的两根是1,3.于是,
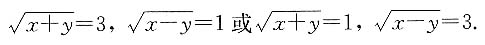
由
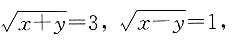
得x=5,y=4,所以x
2+y
2=41.
由
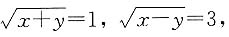
得x=5,y=-4,所以x
2+y
2=41.
故本题应选C.



 .故垂直平分线的方程为x+2y-3=0,即x+2y=3.又因为2x+4y=2x+22y,且2x>0,22y>0,故
.故垂直平分线的方程为x+2y-3=0,即x+2y=3.又因为2x+4y=2x+22y,且2x>0,22y>0,故 ,故最小值为
,故最小值为
 =b或a=c
=b或a=c 三角形是以a为腰的等腰三角形.
三角形是以a为腰的等腰三角形.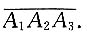 所以
所以
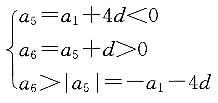
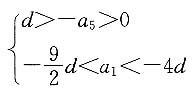
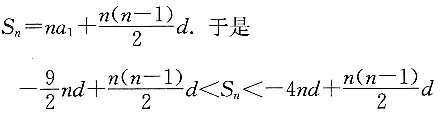
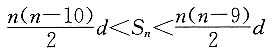

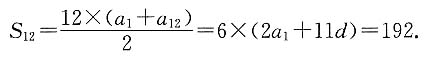
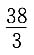
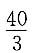
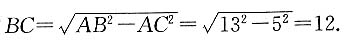
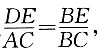 可得
可得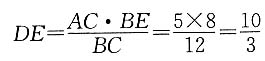
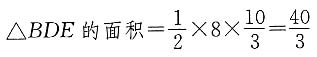
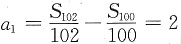 ,则数列
,则数列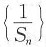 的前20项和为______.
的前20项和为______.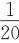
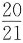

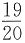
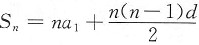 ,
,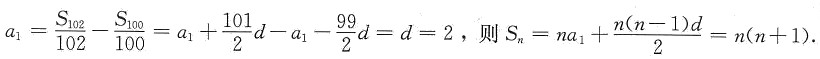
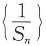 的通项公式为
的通项公式为 ,所以,
,所以,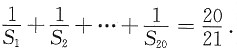
 ,则k-20162=______.
,则k-20162=______.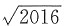
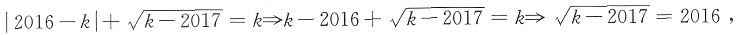
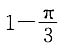

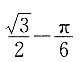
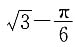
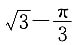
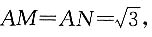 所以四边形ANOM的面积
所以四边形ANOM的面积
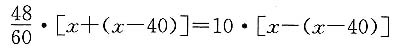 化简得8(x-20)=2000,解得x=270(米/分),x-40=230(米/分).
化简得8(x-20)=2000,解得x=270(米/分),x-40=230(米/分).
 .
.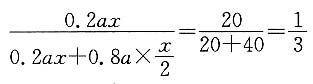

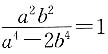
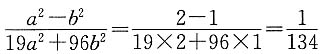
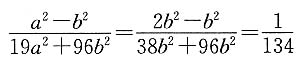
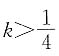 (2)-4<k≤-1
(2)-4<k≤-1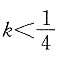
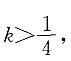 可知条件(1)不充分.
可知条件(1)不充分. 故条件(2)充分.
故条件(2)充分.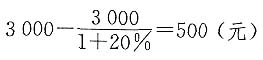
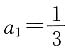 .
.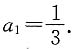
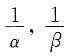 的算术平均值为2
的算术平均值为2 由条件(1),
由条件(1),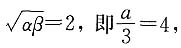 所以a=12.条件(1)不充分.
所以a=12.条件(1)不充分.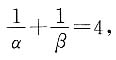 所以
所以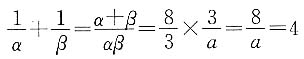
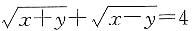
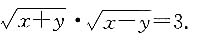 即有
即有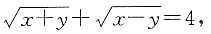 且
且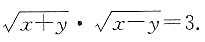 由此可知,
由此可知,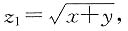
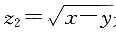 是方程z2-4z+3=0的两根,不难求得方程的两根是1,3.于是,
是方程z2-4z+3=0的两根,不难求得方程的两根是1,3.于是,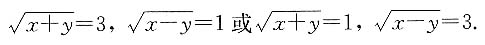
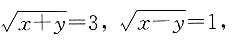 得x=5,y=4,所以x2+y2=41.
得x=5,y=4,所以x2+y2=41.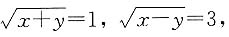 得x=5,y=-4,所以x2+y2=41.
得x=5,y=-4,所以x2+y2=41.