银符考试题库B12
现在是：
试卷总分：100.0
您的得分：
考试时间为：
点击“开始答卷”进行答题
交卷
评分
存入我的题库
晒成绩
打印模式
隐藏答案解析
打印
下载
背景
字体
较大
大
中
小
较小
退出
新疆维吾尔自治区教师公开招聘考试中学数学分类模拟15
一、选择题
1. 下列命题中，真命题是______
A．
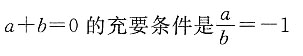
B．
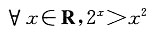
C．
D．a＞1，b＞1是ab＞1的充分条件
A
B
C
D
D
[解析]
所以A错；当x=2时，2
x
=x
2
，因此B错；a+b=0中b可取0，而
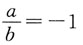
中b不可取0，因此，两者不等价，所以C错．
2. 函数y=f(2x-1)的定义域为(0，3)，则f(x
2
+1)的定义域为______．
A．(1，5)
B．
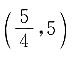
C．(1，10)
D．
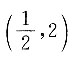
A
B
C
D
B
[解析] y=f(2x-1)的定义域为(0，3)，即0＜2x-1＜3，解得
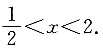
则
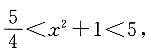
即f(x
2
+1)的定义域为
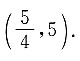
3. 设曲线
在点
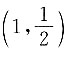
处的切线与直线ax+5y+1=0垂直，则a=______．
A．4
B．-4
C．
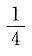
D．
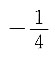
A
B
C
D
A
[解析]
是曲线
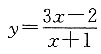
上的点，又因为
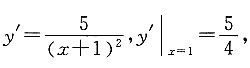
故在点
处切线的斜率为
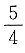
，又因为切线与直线ax+5y+1=0垂直，即
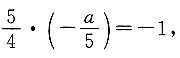
解得a=4．
4. 由0、1、2、3、4、5可以组成______个能被5整除且不含重复数字的五位数．
A.96
B.120
C.216
D.600
A
B
C
D
C
[解析] ①若组成五位数的数字中不包含0，即该五位数由1、2、3、4、5五个数字组成，则要想其能被5整除，则数字5须排在个位上，所以此时满足条件的五位数共有
个．②若组合成五位数的数字中包含0，如果其中不包含数字5，则0须排在个位上，故此时满足条件的五位数共有
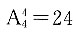
个；如果其中同时包含5，则当0在个位上时，共有
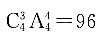
个，当0不在个位而5在个位时，共能组成
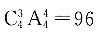
个数，其中0在万位上的有
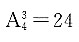
个，故此时满足条件的五位数共有
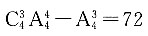
个．所以符合题干要求的五位数共有24+24+96+72=216个．
5. 下列关于用斜二测画法画直观图的说法不正确的是______
A.在实物图中取坐标系不同，所得的直观图有可能不同
B.平行于坐标轴的线段在直观图中仍然平行于坐标轴
C.平行于坐标轴的线段长度在直观图中仍然保持不变
D.斜二测坐标系中∠x'O'y'可以是135°
A
B
C
D
C
[解析] 根据斜二测画法的过程可知平行于x轴的线段长度不变，但是平行于y轴的线段长度减半，所以C错误，故选C．
6. 下列选项中说法错误的是______．
A.义务教育阶段的课程内容要反映社会的需求、数学的特点，要符合学生的认知规律
B.有效的教学活动是学生学和教师教的统一
C.教师教学要发挥主体作用，处理好讲授与学生自主学习的关系
D.评价既要关注学生学习的结果，也要重视学习的过程
A
B
C
D
C
[解析] 教师教学要发挥主导作用而不是主体作用，学生才是教学的主体．因此C项错误．
7. 下列四个说法：①对立事件一定是互斥事件；②A，B为两个事件，则P(A∪B)=P(A)+P(B)；③若事件A，B，C两两互斥，则P(A)+P(B)+P(C)=1；④若事件A，B满足P(A)+P(B)=1，则A，B互为对立事件．其中错误说法的个数是______
A.0个
B.1个
C.2个
D.3个
A
B
C
D
D
[解析] ②当A，B互斥时，才有P(A∪B)=P(A)+P(B)；③事件A，B，C两两互斥，其并事件并不一定是必然事件；④事件A：掷一枚硬币，正面向上，事件B：掷一枚骰子，出现奇数点，则
但A，B不互为对立事件，故②③④错误，选D．
8. 从3名女同学和2名男同学中选1人主持本班的某次主题班会，则不同的选法种数为______
A.6
B.5
C.3
D.2
A
B
C
D
B
[解析] 完成这件事即选出一人做主持人，可分选女主持人和选男主持人两类进行，分别有3种选法和2种选法，所以共有3+2=5种不同的选法．
9. 设P={x|x＜1}，Q={x|x
2
＜4}，则P∩Q=______
A.{x|-1＜x＜2}
B.{x|-3＜x＜-1}
C.{x|1＜x＜4}
D.{x|-2＜x＜1}
A
B
C
D
D
[解析] 集合Q中由x
2
＜4可得-2＜x＜2，又∵P中x＜1，即
故选D．
10. 实数
中，无理数的个数是_______.
A.2
B.3
C.4
D.5
A
B
C
D
A
[解析]本题主要考查无理数的概念．
判断一个数是否是无理数的条件就是看这个数是否是无限不循环小数，0.9是循环小数，是有理数；故只有
是无理数，选A项．
二、填空题
1. 已知a=-2i+2j，b=-mi+j，c=4i+nj是平面内的三个向量，若此三向量共线，则m+n=______．
-3
[解析] 根据题意知a=(-2，2)，b=(-m，1)，c=(4，n)，因为三向量共线，所以
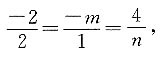
解得m=1，n=-4，所以m+n=-3．
2. 函数(1+x)ln(1-2x)在x=0处的x的幂级数展开式为______．
[解析] 因为
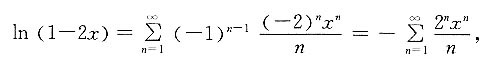
则
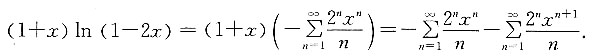
3. 设集合A为有n个元素的有限集合，则A的子集个数为______，真子集的个数为______，非空子集个数为______．
2
n
2
n
-1 2
n
-1
[解析] 子集的个数：
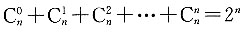
；真子集即不包括集合A本身的子集，则个数为2
n
-1；非空子集即不包括空集，个数也为2
n
-1．
4. 在平面直角坐标系xOy中，曲线C
1
和C
2
的参数方程分别为
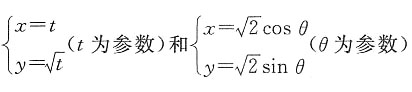
，则曲线C
1
与C
2
的交点坐标为______．
(1，1)
[解析] C
1
与C
2
的普通方程分别为：x=y
2
(y≥0)和x
2
+y
2
=2，联立方程解得
5. 已知a⊥b，|a|=2，|b|=4，则|a+b|______|a-b|．(填“＞”“＜”或“=”)
=
[解析] 依题意知a·b=0，所以
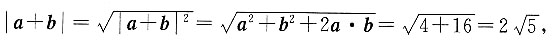
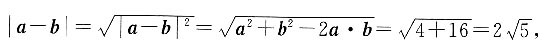
所以|a+b|=|a-b|．
三、解答题
某食品企业一个月内被消费者投诉的次数用ξ表示，据统计，随机变量ξ的概率分布如下：
ξ
0
1
2
3
P
0.1
0.3
2a
a
1. 求a的值和ξ的数学期望；
由概率分布的性质有0.1+0.3+2a+a=1，解得a=0.2，所以ξ的概率分布列为
ξ
0
1
2
3
P
0.1
0.3
0.4
0.2
所以Eξ=0×0.1+1×0.3+2×0.4+3×0.2=1.7.
2. 假设一月份与二月份被消费者投诉的次数互不影响，求该企业在这两个月内共被消费者投诉2次的概率．
设事件A表示“两个月内共被投诉2次”，事件A
1
表示“两个月内有一个月被投诉2次，另外一个月被投诉0次”，事件A
2
表示“两个月内每月均被投诉1次”．则由事件的独立性得P(A
1
)=2×0.4×0.1=0.08；P(A
2
)=0.3×0.3=0.09，
所以P(A)=P(A
1
)+P(A
2
)=0.084.0.09=0.17，故该企业在这两个月内共被消费者投诉2次的概率为0.17.
3. 求过点
且与平面a
1
：x+y+z+1=0和平面a
2
：2x+y-z+2=0都平行的直线方程．
设所求直线的方向向量为s=(m，n，p)，
平面α
1
：x+y+z+1=0的一个法向量为n
1
=(1，1，1)，
平面α
2
：2x+y-z+2=0的一个法向量为n
2
=(2，1，-1)．
因为所求直线与两个平面都平行，则直线的方向向量与两平面的法向量均垂直，取
所以所求直线的方程为
4. 求
的展开式中有理项的系数和．
原式展开式的通项为
当r=0或3或6时，即第一项、第四项与第七项为有理项，
所以有理项的系数和为1-160+64=-95．
在正方形ABCD中，边长为4cm，点P从B点向C点运动，点Q从C点向D点运动．点P运动的速度是点Q运动速度的2倍．P点运动的速度为1cm/s，△PCQ的面积为y．
5. 求时间t与y的函数关系；
根据图象可知，
所以
6. 哪一时刻△PCQ的面积最大，最大值为多少?
因为
故当t=2时，y取最大值，即△PCQ的面积最大为1cm
2
．
所以当t=2时，△PCQ的面积最大，为1cm
2
．
7. 已知
，最小正周期为π，
时取得最大值为
，求函数的解析式．
已知函数最小正周期为π，ω＞0，由
得ω=2．
因为
时取得最大值
，且
所以
当k=0时，
则
所以该函数的解析式
一、选择题
1
2
3
4
5
6
7
8
9
10
二、填空题
1
2
3
4
5
三、解答题
1
2
3
4
5
6
7
深色：已答题 浅色：未答题
提交纠错信息
评价难易度
提交知识点
所以A错；当x=2时，2x=x2，因此B错；a+b=0中b可取0，而
中b不可取0，因此，两者不等价，所以C错．
则
即f(x2+1)的定义域为
在点
处的切线与直线ax+5y+1=0垂直，则a=______．
是曲线
上的点，又因为
故在点
处切线的斜率为
，又因为切线与直线ax+5y+1=0垂直，即
解得a=4．
个．②若组合成五位数的数字中包含0，如果其中不包含数字5，则0须排在个位上，故此时满足条件的五位数共有
个；如果其中同时包含5，则当0在个位上时，共有
个，当0不在个位而5在个位时，共能组成
个数，其中0在万位上的有
个，故此时满足条件的五位数共有
个．所以符合题干要求的五位数共有24+24+96+72=216个．
但A，B不互为对立事件，故②③④错误，选D．
故选D．
中，无理数的个数是_______.
是无理数，选A项．
解得m=1，n=-4，所以m+n=-3．
则
；真子集即不包括集合A本身的子集，则个数为2n-1；非空子集即不包括空集，个数也为2n-1．
，则曲线C1与C2的交点坐标为______．
所以|a+b|=|a-b|．
且与平面a1：x+y+z+1=0和平面a2：2x+y-z+2=0都平行的直线方程．
的展开式中有理项的系数和．
，最小正周期为π，
时取得最大值为
，求函数的解析式．
得ω=2．
时取得最大值
，且
深色：已答题 浅色：未答题