二、填空题把答案填在题中横线上1.
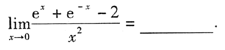
1.
[提示] 用洛必达法则求极限.请读者注意:含有指数函数的
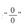
型不定式极限,建议读者用洛必达法则求解,不容易出错!
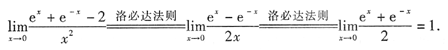
2.
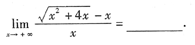
0
[分析] 本题考查的知识点是极限的计算.由于分子是“∞-∞”,应首先有理化,再消去“∞”因子.本题若直接用洛必达法则求解反而比较麻烦。
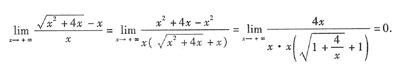
本题也可以直接消去“∞”因子:
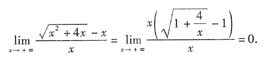
3. 函数
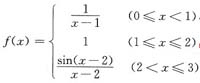
,的连续区间为______.
[0,1)∪(1,3]
[分析] ∵在x=1处,
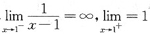
,∴x=1处f(x)不连续.
在x=2处,∵
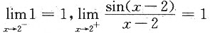
,f(2)=1,
∴在x=2处f(x)连续,所以连续区间为[0,1)∪(1,3].
4.

5. 若f(x)在x=a处可导,则
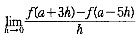
=______.
8f'(a)
[精析精解] ∵f(x)在x=a处可导
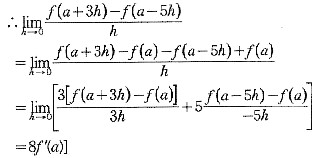
6. 已知
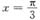
是
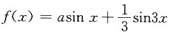
的极值点,则a=______.
7.

8. 设
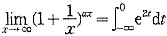
,则常数a=______.
-ln2
[精析精解]
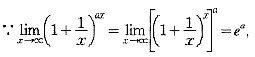
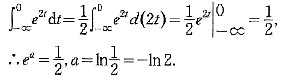
9.

10. 设袋中有10个球,其中6个白球,4个黄球,从中任取2个球(设每个球取到的可能性相同),则取出的2个球是1个白球、1个黄球的概率P=______.
[分析] 取出的2个球是1个白球,1个黄球,意味着从6个白球中取1个,从4个黄球中取1个,其取法种数为

,则此事件的概率为
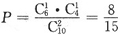
.