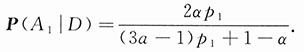解答题1. 已知男子有5%是色盲患者,女子有0.25%是色盲患者.今从男女人数相等的人群中随机地挑选一人,恰好是色盲者,问此人是男性的概率是多少?
解:以A表示事件“选出的是男性”,则
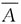
表示事件“选出的是女性”,以H表示事件“选出的人患色盲”,则
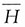
表示“选出的人不患色盲”。由题设
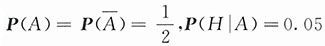
,
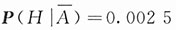
,所需求的概率是P(A|H).由贝叶斯公式得
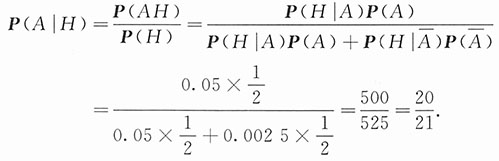
[考点] 概率论的基本概念
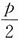 .
.2. 若至少有一次及格则他能取得某种资格,求他取得该资格的概率.
解:以A
i表示事件“第i次考试及格”,i=1,2;以A表示“他能取得某种资格”.
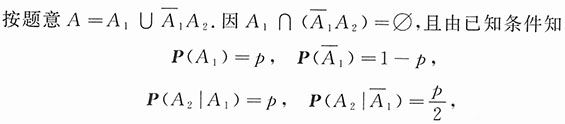
故
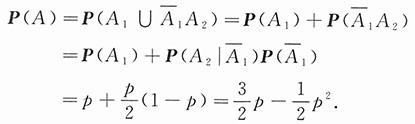
[考点] 概率论的基本概念
3. 若已知他第二次已经及格,求他一次及格的概率.
解:
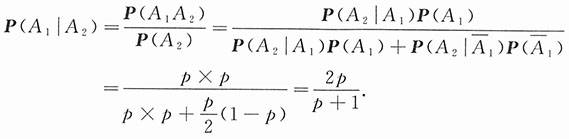
[考点] 概率论的基本概念
4. 将两信息分别编码为A和B传送出去,接收站收到时,A被误收作B的概率为0.02,而B被误收作A的概率为0.01.信息A与信息B传送的频繁程度为2:1.若接收站收到的信息是A,问原发信息是A的概率是多少?
解:以D表示事件“将信息A传递出去”,则
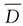
表示事件“将信息B传递出去”,以R表示“接收到信息A”,则
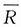
表示事件“接收到信息B”,按题意需求概率P(D|R).已知
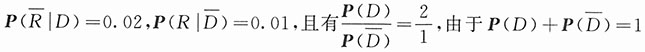
,得知
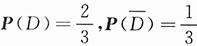
.由贝叶斯公式得
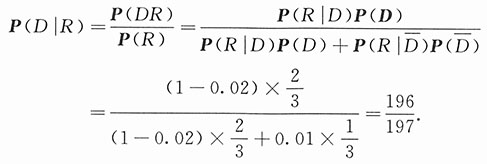
[考点] 概率论的基本概念
5. 第一次取到的零件是一等品的概率.
解:以H表示事件“从第一箱中取零件”,则
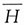
表示事件“从第二箱中取零件”.由已知条件
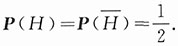
又以A
i表示事件“第i次从箱中(不放回抽样)取得的是一等品”,i=1,2.
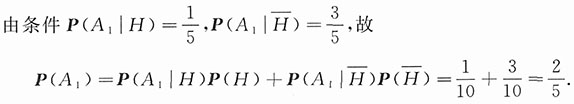
[考点] 概率论的基本概念
6. 第一次取到的零件是一等品的条件下,第二次取到的也是一等品的概率.
解:
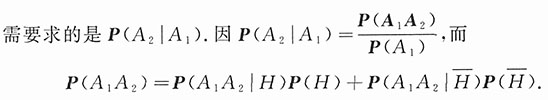
由条件概率的含义,P(A
1A
2|H)表示在第一箱中取两次,每次取一只产品,作不放回抽样,且两次都取得一等品的概率.因第一箱共有50只产品,其中有10只一等品,故有
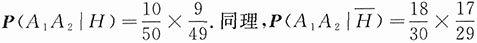
,故有
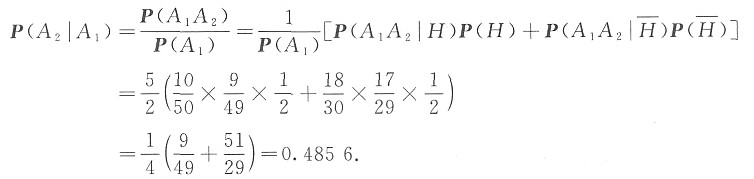
[考点] 概率论的基本概念
7. 某人下午5:00下班.他所积累的资料见表所列:
| 到家时间 | 5:35~5:39 | 5:40~5:44 | 5:45~5:49 | 5:50~5:54 | 迟于5:54 |
| 乘地铁的概率 | 0.10 | 0.25 | 0.45 | 0.15 | 0.05 |
| 乘汽车的概率 | 0.30 | 0.35 | 0.20 | 0.10 | 0.05 |
某日他抛一枚硬币决定乘地铁还是乘汽车,结果他是5:47到家的.试求他是乘地铁回家的概率.
解:以H表示事件“乘地铁回家”,则
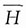
表示事件“乘汽车回家”.因到家时间为5:47,它属于区间5:45~5:49,以T记“到家时间在5:45~5:49之间”,则需要求的是概率P(H|T).已知P(T|H)=0.45,
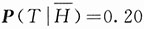
,又因他是由掷硬币决定乘地铁还是乘汽车,因此,
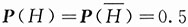
.由贝叶斯公式得
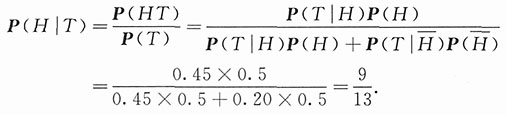
[考点] 概率论的基本概念
8. 求主人回来树还活着的概率.
解:记A为事件“树还活着”,记W为事件“邻居记得给树浇水”,即有
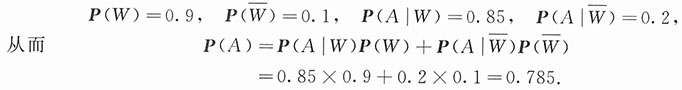
[考点] 概率论的基本概念
9. 若主人回来树已死去,求邻居忘记浇水的概率.
解:
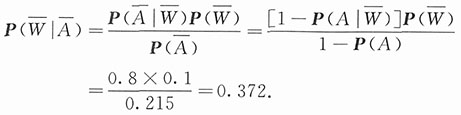
[考点] 概率论的基本概念
10. 已知P(A)>0,证明P(AB|A)≥P(AB|A∪B).
证明:若P(A)>0,要证P(AB|A)≥P(AB|A∪B).
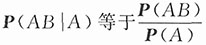
,而
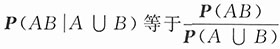
.因为

,P(A∪B)≥P(A),故有P(AB|A∪B)≤P(AB|A).
[考点] 概率论的基本概念
11. 若P(A|B)=1,证明
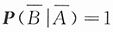
.
证明:由P(A|B)=1得
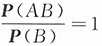
,即
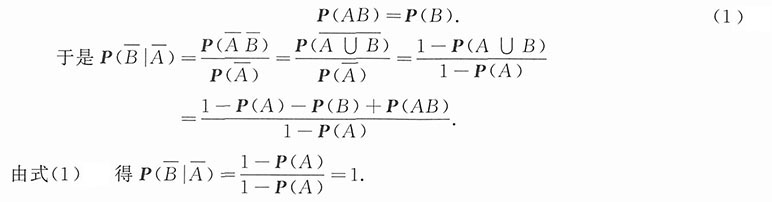
[考点] 概率论的基本概念
12. 若设C也是事件,且有P(A|C)≥P(B|C),
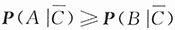
,证明P(A)≥P(B).
证明:由假设P(A|C)≥P(B|C),可得
P(AC)≥P(BC). (2)
同样由
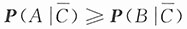
可得

由式(3)P[A(S-C)]≥P[B(S-C)],得
P(A)-P(AC)≥P(B)-P(BC),或P(A)-P(B)≥P(AC)-P(BC),
由式(2),得P(A)-P(B)≥0,即P(A)≥P(B).
[考点] 概率论的基本概念
13. 这两颗花籽都能发芽的概率.
解:以A,B分别表示事件第一颗、第二颗花籽能发芽,即有P(A)=0.8,P(B)=0.9.
由A,B相互独立,得两颗花籽都能发芽的概率为
P(AB)=P(A)P(B)=0.8×0.9=0.72.
[考点] 概率论的基本概念
14. 至少有一颗能发芽的概率.
解:至少有一颗花籽能发芽的概率,即事件A∪B的概率为
P(A∪B)=P(A)+P(B)-P(AB)=0.8+0.9-0.72=0.98.
[考点] 概率论的基本概念
15. 恰有一颗能发芽的概率.
解:恰有一颗花籽能发芽的概率,即为事件

的概率,

[考点] 概率论的基本概念
16. B型的人只有输入B,O两种血型才安全.若妻为B型,夫为何种血型未知,求夫是妻的安全输血者的概率.
解:由题意知夫血型应为B,O才为安全输血者.因两种血型互不相容,故所求概率
p1=0.44+0.13=0.57.
[考点] 概率论的基本概念
17. 随机地取一对夫妇,求妻为B型夫为A型的概率.
解:因夫妻拥有血型相互独立,于是所求概率为
p2=0.13×0.37=0.0481.
[考点] 概率论的基本概念
18. 随机地取一对夫妇,求其中一人为A型,另一人为B型的概率.
解:p3=2×0.37×0.13=0.0962.
[考点] 概率论的基本概念
19. 随机地取一对夫妇,求其中至少有一人是O型的概率.
解:有三种可能,即夫为O,妻为非O;妻为O,夫为非O;夫妻均为O,则所求概率为
p4=2×0.44×(1-0.44)+0.44×0.44=0.6864.
[考点] 概率论的基本概念
20. 给出事件A、B的例子,使得
(ⅰ)P(A|B)<P(A),(ⅱ)P(A|B)=P(A),(ⅲ)P(A|B)>P(A).
解:举例:
(ⅰ)设试验为将骰子掷一次,事件A为“出现偶数点”,B为“出现奇数点”,则
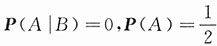
,故P(A|B)<P(A).
(ⅱ)设试验为将骰子掷一次,事件A为“出现偶数点”,事件B为“掷出点数≥1”,则
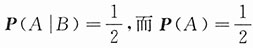
.故P(A|B)=P(A).
(ⅲ)设试验为将骰子掷一次,事件A为“出现偶数点”,事件B为“掷出点数≥4”,则
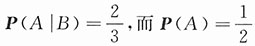
,故P(A|B)>P(A).
[考点] 概率论的基本概念
21. 设事件A,B,C相互独立,证明(ⅰ)C与AB相互独立;(ⅱ)C与A∪B相互独立.
解:因A,B,C相互独立,故P(AB)=P(A)P(B),P(BC)=P(B)P(C),P(CA)=P(C)P(A),P(ABC)=P(A)P(B)P(C),从而
(ⅰ)P[C(AB)]=P(CAB)=P(C)P(A)P(B)=P(C)P(AB),即C与AB相互独立.
(ⅱ)P[C(A∪B)]=P(CA∪CB)=P(CA)+P(CB)-P(CAB)
=P(C)P(A)+P(C)P(B)-P(C)P(A)P(B)
=P(C)[P(A)+P(B)-P(AB)]一P(C)P(A∪B),
这表示C与A∪B相互独立.
[考点] 概率论的基本概念
22. 设事件A的概率P(A)=0,证明对于任意另一事件B,有A,B相互独立.
解:因
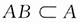
,故若P(A)=0,则0≤P(AB)≤P(A).从而
P(AB)=0=P(B)·0=P(B)·P(A),
按定义,A,B相互独立.
[考点] 概率论的基本概念
23. 证明事件A,B相互独立的充要条件是
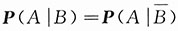
.
证明:充分性.设A,B相互独立,则

也相互独立,从而知P(A|B)=P(A),
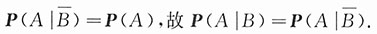
必要性.设
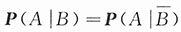
,按定义此式即表示
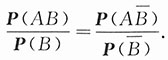
由比例的性质得
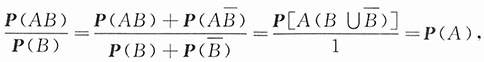
即P(AB)=P(A)P(B),从而可知A,B相互独立.
[考点] 概率论的基本概念
24. 若A与B互不相容,则它们相互独立.
解:必然错.因若A,B互不相容,则0=P(AB)≠P(A)P(B).
[考点] 概率论的基本概念
25. 若A与B相互独立,则它们互不相容.
解:必然错.因若A,B相互独立,则P(AB)=P(A)P(B)>0.
[考点] 概率论的基本概念
26. P(A)=P(B)=0.6,且A,B互不相容.
因为A,B互不相容,则P(A∪B)=P(A)+P(B)=1.2,这是错误的.
[考点] 概率论的基本概念
27. P(A)=P(B)=0.6,且A,B相互独立.
28. 有一种检验艾滋病毒的检验法,其结果有概率0.005报道为假阳性.(即不带艾滋病毒者,经此检验法有0.005的概率被认为带艾滋病毒).今有140名不带艾滋病毒的正常人全部接受此种检验,被报道至少有一人带艾滋病毒的概率为多少?
解:在本题中,这140人检查结果是相互独立的,这一假定是合理的.将人编号,第i号人检验结果以A
i表示正常,则
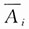
表示被报道为带艾滋病毒者.由题意知
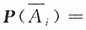
0.005,从而P(A
i)=1-0.005=0.995.于是140人经检验至少有一人被报道呈阳性概率为
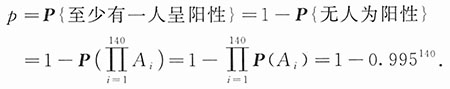
由140lg0.995=lg0.4957,得
p=1-0.4957=0.5043.
这说明,即使无人带艾滋病毒,这样的检验法认为140人中至少有一人带艾滋病毒的概率大于
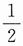
.
[考点] 概率论的基本概念
29. 盒中有编号为1,2,3,4的4只球,随机地自盒中取一只球,事件A为“取得的是1号或2号球”,事件B为“取得的是1号或3号球”,事件C为“取得的是1号或4号球”,验证:
P(AB)=P(A)P(B),P(AC)=P(A)P(C),P(BC)=P(B)P(C),
但P(ABC)≠P(A)P(B)P(C),
即事件A,B,C两两独立,但A,B,C不是相互独立的.
证明:以A
i(i=1,2,3,4)表示取到第i号球,则
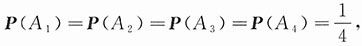
又A=A
1∪A
2,B=A
1∪A
3,C=A
1∪A
4,且A
1,A
2,A
3,A
4两两互不相容,故有
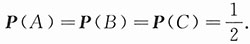
另外,AB=A
1,AC=A
1,BC=A
1,ABC=A
1,故
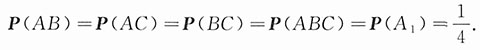
从而有
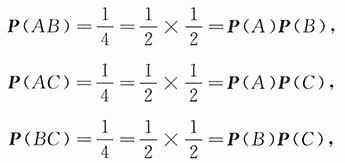
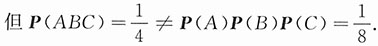
[考点] 概率论的基本概念
30. 设有4个独立工作的元件1,2,3,4.它们的可靠性分别为p
1,p
2,p
3,p
4,将它们按图1(a)所示的方式联接(称为并串联系统);
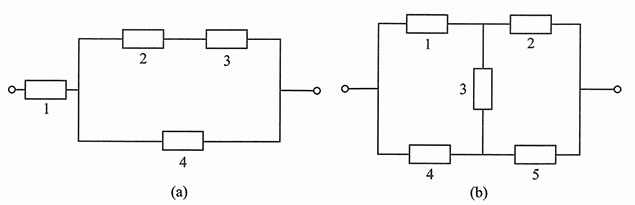 图1
图1
解:以Ai表示事件“第i只元件正常工作”,i=1,2,3,4,以A表示“系统正常工作”,已知各元件是否正常工作相互独立,且有P(Ai)=pi(i=1,2,3,4).由图1(a)可知
A=A1[(A2A3)∪A4]=A1A2A3∪A1A4.
由加法公式及各元件工作的独立性得到
P(A)=P(A1A2A3)+P(A1A4)-P[(A1A2A3)∩(A1A4)]
=P(A1)P(A2)P(A3)+P(A1)P(A4)-P(A1A2A3A4)
=p1p2p3+p1p4-P(A1)P(A2)P(A3)P(A4)
=p1(p4+p2p3-p2p3p4).
[考点] 概率论的基本概念
31. 设有5个独立工作的元件1,2,3,4,5.它们的可靠性均为p,将它们按图1(b)所示的方式联接(称为桥式系统).试分别求这两个系统的可靠性.
解:以A
i表示事件“第i只元件正常工作”,i=1,2,3,4,5,以A表示“系统正常工作”,已知各元件是否正常工作相互独立,且有P(A
i)=p(i=1,2,3,4,5).
全概率公式法.按元件3处于正常工作与失效两种状态,将原系统简化为典型的并串联和串并联系统,再用全概率公式:
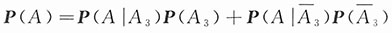
来计算原系统的可靠性.
当元件3正常工作时,系统简化成如图2(a)所示;当元件3失效时,系统简化成如图2(b)所示.因此
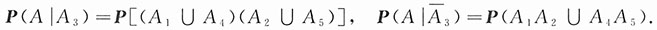
故
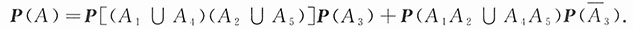
注意到P(A
1∪A
4)=P(A
1)+P(A
4)-P(A
1A
4)=2p-p
2.
同理P(A
2∪A
5)=2p-p
2.
所以P(A
1A
2∪A
4A
5)=P(A
1)P(A
2)+P(A
4)P(A
5)-P(A
1)P(A
2)P(A
4)P(A
5)
=2p
2-p
4.
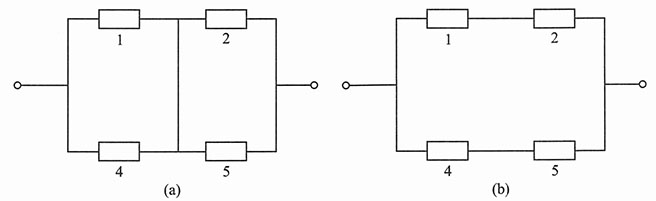 图2
图2 即得原系统的可靠性为
P(A)=(2p-p
2)
2p+(2p
2-p
4)(1-p)=2p
2+2p
3-5p
4+2p
5.
[考点] 概率论的基本概念
32. 如果一危险情况C发生时,一电路闭合并发出警报,我们可以借用两个或多个开关并联以改善可靠性.在C发生时这些开关每一个都应闭合,且若至少一个开关闭合了,警报就发出.如果两个这样的开关并联联接,它们每个具有0.96的可靠性(即在情况C发生时闭合的概率),问这时系统的可靠性(即电路闭合的概率)是多少?如果需要有一个可靠性至少为0.9999的系统,则至少需要用多少只开关并联?设各开关闭合与否是相互独立的.
解:以A
i表示事件“第i只开关闭合”,i=1,2,…,n.已知P(A
i)=0.96,由此可得两只这样的开关并联而电路闭合的概率为(注意各开关闭合与否是相互独立的).
P(A
1∪A
2)=P(A
1)+P(A
2)-P(A
1A
2)=P(A
1)+P(A
2)-P(A
1)P(A
2)
=2×0.96-0.96
2=0.9984.

要使R≥0.9999,即要使1-0.04
n≥0.9999,亦即要使0.0001≥0.04
n.故应有

因n为整数,故应有n≥3,即至少要用3只开关并联.
[考点] 概率论的基本概念
33. 三人独立地去破译一份密码,已知各人能译出的概率分别为
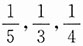
.问三人中至少有一人能将此密码译出的概率是多少?
解:以A
i表示事件“第i人能译出密码”,i=1,2,3.已知
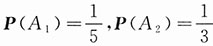
,
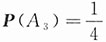
,则至少有一人能译出密码的概率为
p=P(A
1∪A
2∪A
3)
=P(A
1)+P(A
2)+P(A
3)-P(A
1A
2)-P(A
1A
3)-P(A
2A
3)+P(A
1A
2A
3).
由独立性即得
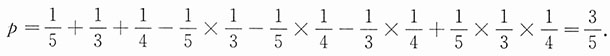
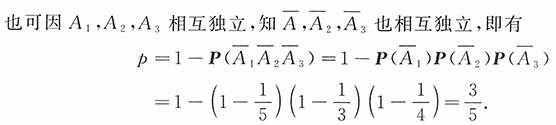
[考点] 概率论的基本概念
34. 求至少有一只蓝球的概率.
解:以B
i记事件“从第i只盒子中取得一只蓝球”,以W
i记事件“从第i只盒子中取得一只白球”,i=1,2.由题设在不同盒子中取球是相互独立的.
即需求P(B
1∪B
2).利用对立事件来求较方便,即有
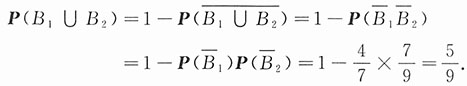
[考点] 概率论的基本概念
35. 求有一只蓝球一只白球的概率.
解:即需求事件B
1W
2∪B
2W
1的概率.注意到B
1,W
1是互不相容的,即
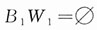
,因而
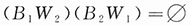
,故有
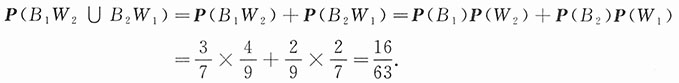
[考点] 概率论的基本概念
36. 已知至少有一只蓝球,求有一只蓝球一只白球的概率.
解:即需求条件概率p=P(B
1W
2∪B
2W
1|B
1∪B
2).因
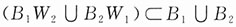
,故有
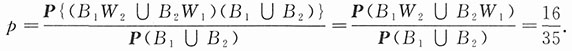
[考点] 概率论的基本概念
37. 袋中装有m枚正品硬币、n枚次品硬币(次品硬币的两面均印有国徽),在袋中任取一枚,将它投掷r次,已知每次都得到国徽.问这枚硬币是正品的概率为多少?
解:以T记事件“将硬币投掷r次每次都出现国徽”,以A记事件“所取到的是正品”,由题设
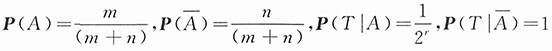
,需要求的是概率P(A|T).由贝叶斯公式,所求概率为
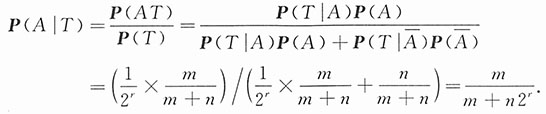
[考点] 概率论的基本概念
38. 设根据以往记录的数据分析,某船只运输的某种物品损坏的情况共有三种:损坏2%(这一事件记为A
1),损坏10%(事件A
2),损坏90%(事件A
3),且知P(A
1)=0.8,P(A
2)=0.15,P(A
3)=0.05.现在从已被运输的物品中随机地取3件,发现这3件都是好的(这一事件记为B).试求P(A
1|B),P(A
2|B),P(A
3|B)(这里设物品件数很多,取出一件后不影响取后一件是否为好品的概率).
解:在被运输的物品中,随机取3件,相当于在物品中抽取3次,每次取一件,作不放回抽样.又根据题中说明抽取一件后,不影响取后一件是否为好品的概率,已知当A
1发生时.一件产品是好品的概率为1-2%=0.98,从而随机取3件,它们都是好品的概率为0.98
3,即
P(B|A
1)=0.98
3,
同样P(B|A
2)=0.9
3,P(B|A
3)=0.1
3.
又知P(A
1)=0.8,P(A
2)=0.15,P(A
3)=0.05.
现在
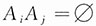
,i≠j,i,j=1,2,3,且P(A
1∪A
2∪A
3)=P(A
1)+P(A
2)+P(A
3)=1,由贝叶斯公式得

[考点] 概率论的基本概念
39. 将A,B,C三个字母之一输入信道,输出为原字母的概率为α,而输出为其他一字母的概率都是
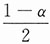
.今将字母串AAAA,BBBB,CCCC之一输入信道,输入AAAA,BBBB,CCCC的概率分别为p
1,p
2,p
3(p
1+p
2+p
3=1),已知输出为ABCA,问输入的是AAAA的概率是多少?(设信道传输各个字母的工作是相互独立的.)
解:以A
1、B
1、C
1分别表示事件“输入AAAA”“输入BBBB”“输入CCCC”,以D表示事件“输出ABCA”.因事件A
1,B
1,C
1两两互不相容,且有P(A
1∪B
1∪C
1)=P(A
1)+P(B
1)+P(C
1)=p
1+p
2+p
3=1,因此全概率公式和贝叶斯公式均可使用.由贝叶斯公式得

在输入为AAAA(即事件A
1)、输出为ABCA(即事件D)时,有两个字母为原字母,另两字母为其他字母,所以
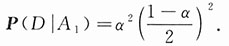
同理
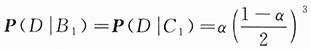
.代入式(1-4)并注意到p
1+p
2+p
3=1,得到
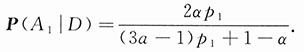
[考点] 概率论的基本概念
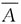 表示事件“选出的是女性”,以H表示事件“选出的人患色盲”,则
表示事件“选出的是女性”,以H表示事件“选出的人患色盲”,则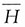 表示“选出的人不患色盲”。由题设
表示“选出的人不患色盲”。由题设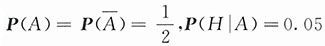 ,
,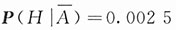 ,所需求的概率是P(A|H).由贝叶斯公式得
,所需求的概率是P(A|H).由贝叶斯公式得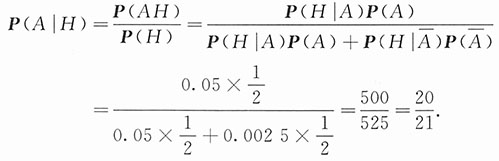
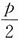 .
.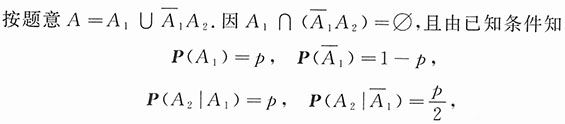
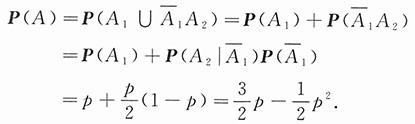
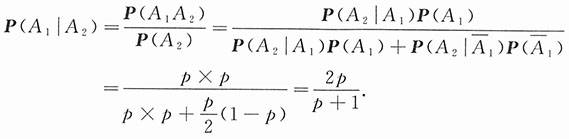
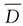 表示事件“将信息B传递出去”,以R表示“接收到信息A”,则
表示事件“将信息B传递出去”,以R表示“接收到信息A”,则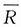 表示事件“接收到信息B”,按题意需求概率P(D|R).已知
表示事件“接收到信息B”,按题意需求概率P(D|R).已知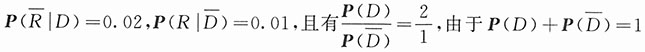 ,得知
,得知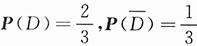 .由贝叶斯公式得
.由贝叶斯公式得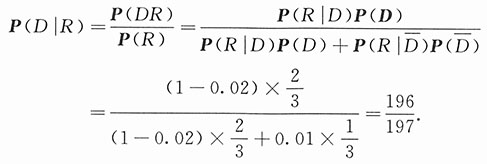
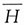 表示事件“从第二箱中取零件”.由已知条件
表示事件“从第二箱中取零件”.由已知条件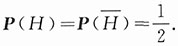 又以Ai表示事件“第i次从箱中(不放回抽样)取得的是一等品”,i=1,2.
又以Ai表示事件“第i次从箱中(不放回抽样)取得的是一等品”,i=1,2.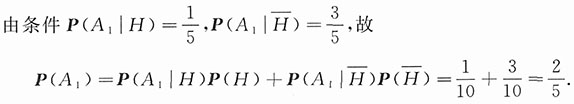
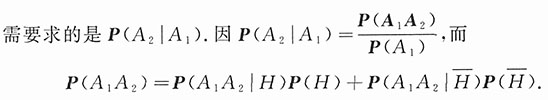
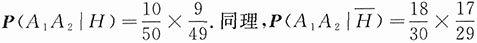 ,故有
,故有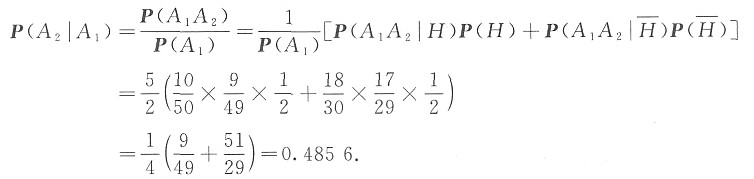
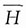 表示事件“乘汽车回家”.因到家时间为5:47,它属于区间5:45~5:49,以T记“到家时间在5:45~5:49之间”,则需要求的是概率P(H|T).已知P(T|H)=0.45,
表示事件“乘汽车回家”.因到家时间为5:47,它属于区间5:45~5:49,以T记“到家时间在5:45~5:49之间”,则需要求的是概率P(H|T).已知P(T|H)=0.45,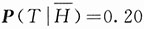 ,又因他是由掷硬币决定乘地铁还是乘汽车,因此,
,又因他是由掷硬币决定乘地铁还是乘汽车,因此,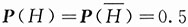 .由贝叶斯公式得
.由贝叶斯公式得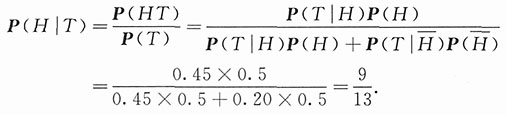
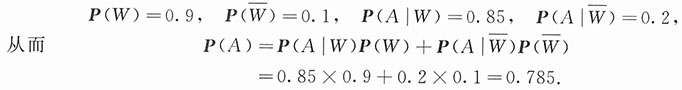
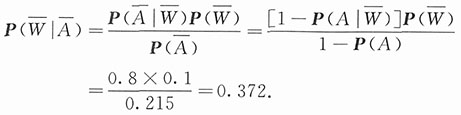
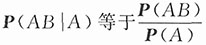 ,而
,而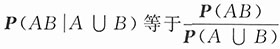 .因为
.因为 ,P(A∪B)≥P(A),故有P(AB|A∪B)≤P(AB|A).
,P(A∪B)≥P(A),故有P(AB|A∪B)≤P(AB|A).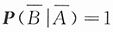 .
.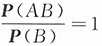 ,即
,即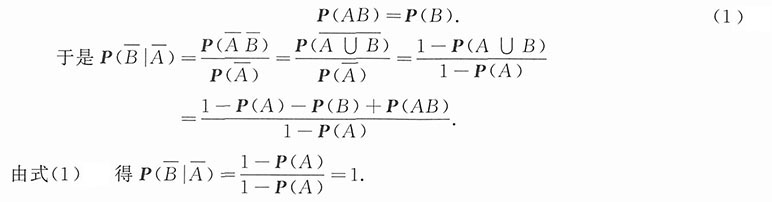
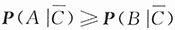 ,证明P(A)≥P(B).
,证明P(A)≥P(B).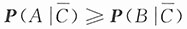 可得
可得
 的概率,
的概率,
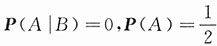 ,故P(A|B)<P(A).
,故P(A|B)<P(A).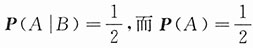 .故P(A|B)=P(A).
.故P(A|B)=P(A).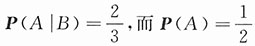 ,故P(A|B)>P(A).
,故P(A|B)>P(A).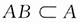 ,故若P(A)=0,则0≤P(AB)≤P(A).从而
,故若P(A)=0,则0≤P(AB)≤P(A).从而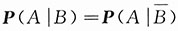 .
. 也相互独立,从而知P(A|B)=P(A),
也相互独立,从而知P(A|B)=P(A),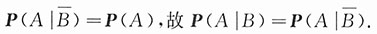
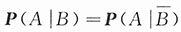 ,按定义此式即表示
,按定义此式即表示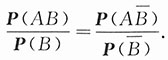
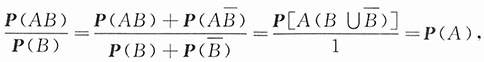
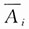 表示被报道为带艾滋病毒者.由题意知
表示被报道为带艾滋病毒者.由题意知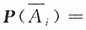 0.005,从而P(Ai)=1-0.005=0.995.于是140人经检验至少有一人被报道呈阳性概率为
0.005,从而P(Ai)=1-0.005=0.995.于是140人经检验至少有一人被报道呈阳性概率为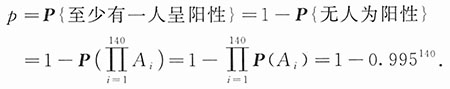
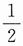 .
.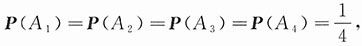
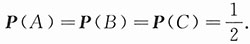
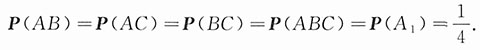
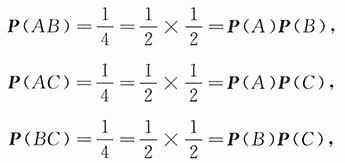
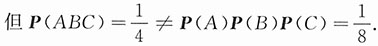

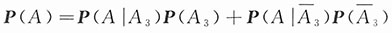
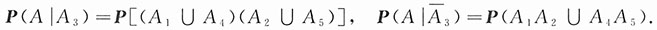
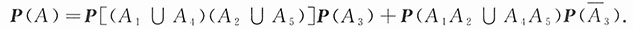



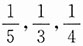 .问三人中至少有一人能将此密码译出的概率是多少?
.问三人中至少有一人能将此密码译出的概率是多少?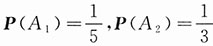 ,
,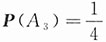 ,则至少有一人能译出密码的概率为
,则至少有一人能译出密码的概率为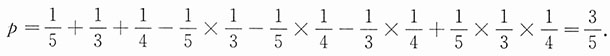
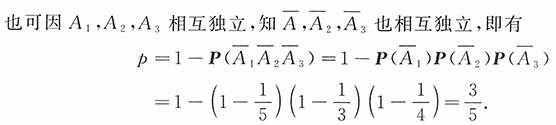
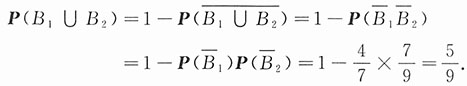
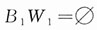 ,因而
,因而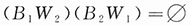 ,故有
,故有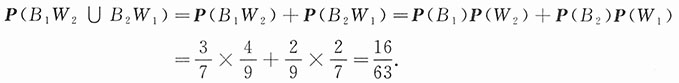
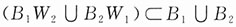 ,故有
,故有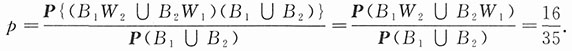
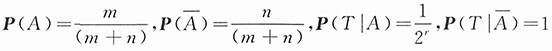 ,需要求的是概率P(A|T).由贝叶斯公式,所求概率为
,需要求的是概率P(A|T).由贝叶斯公式,所求概率为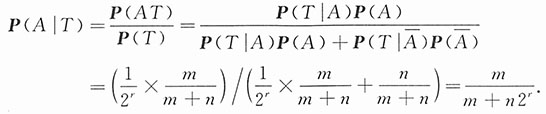
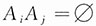 ,i≠j,i,j=1,2,3,且P(A1∪A2∪A3)=P(A1)+P(A2)+P(A3)=1,由贝叶斯公式得
,i≠j,i,j=1,2,3,且P(A1∪A2∪A3)=P(A1)+P(A2)+P(A3)=1,由贝叶斯公式得
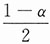 .今将字母串AAAA,BBBB,CCCC之一输入信道,输入AAAA,BBBB,CCCC的概率分别为p1,p2,p3(p1+p2+p3=1),已知输出为ABCA,问输入的是AAAA的概率是多少?(设信道传输各个字母的工作是相互独立的.)
.今将字母串AAAA,BBBB,CCCC之一输入信道,输入AAAA,BBBB,CCCC的概率分别为p1,p2,p3(p1+p2+p3=1),已知输出为ABCA,问输入的是AAAA的概率是多少?(设信道传输各个字母的工作是相互独立的.)
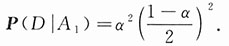
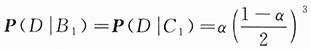 .代入式(1-4)并注意到p1+p2+p3=1,得到
.代入式(1-4)并注意到p1+p2+p3=1,得到