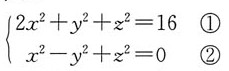单项选择题(每题的备选项中,只有一个最符合题意)2. 设
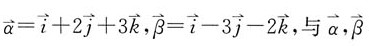
都垂直的单位向量为______。
A.
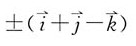
B.
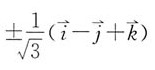
C.
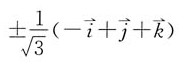
D.
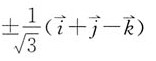
A B C D
D
[解析] 解:利用向量积求出与
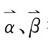
都垂直的向量,
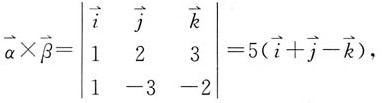
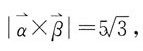
因单位的量
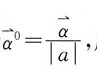
所以
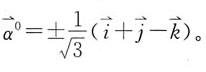
3. 设λ
1=6,λ
2=λ
3=3为三阶实对称矩阵A的特征值,属于λ
2=λ
3=3的特征向量为ξ
2=(-1,0,1)
T,ξ
3=(1,2,1)
T,则属于λ
1=6的特征向量是:______
- A.(1,-1,1)T
- B.(1,1,1)T
- C.(0,2,2)T
- D.(2,2,0)T
A B C D
A
[考点] 线性代数
[解析] 实对称矩阵其不同特征值对应的特征向量之间必定互相正交。由题意得,属于特征值λ1=6所对应的特征向量ξ1必定和λ2和λ3所对应的特征向量即ξ2和ξ3分别正交,故有ξ1·ξ2=ξ1·ξ3=0,代入选项只有A满足。
13. 设函数z=f(x,y)有连续的偏导数,且y=x
2时,有f(x,y)=1和
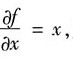
则
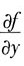
=______
A.

B.-2
C.1
D.0
A B C D
A
[考点] 考查复合函数的求导.
[解析] 将y=x
2代入f(x,y)=1中对x求偏导得:
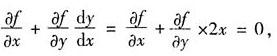
,代入
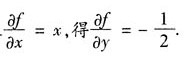
16. 波长λ=550nm(1nm=10
-9m)的单色光垂直入射于光栅常数为2×10
-4cm的平面衍射光栅上,可能观察到光谱线的最大级次为:______
A B C D
B
[考点] 光学
[解析] 光栅公式 dsinθ=±kλ (k=1,2,3,…)
在波长、光栅常数不变的情况下,要使k最大,sinθ必最大,取sinθ=1,此时,d=±kλ,
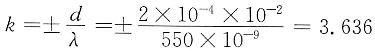
,取整后可得最大级次为3。
17. 整流滤波电路如图所示,已知U
1=30V,U
0=12V,R=2kΩ,R
L=4kΩ,稳压管的稳定电流I
zmin=5mA与I
zmax=18mA,通过稳压管的电流和通过二极管的平均电流分别是______。
- A.5mA,2.5mA
- B.8mA,8mA
- C.6mA,2.5mA
- D.6mA,4.5mA
A B C D
D
[解析] 解:该电路为全波整流、稳压电路,其中电容C上的电压为直流量,可以认为电容电流为零;整流二极管中的电流为电阻R中电流的1/2。
22. 设参数方程

确定了y是x的函数,且f'(t)存在,f(0)=2,f'(0)=2,则当t=0时,
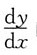
的值等于______。
A.
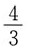
B.
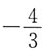
C.-2
D.2
A B C D
D
[解析] 解:
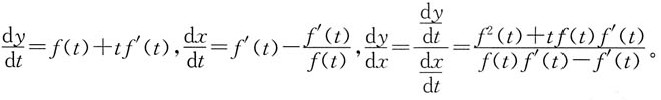
将t=0,f(0)=2,f'(0)=2代入得:
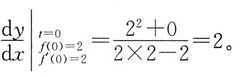
23. 在波长为λ的驻波中,两个相邻的波腹之间的距离为______
A.
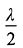
B.
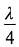
C.
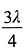
D.λ
A B C D
A
[解析] 相邻的两个波节(或波腹)之间的距离等于半个波长,即
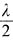
。
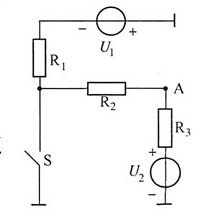
24. 如图所示电路中,已知:U
1=U
2=12V,R
1=R
2=4kΩ,R
3=16kΩ。S断开后A点电位U
AO和S闭合后A点电位U
AS分别是______。
- A.-4V,3.6V
- B.6V,0V
- C.4V,-2.4V
- D.-4V,2.4V
A B C D
D
[解析] 解:当开关S开时,电阻R1、R2、R3为串联,当开关S闭合时,电位可以R1、R2电阻分压决定。
28. 设a=3i-j-2k,b=i+2j-k,则cos(a,b)为______
A.
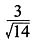
B.
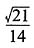
C.3
D.
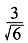
A B C D
B
[解析] 由a·b=|a||b|cos(a,b),得
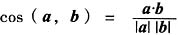
,其中:a·b=a
xb
x+a
yb
y+a
zb
z=3×1+(-1)×2+(-2)×(-1)=3,
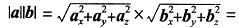
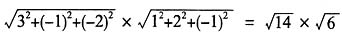
。因此,
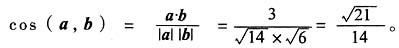
29. 某温度下,下列反应的平衡常数的关系是______。
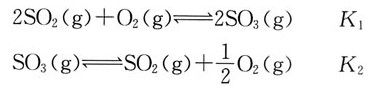
A.K
1=K
2 B.
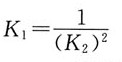
C.(K
2)
2=K
1 D.K
2=2K
1 A B C D
B
[解析] 解:反应方程式1为反应方程式2的逆反应乘以2。
根据多重平衡规则,
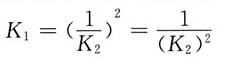
31. 一惰性电极电解一段时间后,pH增大的溶液为______
- A.HCl
- B.H2SO4
- C.Na2SO4
- D.NaHSO4
A B C D
A
[考点] 考查溶液的pH.
[解析] 写出电解反应方程式,若电解后的溶液中[H
+]减小或[OH
-]增加,则pH增大.A项,H
+得电子,Cl
-失电子,
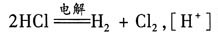
降低,pH增大;B项,H
+得电子,OH
-失电子,相当于电解
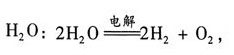
溶液的体积减小,[H
+]升高,pH变小;C项,相当于电解H
2O,pH不变;D项,相当于电解
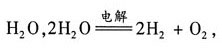
溶液的体积减小,
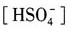
升高,[H
+]升高,pH变小.
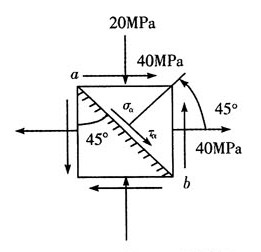
35. 图中立方体边长为a,场强分量为
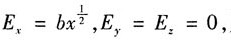
则立方体内的总电荷为______
A.
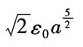
B.
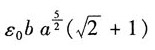
C.
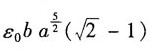
D.
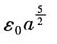
A B C D
C
[考点] 考查高斯定律.
[解析] 因为只有E
x分量,所以立方体只有S
1、S
2面有分量;则有:
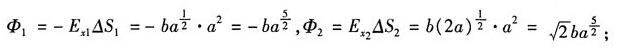
可得:
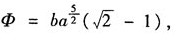
又知,
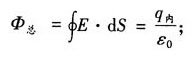
因此,得:
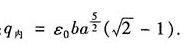
37. 已知二次型
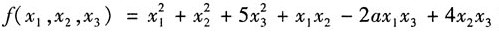
为正定的,则a的值为______
A.
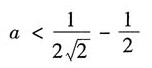
B.
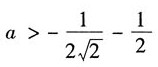
C.
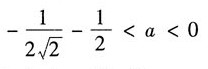
D.
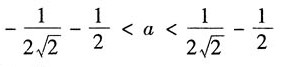
A B C D
D
[考点] 考查二次型.
[解析] 由二次型方程得到二次型的对称矩阵A为:
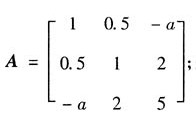
若二次型为正定的,则A的各阶主子式为正,因此,1>0;

计算得:
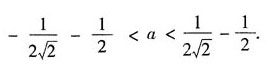
38. 设y=ln(cosx),则微分dy等于______
A.
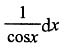
B.cotxdx
C.-tanxdx
D.
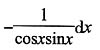
A B C D
C
[解析] y=lncosx,
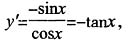
dy=-tanxdx。
40. 母线平行x轴且通过曲线
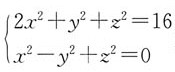
的柱面方程是______。
- A.椭圆柱面3x2+2z2=16
- B.椭圆柱面x2+2y2=16
- C.双曲柱面3y2-z2=16
- D.抛物柱面3y2-z=16
A B C D
C
[解析] 解:
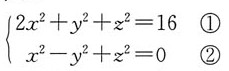
消x,由②×2得2x
2-2y
2+2z
2=0 ③
①-③得3y
2-z
2=16
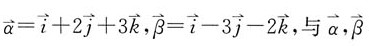 都垂直的单位向量为______。
都垂直的单位向量为______。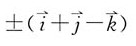
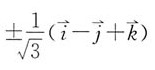
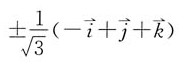
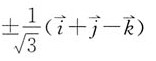
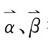 都垂直的向量,
都垂直的向量,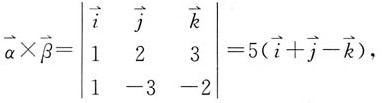
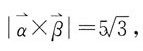 因单位的量
因单位的量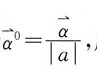 所以
所以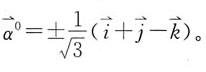
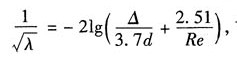 可以看出λ和雷诺数Re及管壁相对粗糙度Δ/d都有关.
可以看出λ和雷诺数Re及管壁相对粗糙度Δ/d都有关.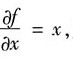 则
则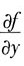 =______
=______
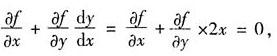 ,代入
,代入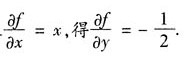
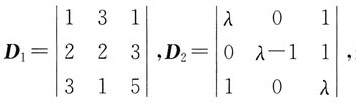 若D1=D2,则λ的值为______。
若D1=D2,则λ的值为______。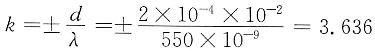 ,取整后可得最大级次为3。
,取整后可得最大级次为3。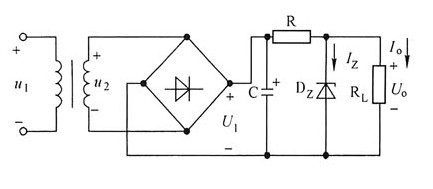
 确定了y是x的函数,且f'(t)存在,f(0)=2,f'(0)=2,则当t=0时,
确定了y是x的函数,且f'(t)存在,f(0)=2,f'(0)=2,则当t=0时,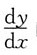 的值等于______。
的值等于______。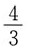
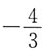
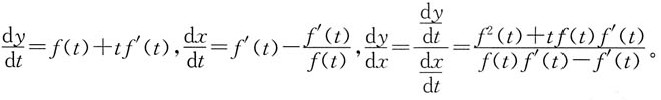
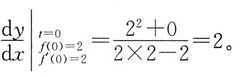
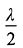
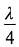
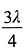
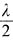 。
。
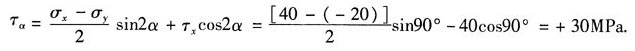
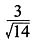
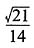
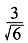
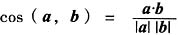 ,其中:a·b=axbx+ayby+azbz=3×1+(-1)×2+(-2)×(-1)=3,
,其中:a·b=axbx+ayby+azbz=3×1+(-1)×2+(-2)×(-1)=3,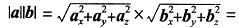
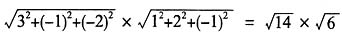 。因此,
。因此,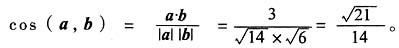
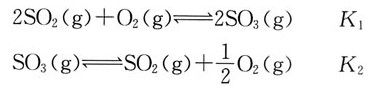
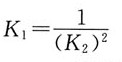
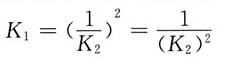
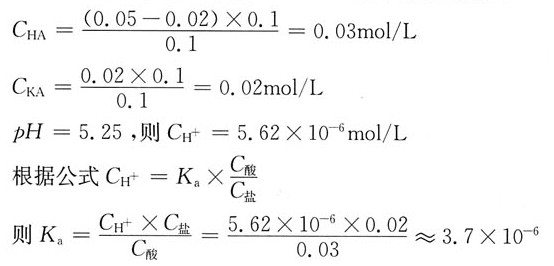
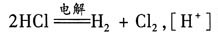 降低,pH增大;B项,H+得电子,OH-失电子,相当于电解
降低,pH增大;B项,H+得电子,OH-失电子,相当于电解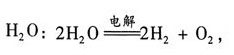 溶液的体积减小,[H+]升高,pH变小;C项,相当于电解H2O,pH不变;D项,相当于电解
溶液的体积减小,[H+]升高,pH变小;C项,相当于电解H2O,pH不变;D项,相当于电解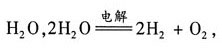 溶液的体积减小,
溶液的体积减小,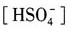 升高,[H+]升高,pH变小.
升高,[H+]升高,pH变小.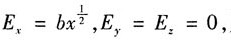 则立方体内的总电荷为______
则立方体内的总电荷为______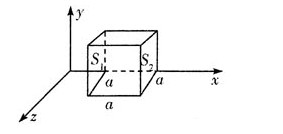
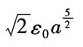
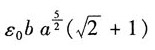
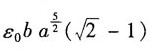
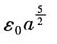
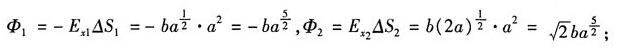 可得:
可得: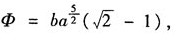 又知,
又知,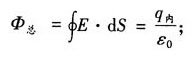 因此,得:
因此,得: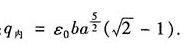
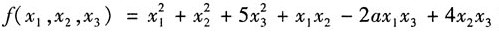 为正定的,则a的值为______
为正定的,则a的值为______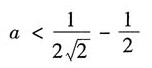
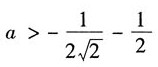
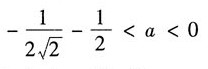
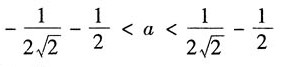
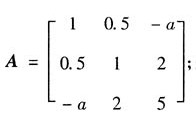 若二次型为正定的,则A的各阶主子式为正,因此,1>0;
若二次型为正定的,则A的各阶主子式为正,因此,1>0; 计算得:
计算得: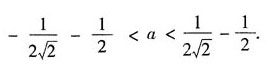
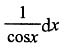
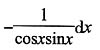
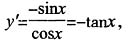 dy=-tanxdx。
dy=-tanxdx。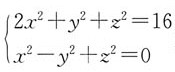 的柱面方程是______。
的柱面方程是______。