选择题(以下备选项中只有一项符合题目要求)7. 一元线性回归模型的总体回归直线可表示为______。
A.E(y
i)=α+βx
i B.
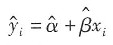
C.
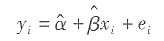
D.y
i=α+βx
i+μ
i A B C D
A
[解析] 对一元线性回归方程yi=α+βxi+μi两边同时求期望,则有E(yi)=α+βxi。表明点(xi,E(yi))在E(yi)=α+βxi对应的直线上,这条直线即为总体回归直线(或理论回归直线)。
8. 离散型随机变量的概率分布为
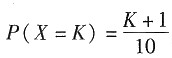
,K=0,1,2,3,则E(X)为______。
A B C D
C
[解析] 离散型随机变量期望值为
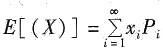
。根据
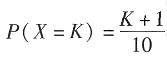
,得:
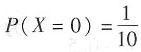
,
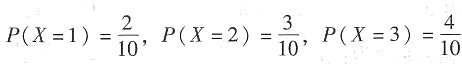
。所以,
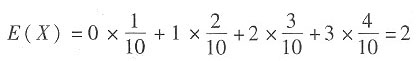
。
12. 设随机变量ζ的概率密度为
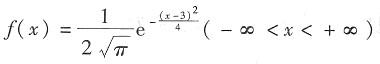
,则η=______~N(0, 1)。
A.
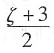
B.
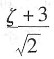
C.
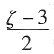
D.
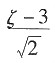
A B C D
D
[解析] 设X~N(μ,σ
2),则
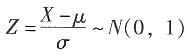
。由ζ的概率密度为
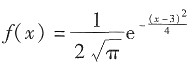
(-∞<x<+∞),可知:ζ的数学期望μ=3,方差σ
2=2,则
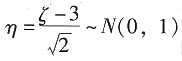
。
14. 从均值为200、标准差为50的总体中,抽出n=100的简单随机样本,用样本均值
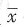
估计总体均值μ,则
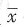
的期望值和标准差分别为______。
- A.200,5
- B.200,20
- C.200,0.5
- D.200,25
A B C D
A
[解析] 根据中心极限定理,设从均值为μ、方差为σ
2(有限)的任意一个总体中抽取样本量为n的样本,当n充分大时,样本均值
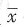
的抽样分布近似服从均值为μ,方差为σ
2/n的正态分布。由此可知
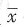
的期望值为μ=200,标准差为
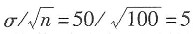
。
18. 以y表示实际观测值,
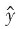
表示回归估计值,则普通最小二乘法估计参数的准则是使______最小。
A.
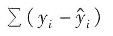
B.
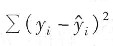
C.
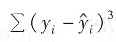
D.
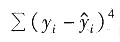
A B C D
B
[解析] 最小二乘准则认为,
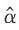
和
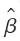
的选择应使得残差平方和最小,即:
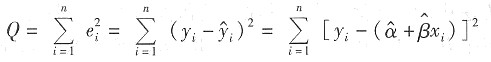
上式达到最小即为最小二乘准则(原理)。这种估计回归参数的方法称为普通最小二乘法(OLS)。
19. 回归模型Y
t=β
0+β
1X
t+μ
t中,检验H
0:β
1=0所用的统计量
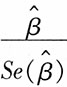
服从______。
- A.χ2(n-2)
- B.t(n-1)
- C.χ2(n-1)
- D.t(n-2)
A B C D
D
[解析] 一元线性回归模型中,用于检验回归系数β
1的统计量t为:

,该统计量服从自由度为n-2的t分布。
22. 样本判定系数R
2的计算公式是______。
A.
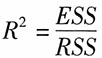
B.
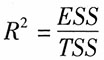
C.
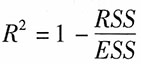
D.
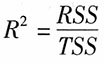
A B C D
B
[解析] 反映回归直线与样本观察值拟合程度的量是拟合优度,又称样本“可决系数”,常用R
2表示。其计算公式为:
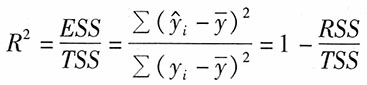
23. 对模型Y
i=β
0+β
1X
1i+β
2X
2i+μ
i的最小二乘回归结果显示,R
2为0.92,总离差平方和为500,则残差平方和RSS为______。
A B C D
B
[解析] 由
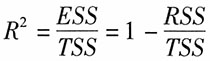
,即
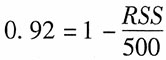
,解得:RSS=40。
27. 模型中,根据拟合优度R
2与F统计量的关系可知,当R
2=0时,有______。
A B C D
B
[解析] 拟合优度R
2为回归平方和(ESS)占总离差平方和(TSS)的比例,其计算公式为:
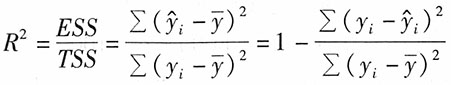
F统计量的计算公式为:
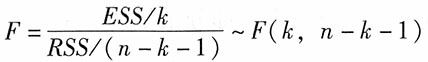
当R
2=0时,ESS=0,所以有F=0。
32. 假设对于某回归方程,计算机输出的部分结果如表所示。
| 回归方程输出结果 |
| | 系数 | 标准误(S.E.) | t-统计量值 | P-值 |
| 常数 | 2213.051 | 3291.366 | 0.672381 | 0.5075 |
| X变量 | 0.944410 | 0.066877 | 14.12166 | 0.0000 |
根据上表,下列说法错误的是______。
A.对应的t统计量为14.12166
B.
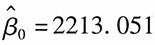
C.
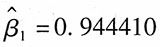
D.接受原假设H
0:β
1=0
A B C D
D
[解析] 由表可以看出,
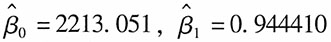
,β
1的标准误差为0.066877,对应的t统计量为14.12166。系数P值=0.0000,非常小,在这种情况下,当原假设为真时所得到的样本观察结果或更极端结果出现的概率很小,所以拒绝原假设。
40. 回归系数β
i在1-α的置信水平下的置信区间为______。
A.
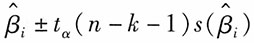
B.
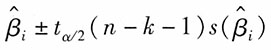
C.
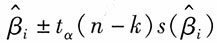
D.
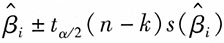
A B C D
B
[解析] 除了对回归系数进行检验外,还可以求出各回归系数的置信区间。一般回归系数β
i在1-α的置信水平下的置信区间为:
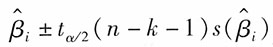
其中,
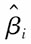
为回归系数估计值,n为样本数,k为自变量个数。
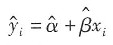
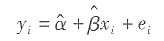
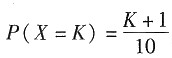 ,K=0,1,2,3,则E(X)为______。
,K=0,1,2,3,则E(X)为______。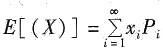 。根据
。根据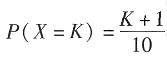 ,得:
,得: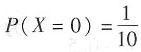 ,
,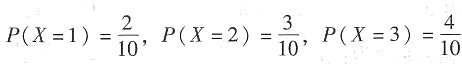 。所以,
。所以,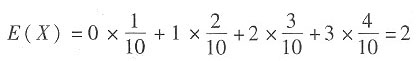 。
。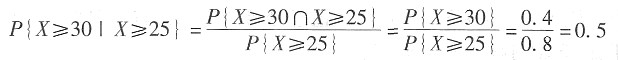
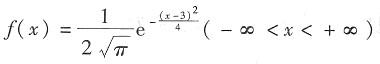 ,则η=______~N(0, 1)。
,则η=______~N(0, 1)。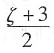
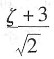
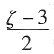
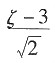
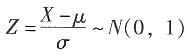 。由ζ的概率密度为
。由ζ的概率密度为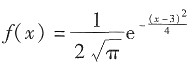 (-∞<x<+∞),可知:ζ的数学期望μ=3,方差σ2=2,则
(-∞<x<+∞),可知:ζ的数学期望μ=3,方差σ2=2,则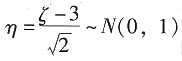 。
。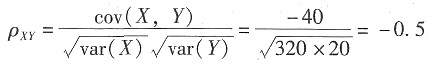 。
。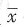 估计总体均值μ,则
估计总体均值μ,则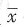 的期望值和标准差分别为______。
的期望值和标准差分别为______。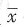 的抽样分布近似服从均值为μ,方差为σ2/n的正态分布。由此可知
的抽样分布近似服从均值为μ,方差为σ2/n的正态分布。由此可知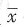 的期望值为μ=200,标准差为
的期望值为μ=200,标准差为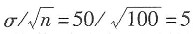 。
。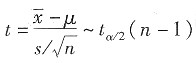 ,所以在显著性水平α下,接受域为|t|<tα/2(99)。
,所以在显著性水平α下,接受域为|t|<tα/2(99)。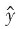 表示回归估计值,则普通最小二乘法估计参数的准则是使______最小。
表示回归估计值,则普通最小二乘法估计参数的准则是使______最小。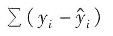
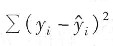
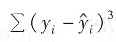
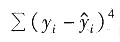
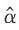 和
和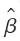 的选择应使得残差平方和最小,即:
的选择应使得残差平方和最小,即: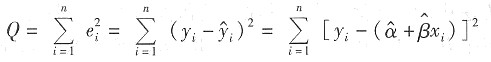
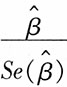 服从______。
服从______。 ,该统计量服从自由度为n-2的t分布。
,该统计量服从自由度为n-2的t分布。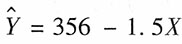 ,这说明______。
,这说明______。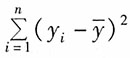
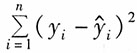
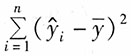

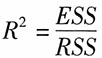
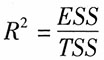
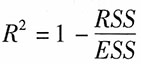
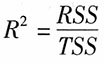
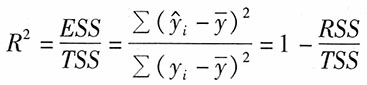
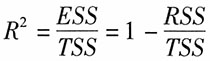 ,即
,即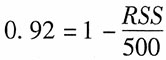 ,解得:RSS=40。
,解得:RSS=40。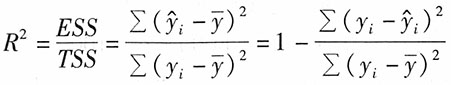
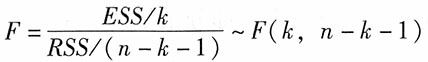
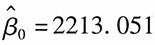
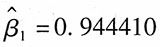
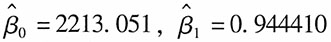 ,β1的标准误差为0.066877,对应的t统计量为14.12166。系数P值=0.0000,非常小,在这种情况下,当原假设为真时所得到的样本观察结果或更极端结果出现的概率很小,所以拒绝原假设。
,β1的标准误差为0.066877,对应的t统计量为14.12166。系数P值=0.0000,非常小,在这种情况下,当原假设为真时所得到的样本观察结果或更极端结果出现的概率很小,所以拒绝原假设。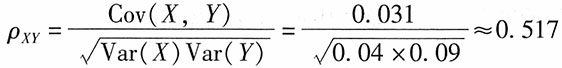 。当|r|≥0.8时,可视为高度相关;0.5≤|r|<0.8时,可视为中度相关;0.3≤|r|<0.5,视为低度相关;|r|<0.3时,说明两个变量之间的相关程度极弱,可视为不相关。因此,本题中X和Y为中度相关。
。当|r|≥0.8时,可视为高度相关;0.5≤|r|<0.8时,可视为中度相关;0.3≤|r|<0.5,视为低度相关;|r|<0.3时,说明两个变量之间的相关程度极弱,可视为不相关。因此,本题中X和Y为中度相关。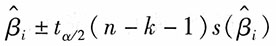 ,所以当临界值tα/2变大时,回归系数的置信区间将变大。
,所以当临界值tα/2变大时,回归系数的置信区间将变大。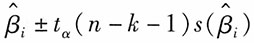
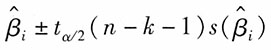
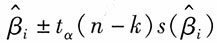
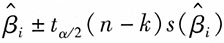
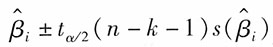
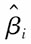 为回归系数估计值,n为样本数,k为自变量个数。
为回归系数估计值,n为样本数,k为自变量个数。