论述题1. 固溶体合金的相图如图所示,试根据相图确定:
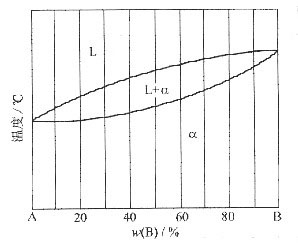
①成分为ω(B)=40%的合金首先凝固出来的固体成分;
②若首先凝固出来的固体成分含ω(B)=60%,合金的成分为多少?
③成分为ω(B)=70%的合金最后凝固的液体成分;
④合金成分为ω(B)=50%,凝固到某温度时液相含有ω(B)=40%,固体含有ω(B)=80%,此时液体和固体各占多少?
①在合金成分线与液相线相交点作水平线,此线与固相线交点的合金成分即为首先凝固出来的固体成分:ω(B)=85%。
②作ω(B)=60%垂直线与α固相线相交点的水平线,此线与液相线L相交点的成分即为合金成分:ω(B)=15%。
③原理同上:合金成分ω(B)=20%。
④利用杠杆定律:

固体所占的比例=1-75%=25%
2. 设冷变形后位错密度为10
12/cm
2的金属中,存在着加热时不发生聚集长大的第二相微粒,其体积分数φ=1%,半径为1μm,问这种第二相微粒的存在能否完全阻止此金属加热时再结晶(已知G=10
5MPa,b=0.3nm,比界面能σ=0.5J/m
2)。
再结晶驱动力
F=Gb
2(ρ-ρ
0)≈Gb
2ρ=10
11×(3×10
-10)
2×10
16=9×10
7N/m
2 再结晶阻力
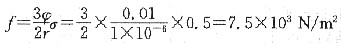
F>>f,故这种第二相微粒的存在不能完全阻止再结晶。
3. 为25℃时尺寸为25cm×25cm×3cm的长方体Al铸件设计型腔的尺寸(Al的线膨胀系数为25×10
-6/℃)。
为了最终得到特定尺寸的铸件,注入液态Al的型腔必须比铸件尺寸大。纯Al会在660℃始凝固,随着温度降低到室温,固态铸件尺寸会收缩。如果计算出了收缩量就可以得到型腔的最初尺寸。
Al的线膨胀系数为25×10-6/℃。从Al的凝固点到室温(25℃)的温度变化为660-25=635℃。尺寸变化可以由下式给出:
Al=l0-lf=αl0△T
对于25cm的尺寸,lf=25cm。求l0:
l0-25=(25×10-6)(l0)(635)
l0-25=0.015875l0
0.984l0=25
l0=25.40cm
对于3cm的尺寸,lf=3cm。求l0:
l0-3=(25×10-6)(l0)(635)
l0-3=0.015875l0
0.984l0=3
l0=3.05cm
所以,型腔尺寸应设计为25.40cm×25.40cm×3.05cm,这样铸件就会收缩到所需要的尺寸。
4. W在20℃时每10
23个晶胞中有一个空位,从20℃升温至1020℃时,点阵常数膨胀了(4×10
-4)%,而密度下降了0.012%,求W的空位形成能和形成熵。
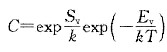
;而W的晶体结构为bcc,每个晶胞含有2个W原子,故
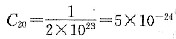
。由于升温时晶体总质量不变,即
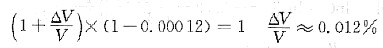
而晶体从T
1上升至T
2时,体积的膨胀是由点阵原子间距增大和空位浓度增高共同引起的,对边长为L的立方体,从T
1升至T
2时总的体积变化率
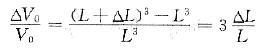
由点阵常数增大引起的体积变化率
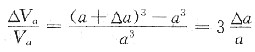
若T
1时空位浓度与T
2时相比可忽略不计,则T
2时的平衡空位浓度
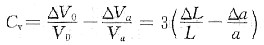
故C
1020=(0.012-3×4×10
-4)%=1×10
-4 因此,
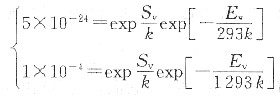
解得
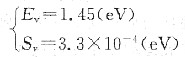
5. Co-Sb平衡相图如图所示。
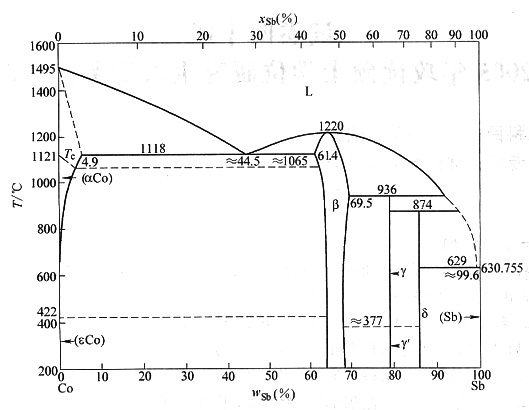
1.写出图中1118℃、≈1065℃、936℃、874C、629℃、422℃、≈377cC水平线的名称。
2.写出图中固态单相的相结构类型,并写出其中化合物的化学式。
3.写出w
Sb=90%的合金在200℃时的平衡相,并计算相组成物的相对量。
4.写出w
Sb=90%的合金在200℃时的平衡组织,并计算组织组成物的相对量。
1.1118℃:共晶反应线。
≈1065℃:磁性转变线。
936℃:包晶反应线。
8740℃:包晶反应线。
629℃:共晶反应线。
422℃:同素异构(多晶型)转变线。
≈377℃:有序一无序转变线。
2.(εCo)、(αCo)、(Sb)皆为置换固溶体。
β:CoSb。
γ和γ′:CoSb
2。
δ:CoSb
3。
3.平衡相:δ+(Sb),其中,
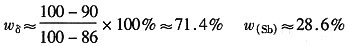
4.平衡组织:δ
先+(δ+(Sb))
共晶,其中
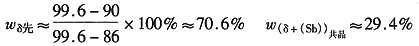
6. 解释冷变形金属加热时回复、再结晶的过程及特点。
冷变形金属加热时,各自特点如下:
(1) 回复过程的特征
①回复过程组织不发生变化,仍保持变形状态伸长的晶粒。
②回复过程使变形引起的宏观一类应力全部消除,微观二类应力大部分消除。
③回复过程中一般力学性能变化不大,硬度、强度仅稍有降低,塑性稍有提高,某些物理性能有较大变化,电阻率显著降低,密度增大。
④变形储能在回复阶段部分释放。
(2) 再结晶过程的特征
①组织发生变化,由冷变形的伸长晶粒变为新的等轴晶粒。
②力学性能发生急剧变化,强度、硬度急剧降低,塑性提高,恢复至变形前的状态。
③变形储能在再结晶过程中全部释放,三类应力(点阵畸变)清除,位错密度降低。
(3) 晶粒长大过程的特征
①晶粒长大。
②引起一些性能变化,如强度、塑性、韧性下降。
③伴随晶粒长大,还发生其他结构上的变化,如再结晶织构。
7. 含ω(Mn)为12.3%,ω(C)为1.34%的奥氏体钢,点阵常数为0.3624nm,密度为7.83g/cm
3,C,Fe,Mn的相对原子质量分别为12.01,55.85,54.94,试判断此固溶体的类型。
判断固溶体的类型,可以用该固溶体合金晶胞内的实际原子数(n)与纯溶剂晶胞内原子数的(n
0)的比值作为判据,有下式:

先计算该奥氏体钢的平均分子量:
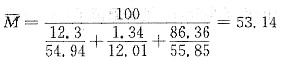
晶胞的体积
V=(0.3624×10
-7)
3=47.6×10
-24(cm
3)
故
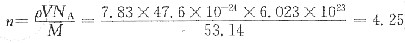
对于γ-Fe(奥氏体),n
0=4,故
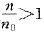
,即此同溶体必含有间隙原子。因为C原子半径比Fe,Mn原子半径小得多,故易处于间隙位置,形成C在Fe中的间隙固溶体。
设C处于Fe间隙位置形成的间隙固溶体的晶胞中平均原子数为n
1,由于固溶体中C的原子数分数
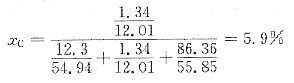
且
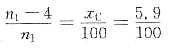
故可得n
1=4.25
由于

,所以Mn在合金中应为置换式固溶。
综上所述,可以判断此固溶体为C-间隙,Mn-置换式固溶体。
8. 形变
1.写出面心立方金属的一个具体的滑移系;多晶体变形时,在一定的形变量下,为何有的晶粒内是单系滑移而另一些晶粒内是多系滑移?为何有的晶粒内滑移量大而另一些晶粒内滑移量小?
2.什么是形变织构?有哪几类?如何表示?
1.如(111)
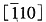
;这是形变的不均匀性;晶粒中某一滑移系相对于力轴的取向因子大时先滑移开动,取向因子小时后滑移开动,所以各晶粒的形变量不同;硬取向力轴引起多系滑移,如<111>、<100>、<110>方向,软取向力轴对应单系滑移,如<123>方向。
2.形变过程导致晶粒发生转动,最后各晶粒内的某些晶向趋于平行,这种因形变而导致取向择优称为形变织构。织构分为板织构和丝织构;板织构表示为{HKL}<UVW>,表示经轧制变形后,晶粒的{HKL}面转向平行于轧面,晶粒的<UVW>方向转到平行于轧向。丝织构表示为<UVW>。答轧制织构、拔丝织构也得分。