一、问题求解下列每题给出的A、B、C、D、E五个选项中,只有一项是符合试题要求的.1. 由21个不同的数组成的数集P,如果n∈P,且n是其他20个数的算术平均数的4倍,那么n与这21个数总和之比为
A.
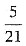
B.
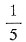
C.
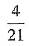
D.
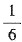
E.
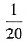
A B C D E
D
[考点] 实数的计算与比例的性质.
[解析] 由题意可得,n占其余20个数之和的
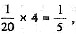
从而n占总和的
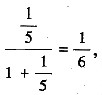
选D.
本题考查算术平均数的计算公式.
2. 已知方程ax
2+bx+c=0的两个根是-2和3,且函数y=ax
2+bx+c的最小值是
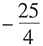
,则a,b,c分别为______.
- A.-1,1,6
- B.-2,2,3
- C.1,-1,-6
- D.2,-2,-3
- E.以上选项均不正确
A B C D E
C
[考点] 韦达定理,二次函数最值.
[解析] 思路一:将两根代入方程可得
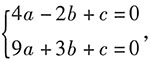
两式相减得a=-b.代入函数最小值表达式得

,a-4c=25.联立解得a=1,b=-1,c=-6.
思路二:方程ax
2+bx+c=0的两个根是-2和3,由二次方程的两根式可设方程为a(x-3)(x+2)=0,整理得ax
2-ax-6a=0.对比ax
2+bx+c=0可得a=-b,c=-6a.二次函数有最小值说明抛物线开口向上,a>0,故仅C选项符合.
10. 已知等差数列{a
n)中的第5项是
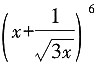
的常数项,则a
3+a
7=______
A.
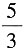
B.
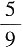
C.
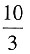
D.

E.5
A B C D E
C
[考点] 本题考查等差数列和二项式定理。
[解析] 根据二项式定理可得a
5=
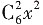
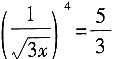
,由等差中项性质可得a
3+a
7=2a
5=
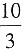
。故本题选C。
12. 若(x-a)
8=a
0+a
1x+a
2x
2+…+a
8x
8,且a
5=56,则a
0+a
1+a
2+…+a
8=______.
- A.0
- B.128
- C.256
- D.-256
- E.以上都不正确
A B C D E
C
[解析] (x-a)
8的展开式的通项公式为
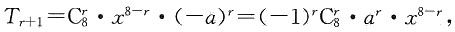
令8-r=5,则r=3,于是
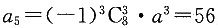
,解得a=-1,即(x+1)
8=a
0+a
1x+a
2x
2+…+a
8x
8,令x=1,则a
0+a
1+a
2+…+a
8=2
8=256.选C.
15. 大楼装有5个同类型的供水设备,如果每个供水设备使用情况是相互独立的,它们在任一时刻被使用的概率是0.1,则在同一时刻,至多有3个设备被使用的概率是
A.

B.
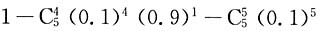
C.
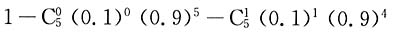
D.
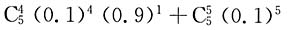
E.
A B C D E
B
[考点] 伯努利概型
[解析] 至多有3个设备被使用,考虑反面,至少有4个设备被使用的概率为
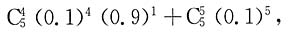
因此概率
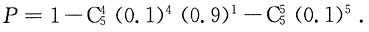
选B.
三、逻辑推理下列每题给出的A、B、C、D、E五个选项中,只有一项是符合试题要求的。 钱有光中毒死亡。嫌疑人赵晨和孙广受到法官李广的审讯。赵晨说:“如果钱有光是被谋杀,那肯定是孙广作的案。”孙广说:“如果钱有光不是被谋杀,那就是自杀。”对此,法官李广做出了如下的假定:
(1)如果赵晨和孙广都没有撒谎,那么钱有光中毒死亡就是一次意外事故;
(2)如果赵晨和孙广两人中有一人撒谎,那么钱有光中毒死亡就不是一次意外事故。 1. 论证有效性分析:分析下述论证中存在的缺陷和漏洞,写一篇600字左右的文章,对该论证的有效性进行分析和评论。
下面是奥林匹克食品公司(加工冷冻食品)呈送给公司股东的年度报告的一部分:
在此期间,加工的成本下降了,因为企业已经学会了更加有效的工作。例如,在彩色胶卷的加工上,3寸~5寸的彩色照片从1970年的50美分(5天取货)下降到1984年的20美分(1天取货)。同样的道理适用于食品的加工上。因为奥林匹克食品公司不久将要庆祝它成立25周年,由此我们认为我们的长期的经验将使我们能做到成本最小化和利润最大化。
论证有效性分析参考范文
通过引用彩色胶卷加工业在14年间胶卷加工成本下降趋势的事例,作者认为奥林匹克食品公司将来也能使成本最小化和使利润最大化。为了支持这个结论,作者引用了具有普遍意义的原理“因为企业懂得了如何将事情做得更好,所以它们的效率将更高”。这个原理与奥林匹克食品公司在业内25年的食品加工经验一道,使作者产生了“粉红色的预期”。题干的论证是没有说服力的。因为作者犯了两个致命的错误:
第一,作者的“成本最小化和利润最大化”的预期是基于毫无理由的假设:奥林匹克食品公司的“长期的经验”已经使奥林匹克食品公司懂得了如何将事情做得更好,但是并不能保证事实真的就是如此。很有可能奥林匹克食品公司在25年里并未学到食品加工的任何经验,缺乏这种假设,提高效率的预期就完全不能成立。
第二,彩色胶卷加工业的事例能应用于食品加工行业是很值得怀疑的。这两个行业的区别远远大于其相似的地方,所以将两者进行类比是无效的。例如,食品损坏问题、污染问题以及及时的运送等问题都将可能影响食品业的发展,但是这些影响因素在胶卷加工行业却几乎是不存在的。这些问题将有可能造成不可克服的困难,阻止食品行业在未来降低食品加工的成本。
正如题干的论述,作者的论证并未说明其结果的必然性。要想加强奥林匹克食品公司能在未来“做到成本最小化和利润最大化”这样的结论,作者必须提供足够的证据来表明奥林匹克食品公司通过25年的行业经验已经学会了如何将事情办得更好。与食品加工行业更加相似的支持性实例将进一步证实作者的观点。
1.
论说文:根据下述材料,写一篇700字左右的论说文,题目自拟。 我国著名的医学专家钟南山为我国的医学事业做出了不朽的贡献,他在大学期间成绩体育突出,曾经打破过第一届全运会的400米栏全国纪录,但是他分析自己的身体素质认为学医能够创造更大的贡献,便放弃运动员的生涯选择了深入医学研究,经过几十年刻苦的努力,最终成为了我国医学史上的不朽传奇。这或许能够对纠结“选择重要”还是“努力重要”的人一部分启示。
[范文]
所有的成功都是选择与努力的结合
钟南山院士虽然曾经获得过优秀的体育成绩,但是他综合分析了自身的优势,毅然选择了医学,并且在选择之后艰苦奋斗几十年,最后为中华民族立下了不朽的功勋。他的事例给了我们到底是选择重要还是努力重要的深刻启示:所有的成功都是选择与努力的结合。
没有正确的选择,努力换来的可能是事倍功半的结果。齐人有言:“虽有智慧,不如乘势。”正确的选择就是一种乘势,当我们的选择正确,事物的发展规律、环境带来的影响等等都会顺应我们的选择,我们只需要按照正确的发展方向努力即可。如果没有正确的选择而只是埋头努力,那么就如同只是低头拉车从不抬头看路,前路尽是蜿蜒曲折、残垣断壁,甚至最后落得一个南辕北辙的效果,看似十分努力,最后却与成功背道而驰。
没有后续的努力,正确的选择只能带来稍纵即逝的光明。运气、环境、时势、思维方式等都可以让选择正确,但是仅仅选择正确不代表我们就迎来了成功,要将正确选择带来的成果落地才是选择真正的成功。而所有成果的落地都少不了努力,无论是个人事务、企业决策、国家方针,都无一例外需要不断地努力。正如我们当年选择了改革开放这条康庄大道,但是选择不代表就能立刻实现,一代代人的艰苦奋斗,寒来暑往四十个春秋,才让我们走上这条康庄大道,即便如此,在取得成就之后依旧不能停下奋斗的脚步,依旧要保持“征途漫漫,唯有奋斗”的笃行精神,这样才能让正确的选择落地成为真正的成功!
如何才能将正确的选择和不懈的努力紧密地结合?首先是辨别正确的选择,正确的选择永远是符合道义的,永远是符合造福更多人利益的选择,而并非为了一己私欲的狭义选择。其次是深刻认识到即便是选择正确也需要一颗谦卑之心不断去努力,不能仅仅因为选择正确就开始骄傲自大,忘记了需要将成果落地的道理。最后就只能落得秋风扫落叶连选择带来的一点点好处也遗失殆尽了。
不选择瞎努力无法带来成功,只选择不努力也无法将选择带来的好处落地。我们必须要将正确的选择和不懈的努力结合起来,这样才能既选择正确又能将选择落地成功。
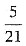
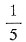
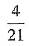
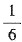
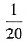
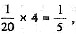 从而n占总和的
从而n占总和的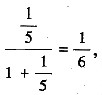 选D.
选D.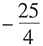 ,则a,b,c分别为______.
,则a,b,c分别为______.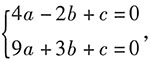 两式相减得a=-b.代入函数最小值表达式得
两式相减得a=-b.代入函数最小值表达式得 ,a-4c=25.联立解得a=1,b=-1,c=-6.
,a-4c=25.联立解得a=1,b=-1,c=-6.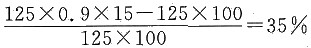 。
。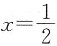 ,且f(0)=a>0.由二次函数的对称性可知f(1)=f(0)=a>0.因为抛物线的开口向上,所以由图象可知当x>1时,恒有f(x)>0.又f(m)<0,0<m<1,而m+1>1,故f(m+1)>0.选A.
,且f(0)=a>0.由二次函数的对称性可知f(1)=f(0)=a>0.因为抛物线的开口向上,所以由图象可知当x>1时,恒有f(x)>0.又f(m)<0,0<m<1,而m+1>1,故f(m+1)>0.选A.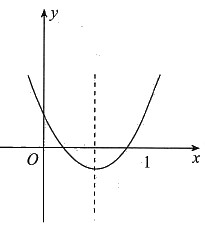
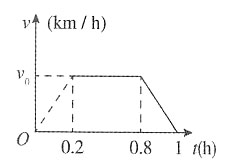
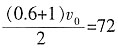 ,解得v0=90。故本题选C。
,解得v0=90。故本题选C。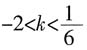
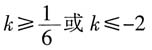
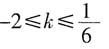
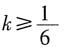
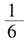 ,代入B点解k值为-2。A、B两点分别在第四、第二象限,且直线必过点(0,4)。当
,代入B点解k值为-2。A、B两点分别在第四、第二象限,且直线必过点(0,4)。当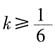 或k≤-2时,直线y=kx+4与线段AB恒有交点。故选C。
或k≤-2时,直线y=kx+4与线段AB恒有交点。故选C。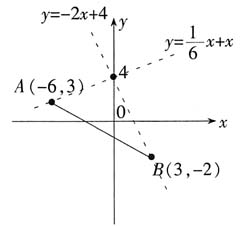
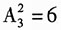 种.(2)用一位全能歌舞演员和一个其他歌舞演员,则有安排方案
种.(2)用一位全能歌舞演员和一个其他歌舞演员,则有安排方案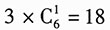 种.(3)不用全能歌舞演员,则有安排方案4×2=8种.则共有安排方式32种.
种.(3)不用全能歌舞演员,则有安排方案4×2=8种.则共有安排方式32种.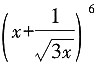 的常数项,则a3+a7=______
的常数项,则a3+a7=______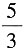
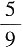
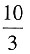

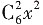
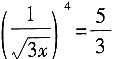 ,由等差中项性质可得a3+a7=2a5=
,由等差中项性质可得a3+a7=2a5=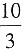 。故本题选C。
。故本题选C。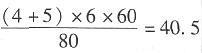 ,因此两人游了40个来回,之后又游了40米,因此相遇41次。
,因此两人游了40个来回,之后又游了40米,因此相遇41次。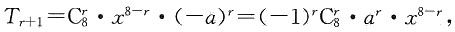
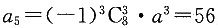 ,解得a=-1,即(x+1)8=a0+a1x+a2x2+…+a8x8,令x=1,则a0+a1+a2+…+a8=28=256.选C.
,解得a=-1,即(x+1)8=a0+a1x+a2x2+…+a8x8,令x=1,则a0+a1+a2+…+a8=28=256.选C.
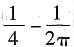
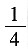
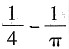
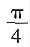
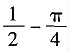
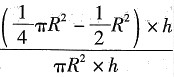 ,解得
,解得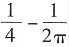 。
。
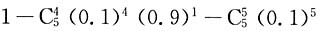
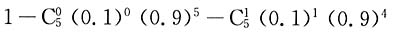
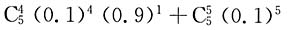
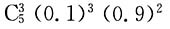
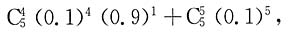 因此概率
因此概率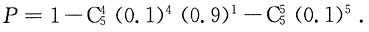 选B.
选B.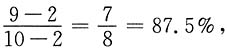 充分;
充分;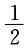 千克,2小时蒸发1千克,剩余为
千克,2小时蒸发1千克,剩余为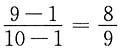 ,不充分.选A.
,不充分.选A.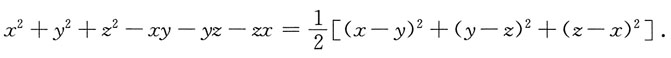
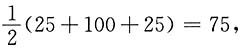 充分;
充分;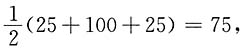 充分.选D.
充分.选D.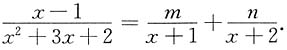
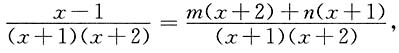 即
即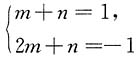 时,即
时,即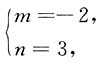 等式成立,所以条件(1)不充分,条件(2)充分.选B.
等式成立,所以条件(1)不充分,条件(2)充分.选B.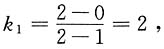 直线BC斜率
直线BC斜率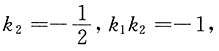 所以AC和BC直线垂直,充分.选D.
所以AC和BC直线垂直,充分.选D.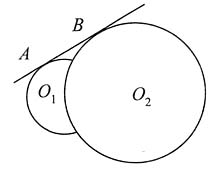
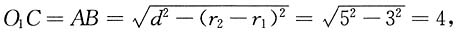 充分.选C.
充分.选C. 条件(1)不充分,条件(2)不充分,根据勾股定理,距离都存在超过10的坐标范围,联合不充分.选E.
条件(1)不充分,条件(2)不充分,根据勾股定理,距离都存在超过10的坐标范围,联合不充分.选E.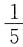 .
.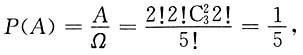 充分;
充分;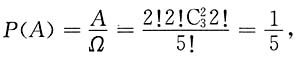 充分.选D.
充分.选D.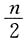 间,还剩
间,还剩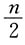 间房和20人,其中20人中每8人一间,则有2间房住满,还剩4人,又因为每间8人,仅有一间未满,则可知
间房和20人,其中20人中每8人一间,则有2间房住满,还剩4人,又因为每间8人,仅有一间未满,则可知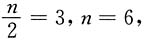 充分.选C.
充分.选C.