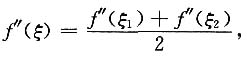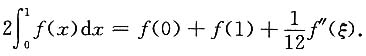一、选择题1. 二次型
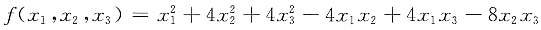
的规范形是______
A.
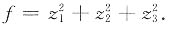
B.
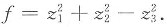
C.
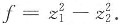
D.

A B C D
D
[解析] 思路一:二次型的规范形由它的正负惯性指数确定
二次型的矩阵
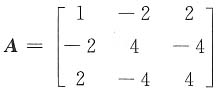
,其特征多项式为
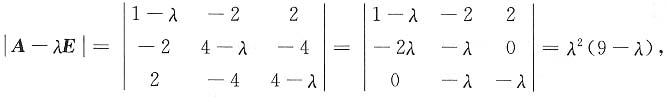
故A的特征值为9,0,0,正惯性指数p=1,负惯性指数q=0,则f的规范形为
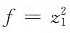
.
思路二:配方法
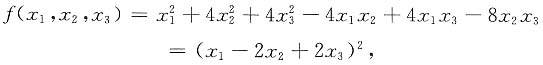
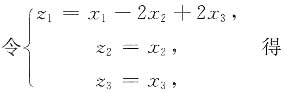
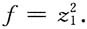
2. 已知
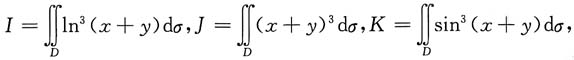
其中D由x=0,y=0,x+y=1围成,则______
- A.I<J<K.
- B.K<J<I.
- C.I<K<J.
- D.K<I<J.
A B C D
C
[解析] 由于积分区域相同,可通过比较函数值的大小来求解.
因为在积分区域D内,0≤x+y≤1,则有
ln(x+y)≤sin(x+y)≤x+y
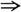
ln
3(x+y)≤sin
3(x+y)≤(x+y)
3,
故
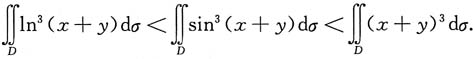
3. 当x→0时,下列3个无穷小
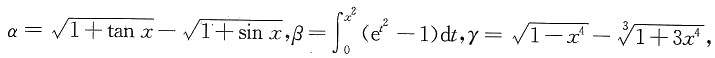
按后一个无穷小比前一个高阶的次序排列,正确的次序是______
- A.α,β,γ.
- B.γ,β,α.
- C.γ,α,β.
- D.α,γ,β.
A B C D
D
[解析]
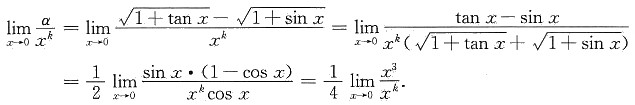
所以当x→0时,
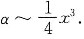
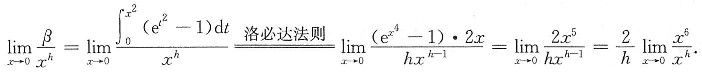
所以当x→0时,
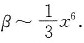
对于γ,用带有佩亚诺余项的泰勒展开式展开最方便.

所以当x→0时,
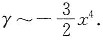
综合之,从低到高排列应是α,γ,β.选D.
4. 下列命题中正确的是______
A.设正项级数
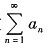
发散,则
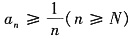
B.设级数
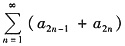
收敛,则级数
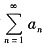
收敛
C.设
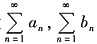
至少有一个发散,则
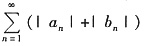
发散
D.设
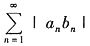
收敛,则
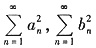
都收敛
A B C D
C
[考点] 数项级数的收敛与发散
[解析] A不正确. 令
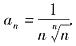
当n>1时,
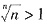
,则

由
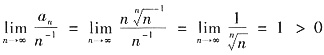
,依正项级数比较法极限形式知
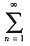
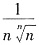
发散.
B不正确,反例:
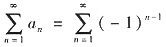
发散. 但
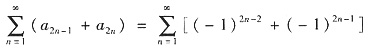
=(-1)
n-1(1-1)+(1+1)+…+(1-1)+…是收敛的.
C正确,反证:设不然,
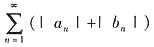
收敛,则由|a
n|≤|a
n|+|b
n|;|b
n|≤|a
n|+|b
n|知
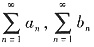
都绝对收敛,与已知其中至少有一个发散矛盾.
D不正确,反例
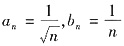
,则
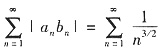
收敛,而
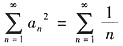
发散,故选C.
6. 设3维向量α
1,α
2,α
3线性相关,α
2,α
3,α
4线性无关,记(β
1,β
2,β
3)=(α
1,α
2,α
3)A,(γ
1,γ
2,γ
3)=(α
2,α
3,α
4)B,则下列正确的是______.
- A.存在矩阵A,使得β1,β2,β3线性无关
- B.不存在矩阵A,使得β1,β2,β3线性相关
- C.存在矩阵B,使得γ1,γ2,γ3线性无关
- D.不存在矩阵B,使得γ1,γ2,γ3线性相关
A B C D
C
[考点] 向量的线性关系.
[解析] 利用向量的线性关系的性质求解.
因为3维向量α2,α3,α4线性无关,所以任何3维向量都可由α2,α3,α4线性表示.所以存在矩阵B,使得(γ1,γ2,γ3)=(α2,α3,α4)B. 故选C.
本题用到结论:如果向量组中向量的个数大于向量的维数,则向量一定线性相关.
7. 设幂级数
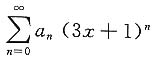
在x=-1处收敛,则级数
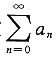
______.
- A.绝对收敛
- B.条件收敛
- C.发散
- D.敛散性不能确定
A B C D
A
[解析] 令3x+1=t,则级数
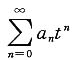
当t=-2时收敛,故级数
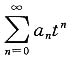
的收敛半径R≥2,
因为1<R,所以当t=1时,级数
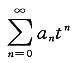
绝对收敛,即级数
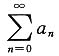
绝对收敛,应选A.
8. 设函数z=z(x,y)由方程
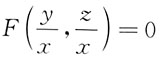
确定,其中F为可微函数,且
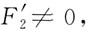
则
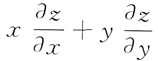
=______.
A B C D
B
[考点] 多元复合函数的求导法则,多元隐函数的求导法则.
[解析] 本题可通过多元隐函数的求导公式计算.
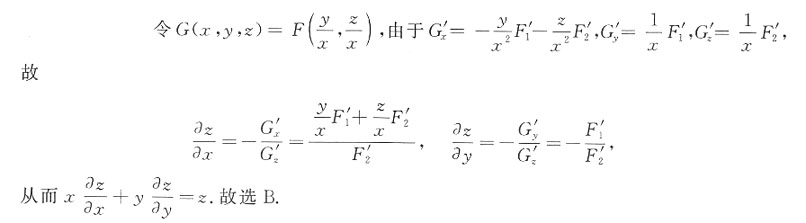
多元抽象隐函数的求导往往涉及多元复合函数的求导法则的使用.
9. 下列四个命题:
(1)若f(x)在x=x
0处可导,则|f(x)|在x=x
0处可导.
(2)若|f(x)|在x=x
0处可导,则f(x)在x=x
0处可导.
(3)若f(x)在x=x
0处可导,且f(x
0)=0,f'(x
0)≠0,则|f(x)|在x=x
0处不可导.
(4)若f(x)在x=x
0处连续,且|f(x)|在x=x
0处可导,则f(x)在x=x
0处可导.
正确的命题个数是______.
A B C D
C
[考点] 导数的定义.
[解析] 利用反例并结合单侧导数的定义.
对于命题(1),设f(x)=x,x
0=0,显然f(x)在x
0=0处可导,但是|f(x)|=|x|在x
0=0处不可导,命题错误.
对于命题(2),设
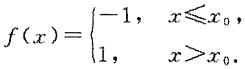
显然f(x)在x=x
0处不连续、不可导,但是|f(x)|=1在x=x
0处可导,命题错误.
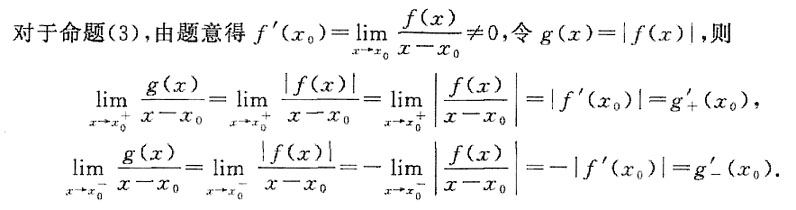
又因为
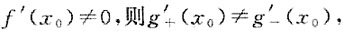
所以g(x)在x=x
0处不可导,命题正确.
对于命题(4),若f(x
0)≠0,不妨令f(x
0)>0,又f(x)在x=x
0处连续,则
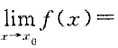
f(x
0)>0,由函数极限的局部保号性知,存在x
0的某邻域,使得f(x)>0,从而g(x)=|f(x)|=f(x).由g(x)=|f(x)|在x=x
0处可导知,f(x)在x=x
0处可导.对于f(x
0)<0可类似说明.若f(x
0)=0,则由g(x)=|f(x)|在x=x
0处可导知,
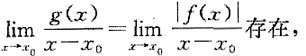
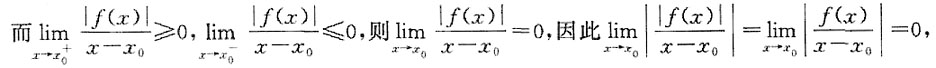
即f(x)在x=x
0处可导,命题正确.
故应选C.
二、填空题1. 设z=(x+e
y)
x,则
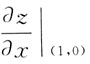
=______.
2ln2+1
[考点] 求二元幂指函数的偏导数.
[解析] 本题应先对函数取对数,再求偏导数.
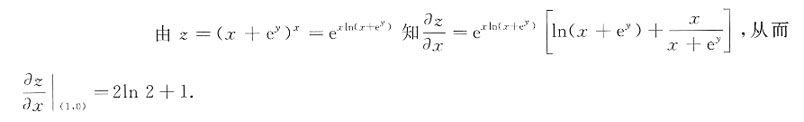
求二元幂指函数的偏导数是考生的薄弱环节,应引起重视.
2. 设曲面S由方程
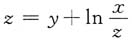
确定,则S在点M
0(1,1,1)处的法线所在直线的参数式方程为______.
[解析] 因点M
0(1,1,1)满足方程z=y+lnx-lnz,即点M
0在曲面S上.又
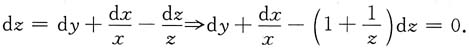
因此在在曲面S上点(x,y,z)处的法向量为
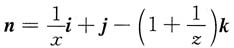
,在M
0(1,1,1)点处的法向量为n
M0=i+j-2k.
故S在点M
0(1,1,1)处的法线的直线的参数式方程为
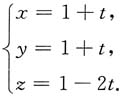
3. 设函数y=y(x)由方程ln(x
2+y)=x
2+sinx确定,则
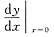
=______.
4. 设X~B
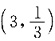
,Y服从[0,3]上的均匀分布,且X与Y独立,则行列式
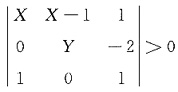
的概率为______.
[解析]
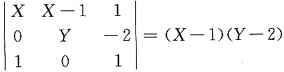
,于是所求概率为
p=P{(X-1)(Y-2)>0}
=P(X-1>0,Y-2>0}+P(X-1<0,Y-2<0}
=P{X>1}P{Y>2}+P{X<1}P{Y<2}
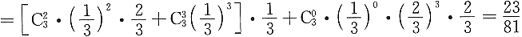
5. 幂级数
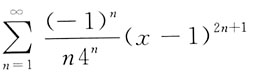
的收敛域为______.
[-1,3]
[考点] 幂级数的收敛域.
[解析] 本题可通过换元来求收敛域.
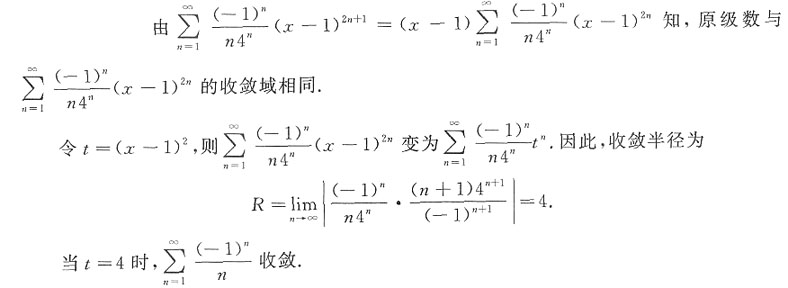
由(x-1)
2≤4得-1≤x≤3,故原级数的收敛域为[-1,3].
在求幂级数的收敛域时,注意讨论端点处的收敛性.
6. 二次型f(x
1,x
2,…,x
n)=(nx
1)
2+(nx
2)
2+…+(nx
n)
2-(x
1+x
2+…+x
n)
2的秩为______.
n
[考点] 二次型的秩.
[解析] 写出二次型的矩阵,求矩阵的秩,即为二次型的秩.
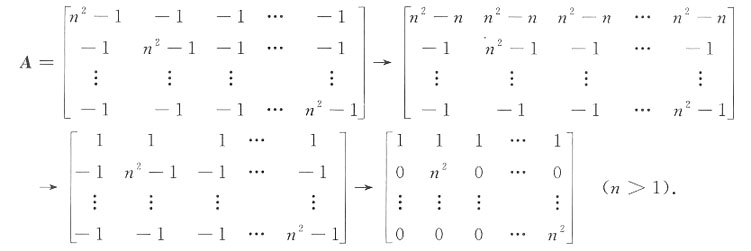
可见二次型f的秩为n.
再一次强调,矩阵秩的考查相对会比较综合.本题即为秩与二次型的结合.
三、解答题(70分)2. 设f(x)在[0,2]上连续,在(0,2)内三阶可导,且
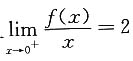
,f(1)=1,f(2)=6.证明:存在ξ∈(0,2),使得f'''(ξ)=9.
解:由
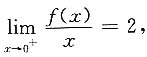
得f(0)=0,f'(0)=2.
作多项式P(x)=Ax
3+Bx
2+Cx+D,使得P(0)=0,P'(0)=2,P(1)=1,P(2)=6,
解得
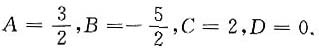
令
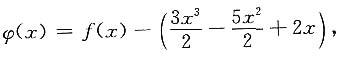
则φ(x)在[0,2]上连续,在(0,2)内可导,且φ(0)=φ(1)=φ(2)=0,因此φ(x)在[0,1]和[1,2]上都满足罗尔定理的条件,则存在ξ
1∈(0,1),ξ
2∈(1,2),使得φ'(ξ
1)=φ'(ξ
2)=0.
又φ'(0)=0,由罗尔定理,存在η
1∈(0,ξ
1),η
2∈(ξ
1,ξ
2),使得φ''(η
1)=φ''(η
2)=0,再由罗尔定理,存在ξ∈(η
1,η
2)
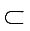
(0,2),使得φ''(ξ)=0.而φ'''(x)=f'''(x)-9,所以f'''(ξ)=9.
3. 设随机变量X
1,X
2,…,X
n相互独立且在[0,a]上服从均匀分布,令U=max{X
1,X
2,…,X
n},求U的数学期望与方差.
解:F
U(u)=P(U≤u)=P{max(X
1,X
2,…,X
n)≤u}=P{X
1≤u,X
2≤u,…,X
n≤u}
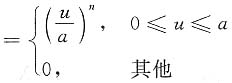
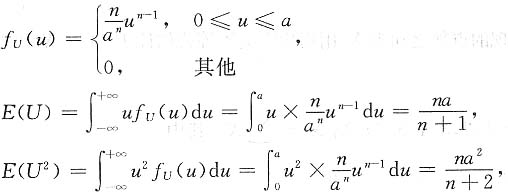
于是
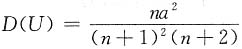
.
4. 求
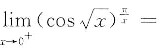
______.
解:此函数属1
∞型.
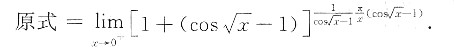
由于
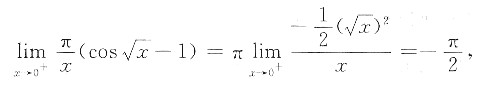
故 原式=e
-x/2.
[解析] 求函数的极限.
 令随机变量
令随机变量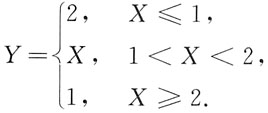 求:
求:5. Y的分布函数;
解:设Y的分布函数为F(y),则
F(y)=P{Y≤y}.
当y<1时,F(y)=0;
当1≤y<2时,
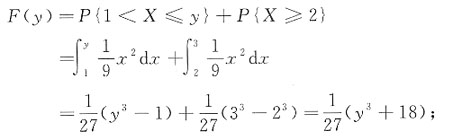
当y≥2时,
F(y)=1.
[考点] 随机变量的分布函数及概率.
[解析] (1)直接利用分布函数的定义求分布函数;
(2)利用X的概率密度求概率.
用定义法求随机变量的分布函数以及用概率密度求概率均为考研中的基本题型.
6. 概率P{X≤Y}.
解:
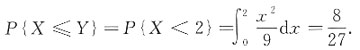
[考点] 随机变量的分布函数及概率.
7. 设f(x)在[0,1]上二阶连续可导,且f'(0)=f'(1).证明:存在ξ∈(0,1),使得
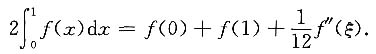
证:令
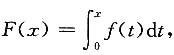
则F(x)三阶连续可导且F'(x)=f(x),由泰勒公式得
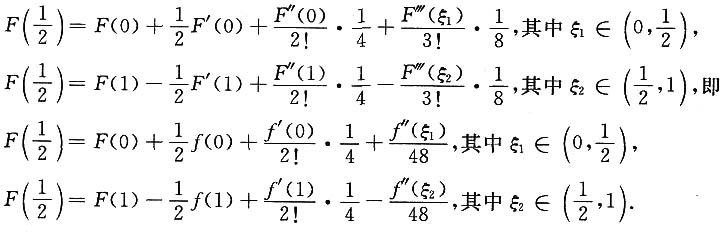
两式相减得
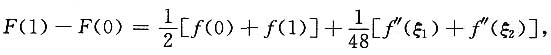
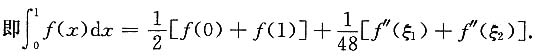
因为f''(x)∈C[ξ
1,ξ
2],所以f''(x)在[ξ
1,ξ
2]上取到最大值M和最小值m,
于是2m≤f''(ξ
1)+f''(ξ
2)≤2M或
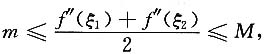
由介值定理,存在ξ∈[ξ
1,ξ
2]
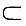
(0,1),使得
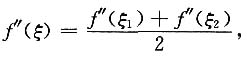
故有
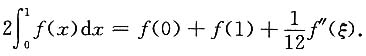
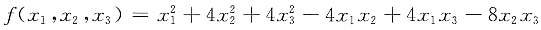 的规范形是______
的规范形是______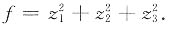
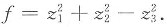
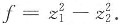

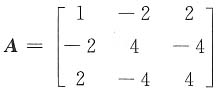 ,其特征多项式为
,其特征多项式为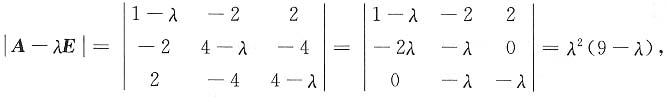
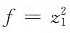 .
.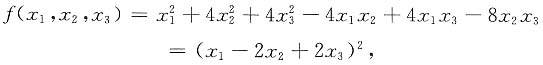
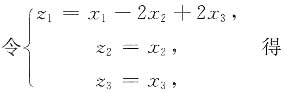
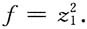
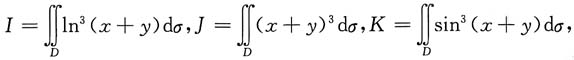
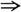 ln3(x+y)≤sin3(x+y)≤(x+y)3,
ln3(x+y)≤sin3(x+y)≤(x+y)3,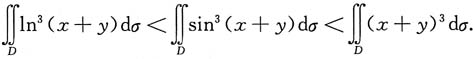
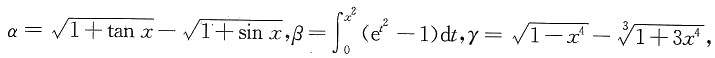
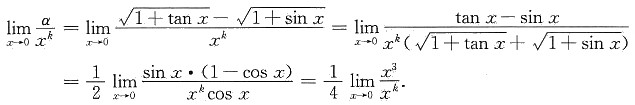
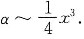
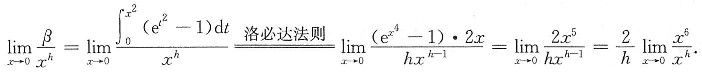
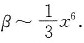

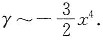 综合之,从低到高排列应是α,γ,β.选D.
综合之,从低到高排列应是α,γ,β.选D.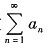 发散,则
发散,则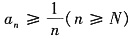
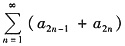 收敛,则级数
收敛,则级数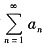 收敛
收敛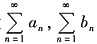 至少有一个发散,则
至少有一个发散,则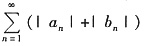 发散
发散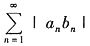 收敛,则
收敛,则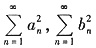 都收敛
都收敛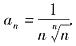 当n>1时,
当n>1时,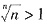 ,则
,则
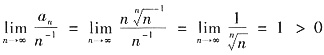 ,依正项级数比较法极限形式知
,依正项级数比较法极限形式知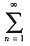
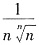 发散.
发散.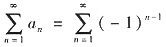 发散. 但
发散. 但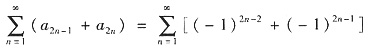
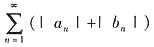 收敛,则由|an|≤|an|+|bn|;|bn|≤|an|+|bn|知
收敛,则由|an|≤|an|+|bn|;|bn|≤|an|+|bn|知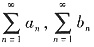 都绝对收敛,与已知其中至少有一个发散矛盾.
都绝对收敛,与已知其中至少有一个发散矛盾.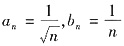 ,则
,则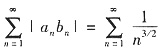 收敛,而
收敛,而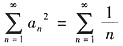 发散,故选C.
发散,故选C.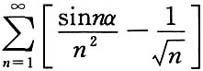
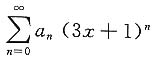 在x=-1处收敛,则级数
在x=-1处收敛,则级数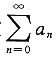 ______.
______.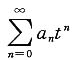 当t=-2时收敛,故级数
当t=-2时收敛,故级数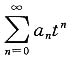 的收敛半径R≥2,
的收敛半径R≥2,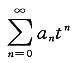 绝对收敛,即级数
绝对收敛,即级数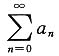 绝对收敛,应选A.
绝对收敛,应选A.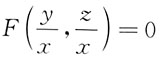 确定,其中F为可微函数,且
确定,其中F为可微函数,且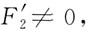 则
则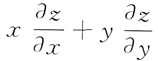 =______.
=______.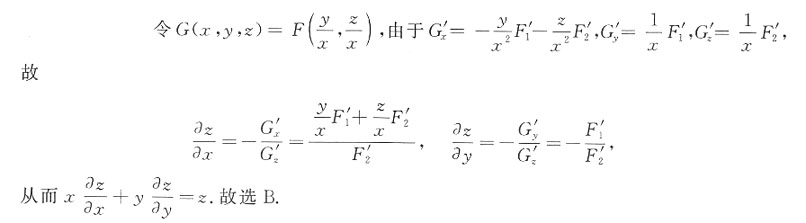
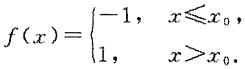 显然f(x)在x=x0处不连续、不可导,但是|f(x)|=1在x=x0处可导,命题错误.
显然f(x)在x=x0处不连续、不可导,但是|f(x)|=1在x=x0处可导,命题错误.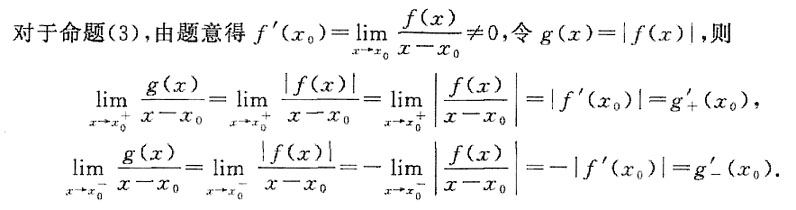
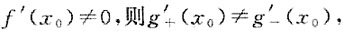 所以g(x)在x=x0处不可导,命题正确.
所以g(x)在x=x0处不可导,命题正确.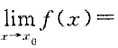 f(x0)>0,由函数极限的局部保号性知,存在x0的某邻域,使得f(x)>0,从而g(x)=|f(x)|=f(x).由g(x)=|f(x)|在x=x0处可导知,f(x)在x=x0处可导.对于f(x0)<0可类似说明.若f(x0)=0,则由g(x)=|f(x)|在x=x0处可导知,
f(x0)>0,由函数极限的局部保号性知,存在x0的某邻域,使得f(x)>0,从而g(x)=|f(x)|=f(x).由g(x)=|f(x)|在x=x0处可导知,f(x)在x=x0处可导.对于f(x0)<0可类似说明.若f(x0)=0,则由g(x)=|f(x)|在x=x0处可导知,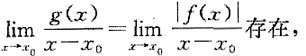
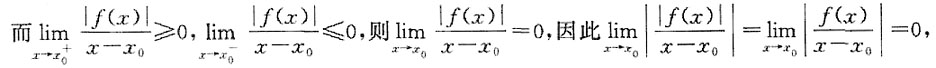 即f(x)在x=x0处可导,命题正确.
即f(x)在x=x0处可导,命题正确.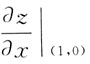 =______.
=______.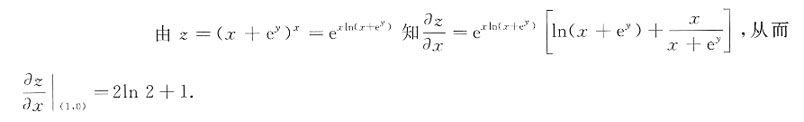
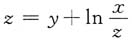 确定,则S在点M0(1,1,1)处的法线所在直线的参数式方程为______.
确定,则S在点M0(1,1,1)处的法线所在直线的参数式方程为______.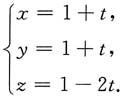
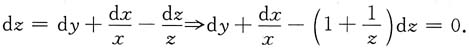
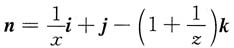 ,在M0(1,1,1)点处的法向量为nM0=i+j-2k.
,在M0(1,1,1)点处的法向量为nM0=i+j-2k.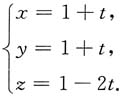
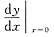 =______.
=______.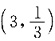 ,Y服从[0,3]上的均匀分布,且X与Y独立,则行列式
,Y服从[0,3]上的均匀分布,且X与Y独立,则行列式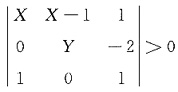 的概率为______.
的概率为______.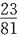
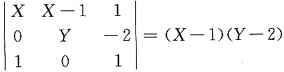 ,于是所求概率为
,于是所求概率为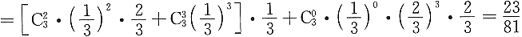
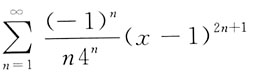 的收敛域为______.
的收敛域为______.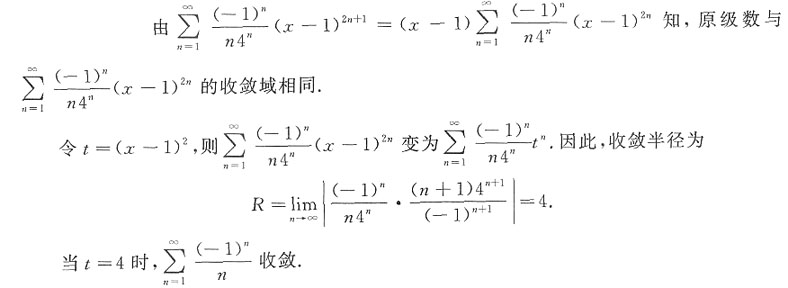

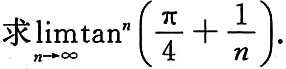
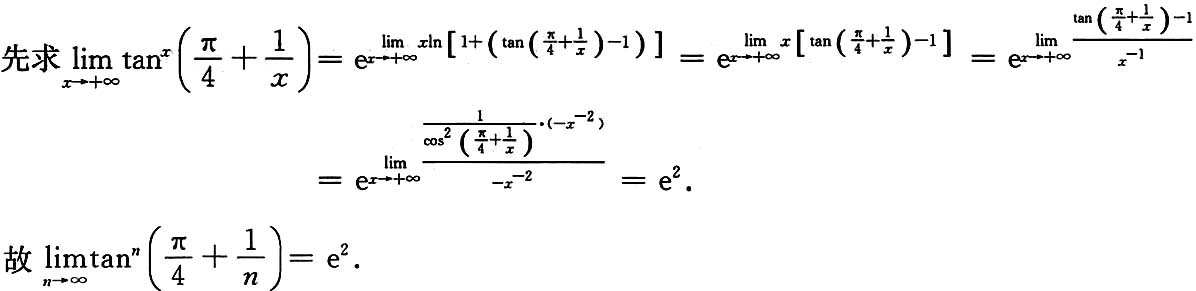
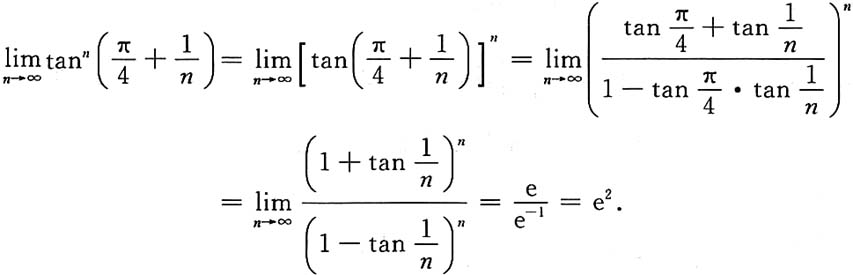
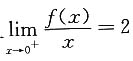 ,f(1)=1,f(2)=6.证明:存在ξ∈(0,2),使得f'''(ξ)=9.
,f(1)=1,f(2)=6.证明:存在ξ∈(0,2),使得f'''(ξ)=9.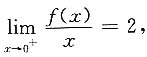 得f(0)=0,f'(0)=2.
得f(0)=0,f'(0)=2.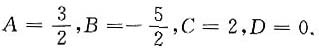
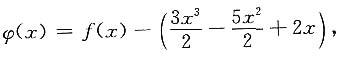 则φ(x)在[0,2]上连续,在(0,2)内可导,且φ(0)=φ(1)=φ(2)=0,因此φ(x)在[0,1]和[1,2]上都满足罗尔定理的条件,则存在ξ1∈(0,1),ξ2∈(1,2),使得φ'(ξ1)=φ'(ξ2)=0.
则φ(x)在[0,2]上连续,在(0,2)内可导,且φ(0)=φ(1)=φ(2)=0,因此φ(x)在[0,1]和[1,2]上都满足罗尔定理的条件,则存在ξ1∈(0,1),ξ2∈(1,2),使得φ'(ξ1)=φ'(ξ2)=0.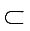 (0,2),使得φ''(ξ)=0.而φ'''(x)=f'''(x)-9,所以f'''(ξ)=9.
(0,2),使得φ''(ξ)=0.而φ'''(x)=f'''(x)-9,所以f'''(ξ)=9.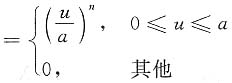
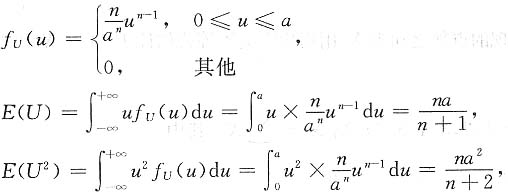
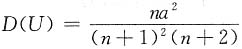 .
.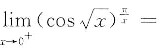 ______.
______.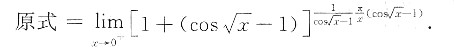
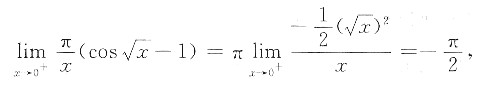
 令随机变量
令随机变量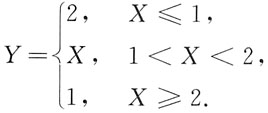 求:
求: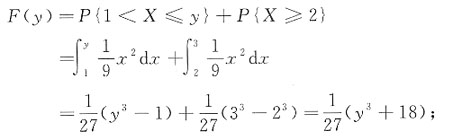
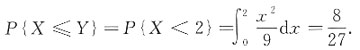
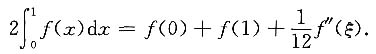
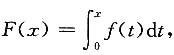 则F(x)三阶连续可导且F'(x)=f(x),由泰勒公式得
则F(x)三阶连续可导且F'(x)=f(x),由泰勒公式得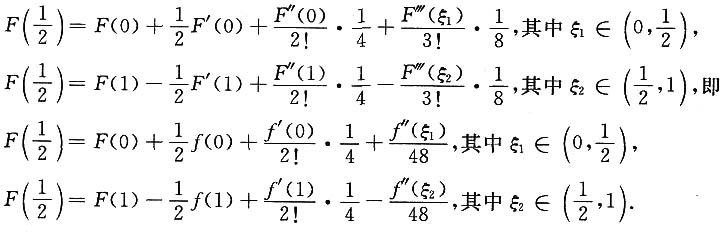
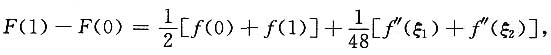
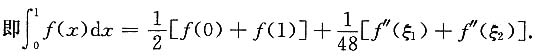
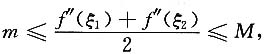
 (0,1),使得
(0,1),使得