一、选择题下列每题给出的四个选项中,只有一个选项是符合题目要求的.1. 已知α,β,γ
1,γ
2,γ
3均为4维列向量,若|A|=|α,γ
1,γ
2,γ
3|=3,|B|=|β,γ
1,γ
2,γ
3|=1,则|A+2B|=______
A B C D
A
[解析] 由A+2B=(α+2β,3γ1,3γ2,3γ3)
知|A+2B|=27|α+2β,γ1,γ2,γ3|
=27(|A|+2|B|)=135.
3. 设A是n阶方阵,线性方程组AX=0有非零解,则线性非齐次方程组A
TX=b对任意b=(b
1,b
2,…,b
n)
T______.
- A.不可能有唯一解
- B.必有无穷多解
- C.无解
- D.或有唯一解,或有无穷多解
A B C D
A
[考点] 线性方程组的解
[解析] 因为AX=0有非零解,而A为n阶方阵,所以|A|=|AT|=0.因此r(AT)<n.于是线性非齐次方程组ATX=b在r(A|b)=r(AT)时有无穷多解;在r(AT|b)>r(AT)时无解.故对任何b,ATX=b不可能有唯一解.所以选(A).
5. 设A为四阶实对称矩阵,且A
2+2A-3E=0.若R(A-E)=1,则二次型x
TAx在正交变换下的标准形为______
A.

B.

C.

D.

A B C D
A
[解析] 由A
2+2A-3E=0,得(A-E)(A+3E)=0,
∴R(A-E)+R(A+3E)≤4.
又
R(A-E)+R(A+3E)=R(E-A)+R(A+3E)
≥R(E-A+A+3E)
=R(4E)=R(E)=4,
∴R(A-E)+R(A+3E)=4.则R(A+3E)=3.
于是|A-E|=0,这表明1是A的特征值;
|A+3E|=0,这表明-3是A的特征值.
于是(A-E)x=0有3个线性无关的特征向量,λ=1为A的三重特征值;
(A+3E)x=0仅有1个线性无关的特征向量,λ=-3为A的一重特征值;
于是,四阶方阵A的特征值为1,1,1,-3,二次型x
TAx经正交变换后的标准形为

.
选A.
7. 设函数f(x),g(x)定义在(-1,1)内,且都在x=0处连续,若
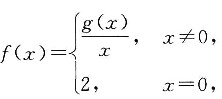
则______.
A.

B.
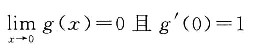
C.
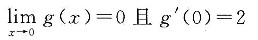
D.
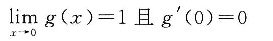
A B C D
C
[考点] 函数连续及导数定义.
[解析] 根据极限确定函数的性质.
因为函数f(x)在x=0处连续,则
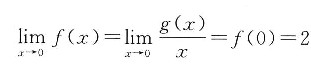
;因为函数g(x)在x=0处连续,则g(0)=0.又
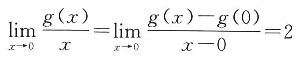
,则g'(0)=2.故应选C.
9. 设向量组(Ⅰ):α
1,α
2,…,α
s的秩为r
1,向量组(Ⅱ):β
1,β
2,…,β
s的秩为r
2,且向量组(Ⅱ)可由向量组(Ⅰ)线性表出,则______.
- A.α1+β1,α2+β2,…,αs+βs的秩为r1+r2
- B.向量组α1-β1,α2-β2,…,αs-βs的秩为r1-r2
- C.向量组α1,α2,…,αs,β1,β2,…,βs的秩为r1+r2
- D.向量组α1,α2,…,αs,β1,β2,…,βs的秩为r1
A B C D
D
[考点] 向量
[解析] 因为向量组β1,β2,…,βs可由向量组α1,α2,…,αs线性表出,所以向量组α1,α2,…,αs与向量组{α1,α2,…,αs;β1,β2,…,βs}等价,应选D.
10. 把当x→0时的无穷小量α=ln(1+x
2)-ln(1-x
4),
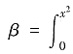
tantdt,γ=arctanx-x排列起来,使排在后面的是前一个的高阶无穷小,则正确的排列次序是
- A.α,β,γ.
- B.γ,α,β.
- C.α,γ,β.
- D.γ,β,α.
A B C D
C
[解析] 我们分别确定当x→0时,α、β、γ分别是x的几阶无穷小.当x→0时
α=ln(1+x
2)-ln(1-x
4)~x
2,
因为ln(1+x
2)~x
2 ln(1-x
4)~-x
4=0(x
2)
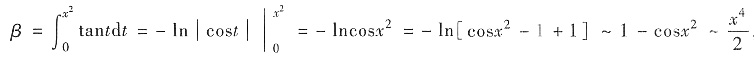
又由
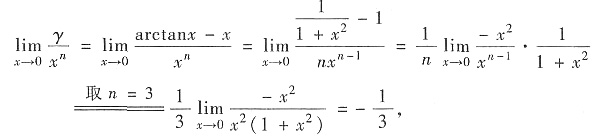
可知当x→0时
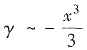
这表明当x一0时,α是关于x的2阶无穷小量,β是关于x的4阶无穷小量,而y是关于x的3阶无穷小量.按题目的要求,它们应排成α,γ,β的次序.故应选(C).
三、解答题本题共70分.解答应写出文字说明、证明过程或演算步骤.1. 设函数f(x)连续,
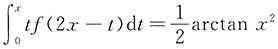
,f(1)=1,求
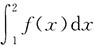
.
解:令u=2x-t,则dt=-du,有
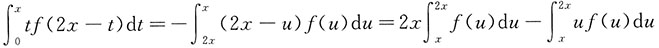
从而
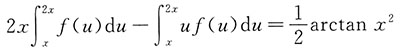
两边对x求导,得
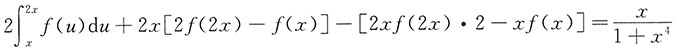
故
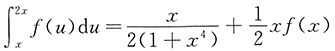
令x=1,得
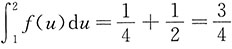
.
[考点] 不定积分、定积分、反常积分
2. 求
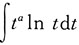
(a为常数).
3. 设A为n阶矩阵,证明:r(A)=1的充分必要条件是存在n维非零列向量α,β,使得A=αβ
T.
[证明] 设r(A)=1,则A为非零矩阵且A的每行元素都成比例,
令
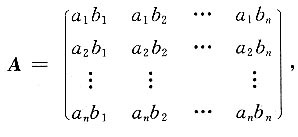
于是
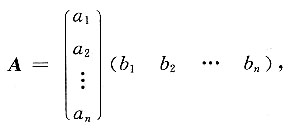
令
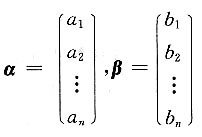
,故A=αβ
T,显然α,β为非零向量.设A=αβ
T,其中α,β为非零向量,则A为非零矩阵,于是r(A)≥1,又r(A)=r(αβ
T)≤r(α)=1,故r(A)=1.
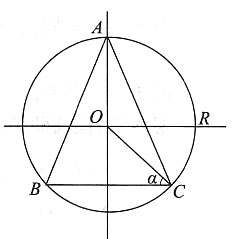
4. 在半径为R的球内作内接正圆锥体,试求其最大体积.
如下图所示,设圆半径OC与内接正圆锥底直径BC的夹角为α,则内接正圆锥的底面半径为
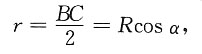
高为h=R(1+sinα),其中
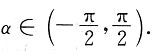
内接正圆锥的体积为
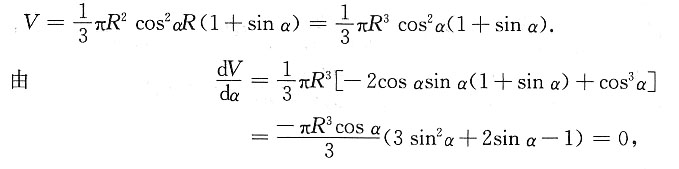
得
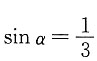
.故当内接正圆锥的底面直径为
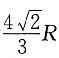
、高为
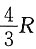
时,其体积最大,最大体积为
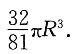
5. 设α
1,α
2分别为A的属于不同特征值λ
1,λ
2的特征向量,证明:α
1+α
2不是A的特征向量.
证明:反证法.若α1+α2是A的属于特征值λ的特征向量,则有
A(α1+α2)=λ(α1+α2)
因为
Aα1=λ1α1,Aα2=λ2α2
所以
(λ1-λ)α1+(λ2-λ)α2=0
而α1,α2线性无关,于是λ1=λ2=λ,矛盾,故α1+α2不是A的特征向量.
[考点] 特征值与特征向量
6. 计算积分
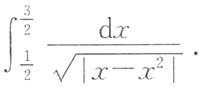
 则f(x)在x=0处
则f(x)在x=0处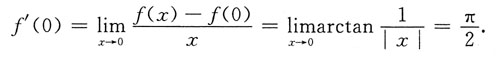
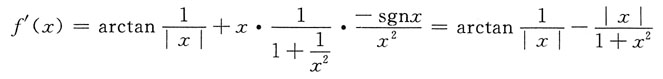
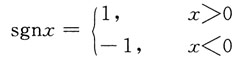
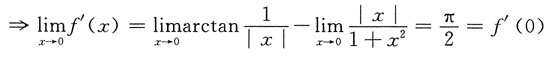 即f'(x)在x=0处连续.因此,选D.
即f'(x)在x=0处连续.因此,选D.



 .
.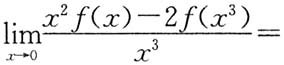
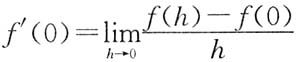 ,有
,有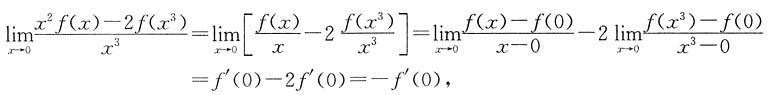
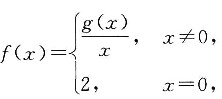 则______.
则______.
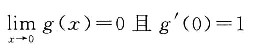
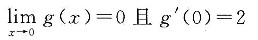
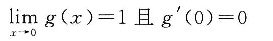
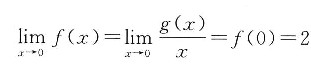 ;因为函数g(x)在x=0处连续,则g(0)=0.又
;因为函数g(x)在x=0处连续,则g(0)=0.又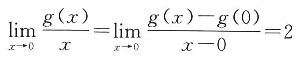 ,则g'(0)=2.故应选C.
,则g'(0)=2.故应选C.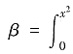 tantdt,γ=arctanx-x排列起来,使排在后面的是前一个的高阶无穷小,则正确的排列次序是
tantdt,γ=arctanx-x排列起来,使排在后面的是前一个的高阶无穷小,则正确的排列次序是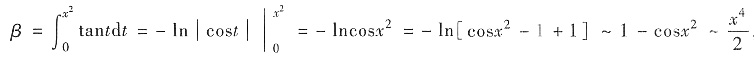
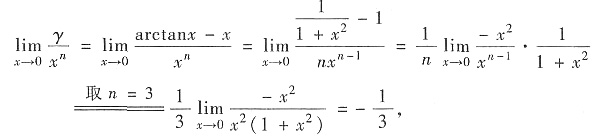
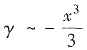
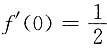 ,则z=f(4x2-y2)在点(1,2)处的全微分dz|(1,2)=______.
,则z=f(4x2-y2)在点(1,2)处的全微分dz|(1,2)=______.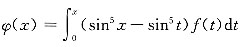 的导数与x5为等价无穷小,则f(0)=______.
的导数与x5为等价无穷小,则f(0)=______.
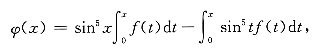
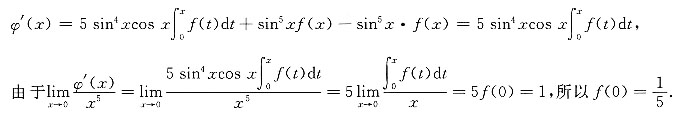

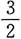
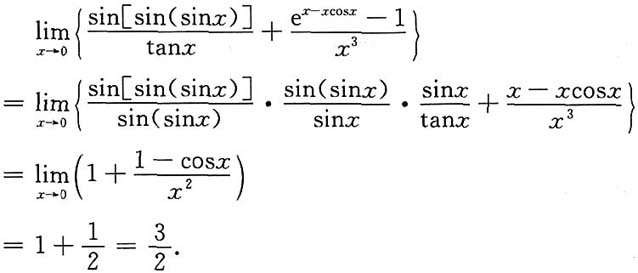
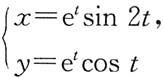 在点(0,1)处的法线方程为______.
在点(0,1)处的法线方程为______.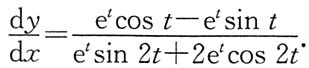
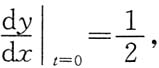
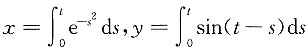 ,则
,则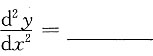 .
. ,故
,故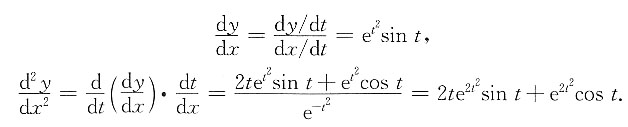
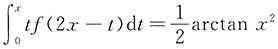 ,f(1)=1,求
,f(1)=1,求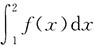 .
.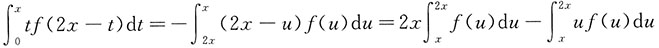
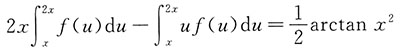
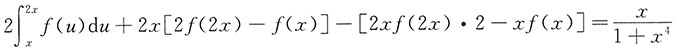
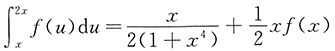
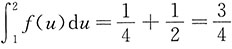 .
.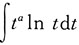 (a为常数).
(a为常数).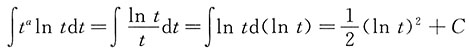
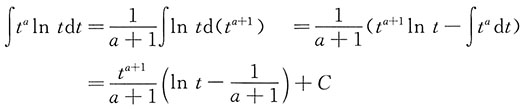
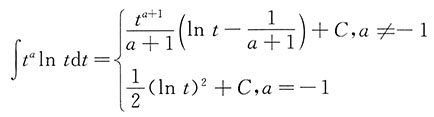
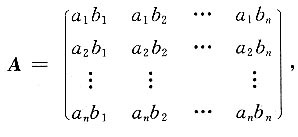 于是
于是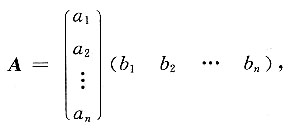 令
令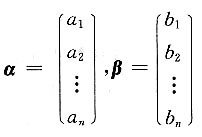 ,故A=αβT,显然α,β为非零向量.设A=αβT,其中α,β为非零向量,则A为非零矩阵,于是r(A)≥1,又r(A)=r(αβT)≤r(α)=1,故r(A)=1.
,故A=αβT,显然α,β为非零向量.设A=αβT,其中α,β为非零向量,则A为非零矩阵,于是r(A)≥1,又r(A)=r(αβT)≤r(α)=1,故r(A)=1.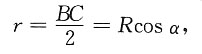
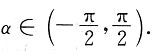
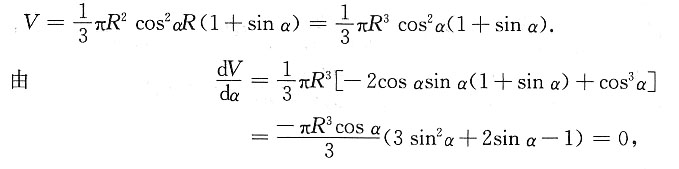
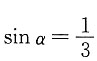 .故当内接正圆锥的底面直径为
.故当内接正圆锥的底面直径为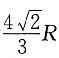 、高为
、高为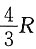 时,其体积最大,最大体积为
时,其体积最大,最大体积为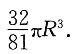
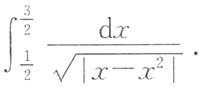
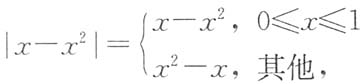
 因此
因此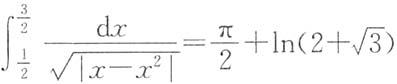 .
.