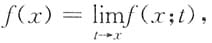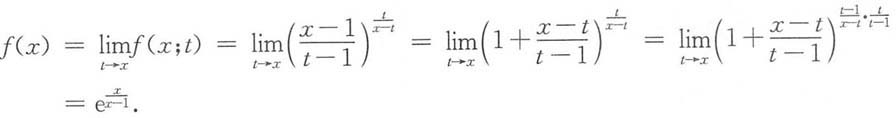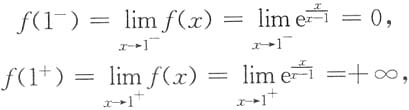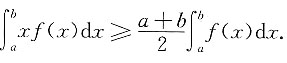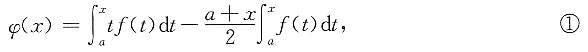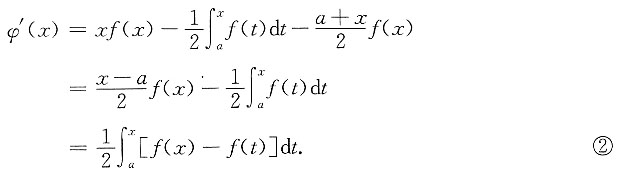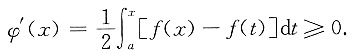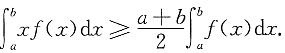一、选择题(下列每题给出的四个选项中,只有一个选项是符合题目要求的.)1. 将一枚均匀硬币连续抛n次,以A表示“正面最多出现一次”,以B表示“正面和反面各至少出现一次”,则______
A.n=2时,A与B相互独立.
B.n=2时,A

B.
C.n=2时,A与B互不相容.
D.n=3时,A与B相互独立.
A B C D
D
[解析] 当n=2时,
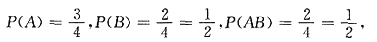
由P(AB)≠P(A)P(B)知A与B不独立,
又P(A)>P(B),故
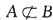
(若A
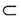
B,则P(A)≤P(B),矛盾).
当n=3时,
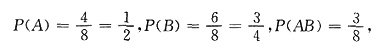
由上知P(AB)=P(A)P(B),因此A与B相互独立,故应选D.
2. 设
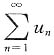
条件收敛,且
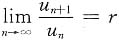
,则______.
- A.|r|<1
- B.|r|>1
- C.r=-1
- D.r=1
A B C D
C
[解析] 因为
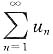
条件收敛,所以级数
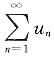
一定不是正项或负项级数,故r≤0.
若|r|<1,则
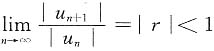
,级数
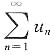
绝对收敛,矛盾;
若|r|>1,则
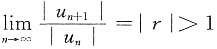
,存在充分大的N,当n>N时,{|u
n|}单调增加,
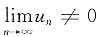
,于是
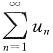
发散,矛盾,故|r|=1,再由r≤0得r=-1,选C.
3. 当x→0时,f(x)=x-sinax与g(x)=x
2ln(1-bx)是等价无穷小,则______.
A.
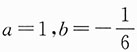
B.
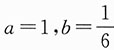
C.
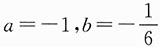
D.
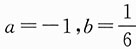
A B C D
A
[考点] 用等价无穷小确定未知参数.
[解析] 根据等价无穷小的定义,通过极限确定未知参数的值.
因为
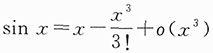
,由题意得
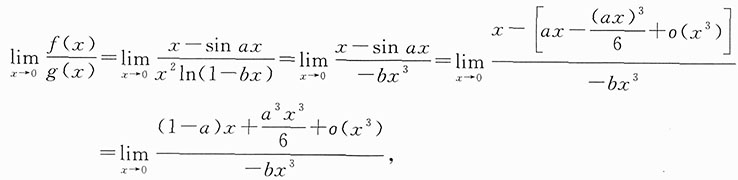
要使极限存在且等于1,则1-a=0且
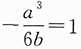
,解得a=1,
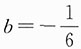
,故应选A.
根据等价无穷小的定义转化为函数的极限求解待定参数是重要内容,具体求解极限时,泰勒公式是简单的方法.
4. 设f(x)=|x|,g(x)=x
2-x,则等式f[g(x)]=g[f(x)]成立时,x的变化范围______
- A.(-∞,1]∪{0}.
- B.(-∞,0].
- C.[0,+∞).
- D.[1,+∞)∪{0}.
A B C D
D
[解析] f[g(x)]=|g(x)|=|x
2-x|,
g[f(x)]=f
2(x)-f(x)=|x|
2-|x|=x
2-|x|.
由f[g(x)]=g[f(x)],得|x
2-x|=x
2-|x|.
当x
2≥x,即x≤0或者x≥1时,有x
2-x=x
2-|x|,即
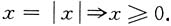
综合得x≥1.
当x
2≤x,即1≥x≥0时,
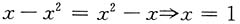
或x=0.
综上所述,当x≥1或x=0时,f[g(x)]=g[f(x)].
5. 设f(x)为连续的偶函数,F(x)为f(x)的原函数,且

则F(x)等于______
A.
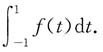
B.

C.
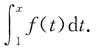
D.
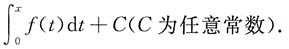
A B C D
B
[解析] 因为f(x)为偶函数,所以
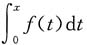
为奇函数,且
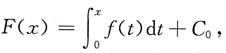
又

即C
0=0,
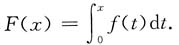
6. 设总体X~P(λ)(λ为未知参数),X
1,X
2,…,X
n是来自总体X的简单随机样本,其均值与方差分别为
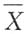
与S
2,则为使
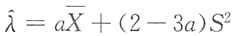
是λ的无偏估计量,常数a应为______
A.-1
B.0
C.
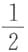
D.1
A B C D
C
[解析] 要使
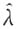
是λ的无偏估计量,应有
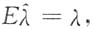
即

由于
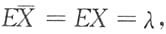
E(S
2)=DX=λ,将它们代入①得aλ+(2-3a)λ=λ,即
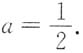
因此本题选C.
7. A是n阶方阵,则A相似于对角阵的充分必要条件是______
- A.A有n个不同的特征值
- B.A有n个不同的特征向量
- C.A的每个ri重特征值λi,r(λiE-A)=n-ri
- D.A是实对称矩阵
A B C D
C
[解析] A相似于对角阵
A有n个线性无关特征向量
对每个r
i重特征值λ
i,r(λ
iE-A)=n-r
i,即有r
i个线性无关特征向量(共n个线性无关特征向量).
(A),(D)是充分条件,但非必要,(B)是必要条件,但不充分,n个不同的特征向量,并不一定线性无关.
8. 设X
1,X
2,…,X
n为来自总体X的简单随机样本,其中
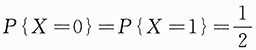
,Φ(x)表示标准正态分布函数,则利用中心极限定理可得
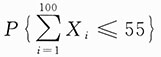
的近似值为______.
- A.1-Φ(1)
- B.Φ(1)
- C.1-Φ(0.2)
- D.Φ(0.2)
A B C D
B
[考点] 考查中心极限定理,属基本知识点.
[解析] 利用中心极限定理,结合数字特征计算.
因为

,所以X服从0-1分布,其中
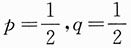
,故
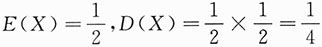
.
又因为X
1,X
2,…,X
n为来自总体X的简单随机样本,所以
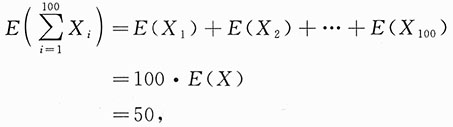
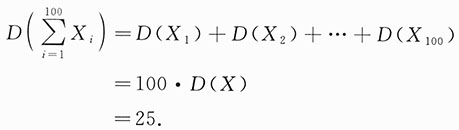
由中心极限定理有
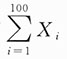
近似服从于N(50,25),所以
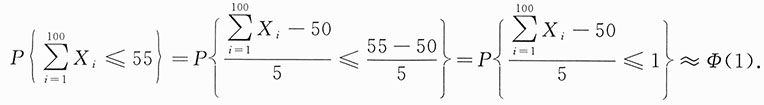
故应选B.
本题的解法用到了列维-林德伯格定理,此为一般方法.因为在本题已知条件中给出的是0-1分布,而0-1分布之和是二项分布,故应用如下棣莫弗-拉普拉斯定理解决更加简便.
因为
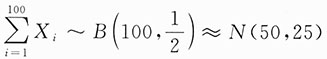
,所以
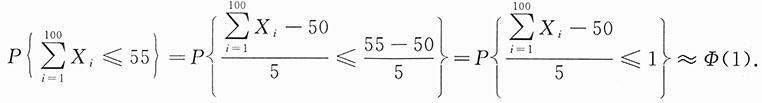
9. 设总体X服从正态分布N(0,σ
2)(σ
2已知),X
1,X
2,…,X
n是取自总体X的简单随机样本,S
2为样本方差,则______
A.
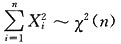
B.
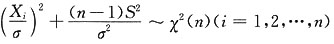
C.
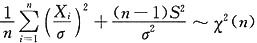
D.
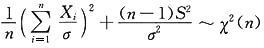
A B C D
D
[解析] 由题设知X
i~N(0,σ
2),
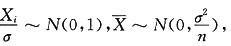
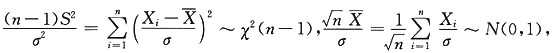
故
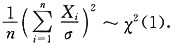
又
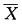
与S
2独立,故有
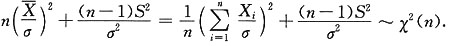
二、填空题1. 差分方程Δ
2y
x-y
x=5的解为______.
yx=C·2x-5
[解析] Δ2yx=Δ(Δyx)=Δyx+1-Δyx=(yx+2-yx+1)-(yx+1-yx)=yx+2-2)yx+1+yx,因此原差分方程可化简为yx+2-2yx+1=5.
齐次方程yx+2-2yx+1=0的通解为Yx=C·2x.
设非齐次方程的特解为y*x=A,代入非齐次方程中,可得A=-5.
故非齐次方程,即原差分方程的通解为Yx=Yx+y*x=C·2x-5.
2. 设
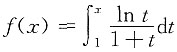
,则
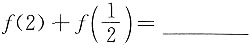
.
3. 设

|A|>0且A
*的特征值为-1,-2,2,则a
11+a
22+a
33=______.
-2
[解析] 因为|A
*|=|A|
2=4,且|A|>0,所以|A|=2,又AA
*=|A|E=2E,所以A
-1=
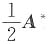
,从而A
-1的特征值为
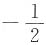
,-1,1,根据逆矩阵之间特征值的倒数关系,则A的特征值为-2,-1,1,于是a
11+a
22+a
33=-2-1+1=-2.
4. 设a>0,
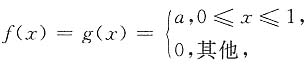
而D表示整个平面,则
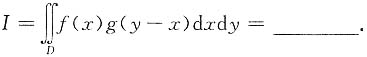
a2
[解析] 由
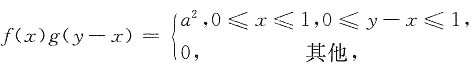
得
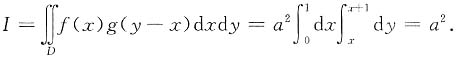
5. 设随机变量X的数学期望EX=75,方差DX=5,由切比雪夫不等式估计得P{|X-75|≥k}≤0.05,则k=______.
10
[解析]
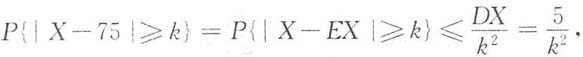
于是由题设得
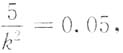
即k=10.
6. 一射手对同一目标独立地进行四次射击,若至少命中一次的概率为
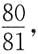
则该射手的命中率为______.
[解析] 独立重复试验.至少命中一次的对立事件是四次都没有命中.四次都没有命中的概率是
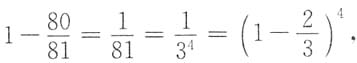
所以该射手的命中率为
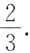
三、解答题(共70分.解答应写出文字说明、证明过程或演算步骤.)设X与Y相互独立,且均服从(-1,1)上的均匀分布.1. 试求X和Y的联合分布函数;
[解] X,Y的联合概率
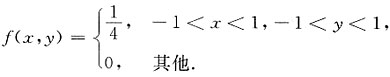
当-1<x<1,-1<y<1时,
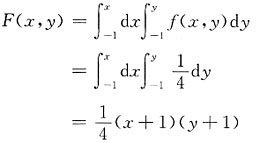
∴X、Y的联合分布函数为
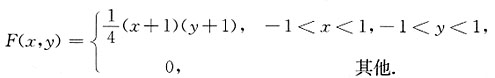
2. 试求Z=X+Y的密度函数.
[解] 求Z的概率密度,用密度函数法.
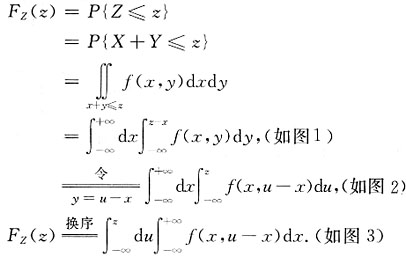
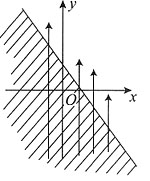
图1
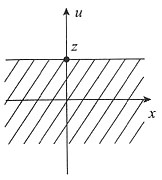
图2
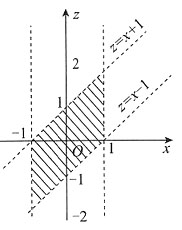
图3
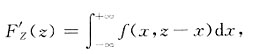
-1<x<1,-1<z-x<1,
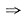
-1<x<1,x-1<z<x+1,
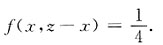
ⅰ)-2<z<0,
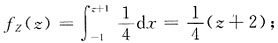
ⅱ)0≤z<2,
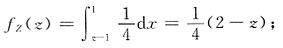
ⅲ)在其他点,f
Z(z)=0.
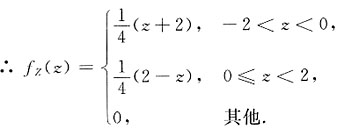

3. 求在Y=y的条件下,X的条件概率密度函数;
解:当0<y<1时,
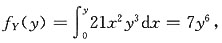

4. X与Y是否相互独立?说明理由;
解:
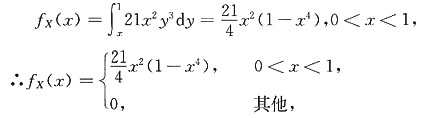
显然f
x|y(x|y)≠f
X(x),所以X,Y不独立,
或者说F
X(x)·f
Y(y)≠f(x,y),X,Y不独立.
5. 求
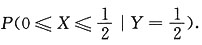
解:
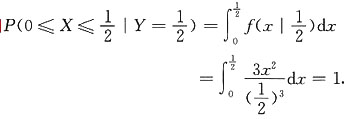
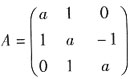 ,且A3=0。
,且A3=0。6. 求a的值;
解:
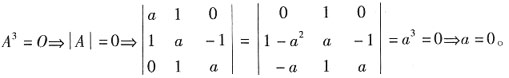
7. 若矩阵X满足X-XA
2-AX+AXA
2=E,其中E为3阶单位矩阵,求X。
解:由题意知
X-XA
2-AX+AXA
2=E
X(E-A
2)-AX(E-A
2)=E
(E-A)X(E-A
2)=E
X=(E-A)
-1(E-A
2)
-1,
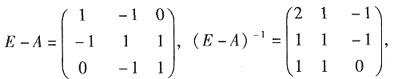
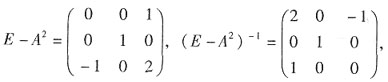
故
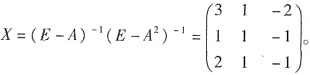
[考点] 矩阵的计算及矩阵方程的化简。
8. 计算
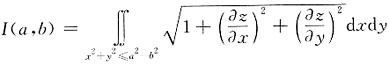
,其中z是由方程x
2+y
2+z
2=a
2所确定的x,y的函数,且0<b≤z≤a.
[解]
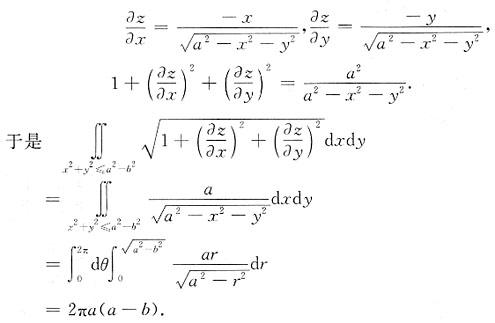
9. 设
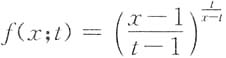
,其中(x-1)(t-1)>0,x≠t,函数f(x)由下列表达式确定,
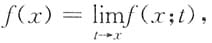
求出f(x)的连续区间和间断点,并研究f(x)在间断点处的左右极限.
解:
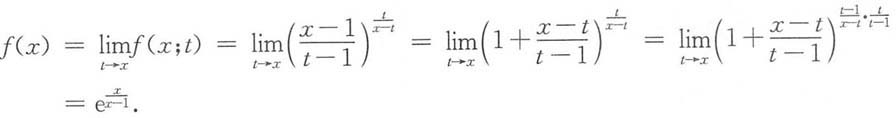
显然x=1为间断点,连续区间(-∞,1)∪(1,+∞).
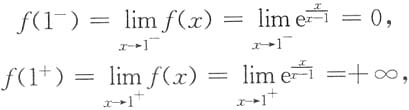
所以x=1为无穷间断点.
10. 设f(x)在区间[a,b]上为连续的单调增函数,证明:
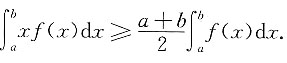
证明:令
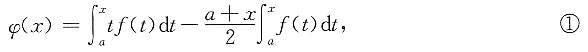
有φ(a)=0及
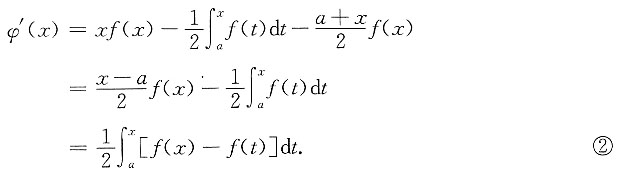
由于f(x)在区间[a,b]上为单调增函数,所以当a≤t≤x时f(t)≤f(x),从而由②式知
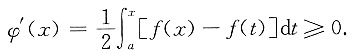
再由φ(a)=0得φ(b)≥0.所以由①式有
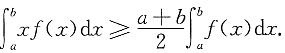
证毕.
 B.
B.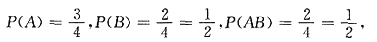
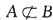 (若A
(若A B,则P(A)≤P(B),矛盾).
B,则P(A)≤P(B),矛盾).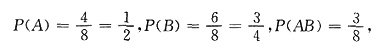
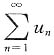 条件收敛,且
条件收敛,且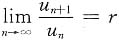 ,则______.
,则______.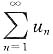 条件收敛,所以级数
条件收敛,所以级数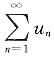 一定不是正项或负项级数,故r≤0.
一定不是正项或负项级数,故r≤0.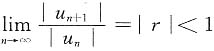 ,级数
,级数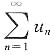 绝对收敛,矛盾;
绝对收敛,矛盾;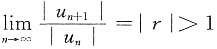 ,存在充分大的N,当n>N时,{|un|}单调增加,
,存在充分大的N,当n>N时,{|un|}单调增加,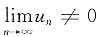 ,于是
,于是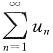 发散,矛盾,故|r|=1,再由r≤0得r=-1,选C.
发散,矛盾,故|r|=1,再由r≤0得r=-1,选C.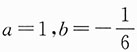
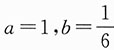
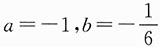
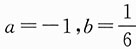
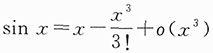 ,由题意得
,由题意得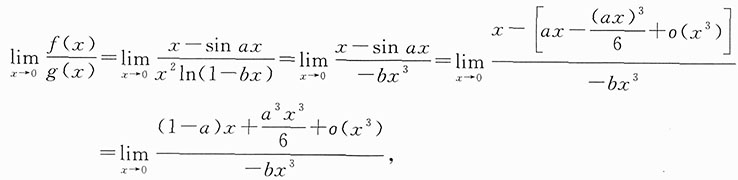
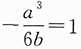 ,解得a=1,
,解得a=1,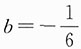 ,故应选A.
,故应选A.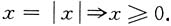
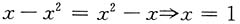 或x=0.
或x=0. 则F(x)等于______
则F(x)等于______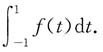

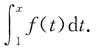
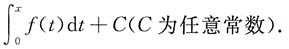
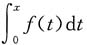 为奇函数,且
为奇函数,且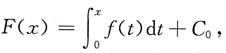 又
又 即C0=0,
即C0=0,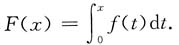
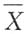 与S2,则为使
与S2,则为使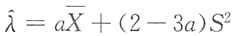 是λ的无偏估计量,常数a应为______
是λ的无偏估计量,常数a应为______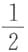
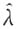 是λ的无偏估计量,应有
是λ的无偏估计量,应有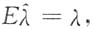 即
即
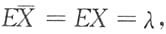 E(S2)=DX=λ,将它们代入①得aλ+(2-3a)λ=λ,即
E(S2)=DX=λ,将它们代入①得aλ+(2-3a)λ=λ,即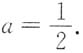 因此本题选C.
因此本题选C. A有n个线性无关特征向量
A有n个线性无关特征向量 对每个ri重特征值λi,r(λiE-A)=n-ri,即有ri个线性无关特征向量(共n个线性无关特征向量).
对每个ri重特征值λi,r(λiE-A)=n-ri,即有ri个线性无关特征向量(共n个线性无关特征向量).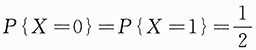 ,Φ(x)表示标准正态分布函数,则利用中心极限定理可得
,Φ(x)表示标准正态分布函数,则利用中心极限定理可得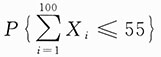 的近似值为______.
的近似值为______. ,所以X服从0-1分布,其中
,所以X服从0-1分布,其中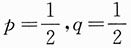 ,故
,故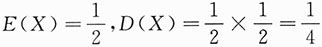 .
.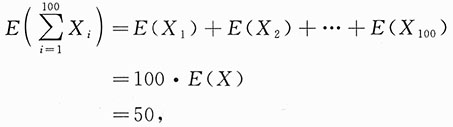
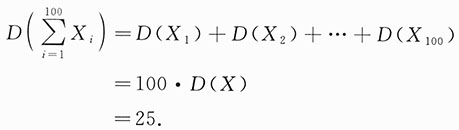
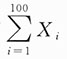 近似服从于N(50,25),所以
近似服从于N(50,25),所以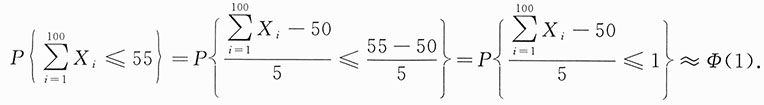
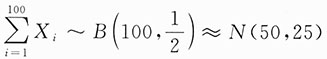 ,所以
,所以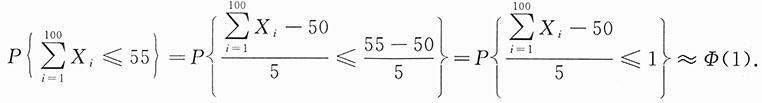
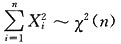
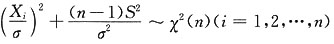
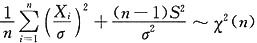
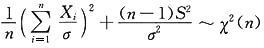
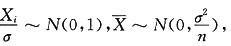
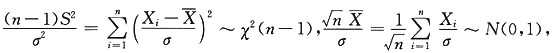
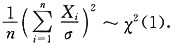
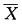 与S2独立,故有
与S2独立,故有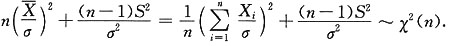
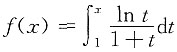 ,则
,则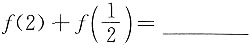 .
.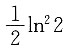
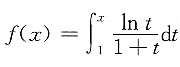 ,从而当x>0时,
,从而当x>0时,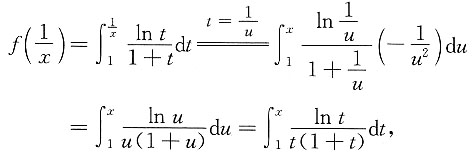
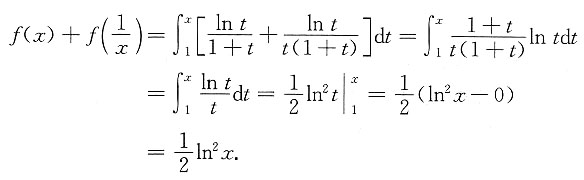
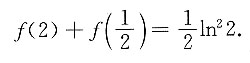
 |A|>0且A*的特征值为-1,-2,2,则a11+a22+a33=______.
|A|>0且A*的特征值为-1,-2,2,则a11+a22+a33=______.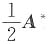 ,从而A-1的特征值为
,从而A-1的特征值为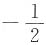 ,-1,1,根据逆矩阵之间特征值的倒数关系,则A的特征值为-2,-1,1,于是a11+a22+a33=-2-1+1=-2.
,-1,1,根据逆矩阵之间特征值的倒数关系,则A的特征值为-2,-1,1,于是a11+a22+a33=-2-1+1=-2.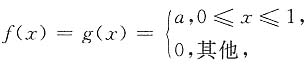 而D表示整个平面,则
而D表示整个平面,则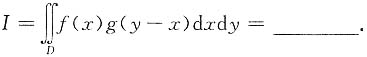
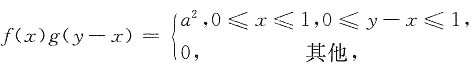
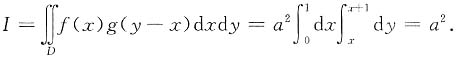
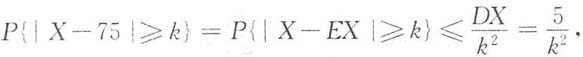 于是由题设得
于是由题设得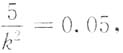 即k=10.
即k=10.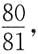 则该射手的命中率为______.
则该射手的命中率为______.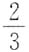
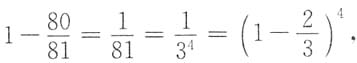 所以该射手的命中率为
所以该射手的命中率为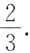
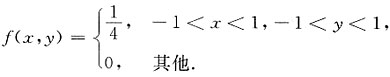
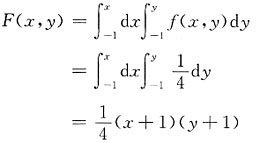
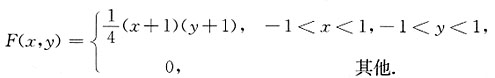
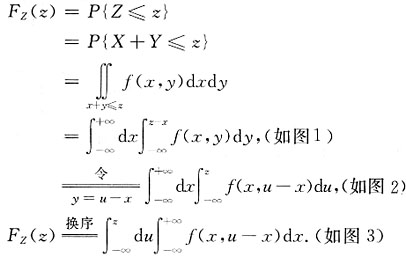



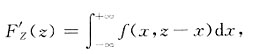
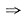 -1<x<1,x-1<z<x+1,
-1<x<1,x-1<z<x+1,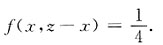
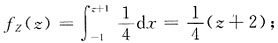
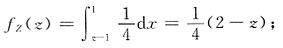
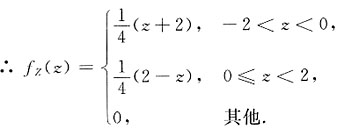

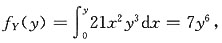

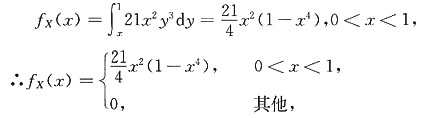
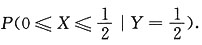
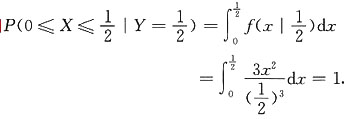
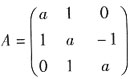 ,且A3=0。
,且A3=0。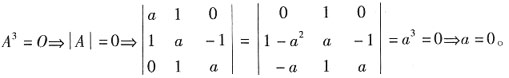
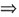 X(E-A2)-AX(E-A2)=E
X(E-A2)-AX(E-A2)=E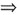 (E-A)X(E-A2)=E
(E-A)X(E-A2)=E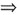 X=(E-A)-1(E-A2)-1,
X=(E-A)-1(E-A2)-1,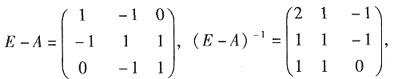
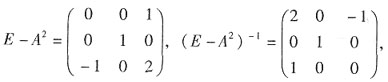
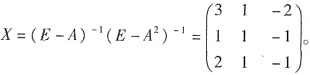
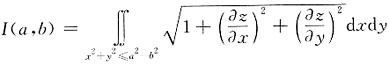 ,其中z是由方程x2+y2+z2=a2所确定的x,y的函数,且0<b≤z≤a.
,其中z是由方程x2+y2+z2=a2所确定的x,y的函数,且0<b≤z≤a.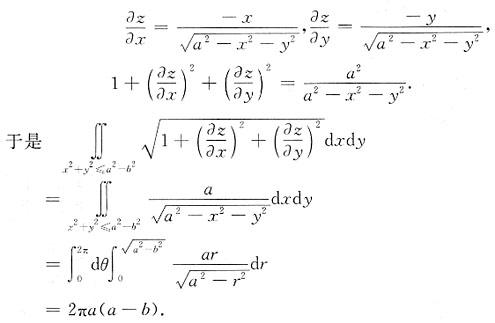
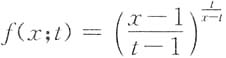 ,其中(x-1)(t-1)>0,x≠t,函数f(x)由下列表达式确定,
,其中(x-1)(t-1)>0,x≠t,函数f(x)由下列表达式确定,