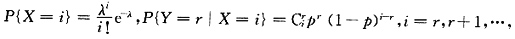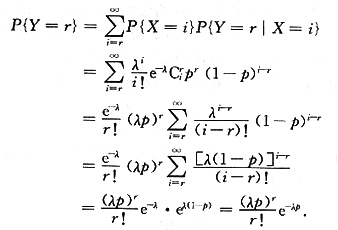一、选择题(下列每题给出的四个选项中,只有一个选项是符合题目要求的.)3. 积分
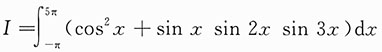
=______.
A B C D
B
[考点] 周期函数定积分的计算.
[解析] 利用周期函数的积分性质求解.
cos
2x,sinx,sin2x,sin3x都是以2π为周期的函数,则
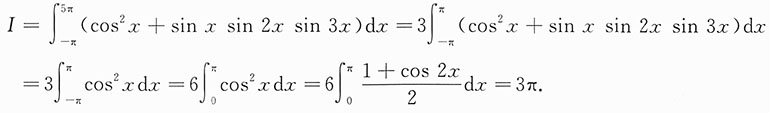
故应选B.
4. 设f"(x)在x=0处连续,且
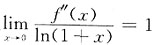
,则______
- A.f(0)是f(x)的极大值.
- B.f(0)是f(x)的极小值.
- C.(0,f(0))是曲线y=f(x)的拐点.
- D.f(0)不是f(x)的极值,(0,f(0))也不是曲线y=f(x)的拐点.
A B C D
C
[解析] 由
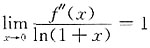
,得f"(0)=0,由极限保号定理,存在δ>0,当0<|x-0|<δ时,
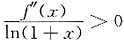
,即有
|
|
(-δ,0)
|
0
|
(0,δ)
|
| f"(x)
|
-
|
0
|
+
|
| f(x)
|
∩
|
拐点
|
∪
|
即(0,f(0))是曲线y=f(x)的拐点.
选C.
6. 设
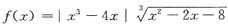
,则f(x)的不可导的点的个数______
A B C D
D
[解析]

f(x)的不可导的点首先应从|x(x+2)(x-2)|=0的点去考虑.取x=0,2,-2逐个讨论之.
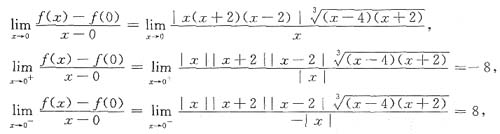
所以f'(0)不存在.同理f'(2)也不存在.
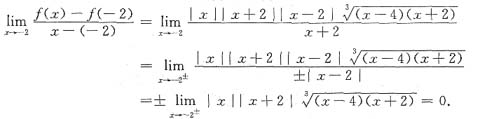
f'(-2)存在.再考虑
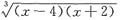
内为零即x=4处.
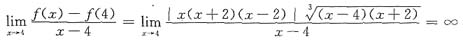
f'(4)不存在.共有3处f'(x)不存在.选D.
7. f(x)=xe
x的n阶麦克劳林公式为______
A.
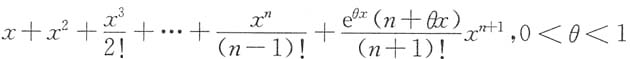
B.
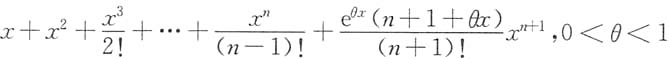
C.
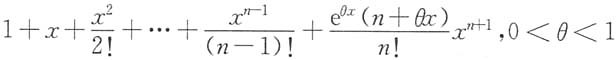
D.
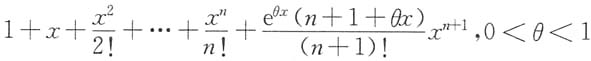
A B C D
B
[解析] 因为f(x)=xex,f(0)=0,f'(x)=ex(1+x),f'(0)=1,…,f(n)(x)=ex(n+x),f(n)(0)=n,f(n+1)(x)=ex(n+1+x),f(n+1)(θx)=eθx(n+1+θx),依次代入到泰勒公式,即得(B).
9. 设f(x)在区间(0,+∞)内可导,下述论断正确的是______
- A.设存在X>0,在区间(X,+∞)内f'(x)有界,则f(x)在(X,+∞)内亦必有界.
- B.设存在X>0,在区间(X,+∞)内f(x)有界,则f'(x)在(X,+∞)内亦必有界.
- C.设存在δ>0,在区间(0,δ)内f'(x)有界,则f(x)在(0,δ)内亦必有界.
- D.设存在δ>0,在区间(0,δ)内f(x)有界,则f'(x)在(0,δ)内亦必有界.
A B C D
C
[解析] 直接证明C是正确的,设f'(x)在(a,b)内有界,|f'(x)|≤M
1,当x∈(a,b)时,对于(a,b)内的任意两点x
0与x,固定x
0,则由中值定理得
f(x)=f(x
0)+f'(ξ)(x-x
0),
|f(x)|≤|f(x
0)|+M
1(b-a),对于x∈(a,b).
而右边是一确定的数,说明|f(x)|≤M(有界).即证明了:若f'(x)在(a,b)内有界,则f(x)在(a,b)内亦有界.所以如果在(a,b)内f(x)无界,则f'(x)在(a,b)内亦必无界.
其它A,B,D三项均可举出反例说明它们不正确.
A的反例:
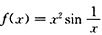
在区间(1,+∞)内无界,
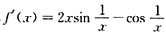
在区间(1,+∞)内却是有界的.这是因为

,所以
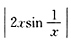
有界,又显然
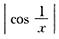
有界,所以|f'(x)|在(1,+∞)内有界.
B的反例:f'(x)=2xsinx
2在区间(0,+∞)内无界,但f(x)=-cosx
2在区间(0,+∞)内有界.
D的反例:
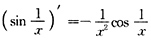
在区间(0,1)内无界,但
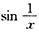
在区间(0,1)内却是有界的,
10. 设

,记
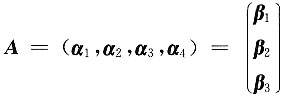
,且
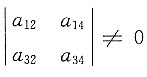
,

,下列结论:①r(A)=2;②α
2,α
4线性无关;③β
1,β
2,β
3线性相关;④α
1,α
2,α
3线性相关,正确的是_____
A B C D
D
[解析] 对于①,由
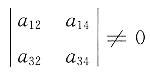
知,r(A)≥2,但

,不能得到r(A)<3(所有3阶子式全为0才可以得到r(A)<3),所以①不正确.
对于②,由

知,
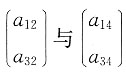
线性无关,于是增加分量得
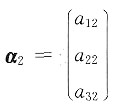
与
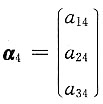
仍线性无关,所以②正确.
对于③,由

知,(a
11,a
12,a
13),(a
21,a
22,a
23),(a
31,a
32,a
33)线性相关,但增加分量得β
1,β
2,β
3不一定线性相关,故③不正确.
对于④,由

知,α
1,α
2,α
3线性相关,故④正确.
选D.
三、解答题(共70分.解答应写出文字说明、证明过程或演算步骤.)1. 证明:方阵A是正交矩阵,即AA
T=E的充分必要条件是:(1)A的列向量组组成标准正交向量组,即
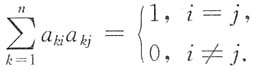
或(2)A的行向量组组成标准正交向量组,即
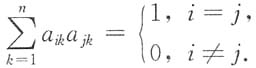
证明:设
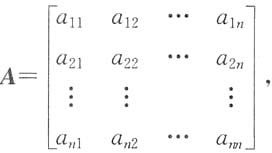
且A是正交矩阵.
(1)AA
T=E,A,A
T互为逆矩阵,有A
TA=E,故

(2)AA
T=E,即
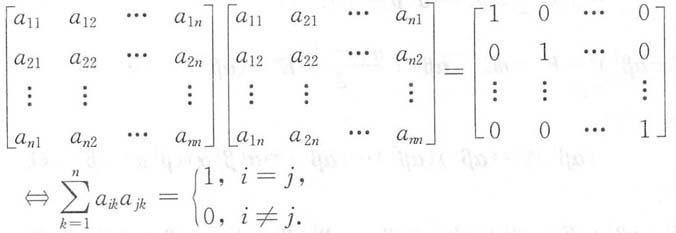
2. 写出f(x)的带拉格朗日余项的一阶麦克劳林公式;
解:对任意x∈[-a,a],

3. 证明:存在η∈[-a,a],使
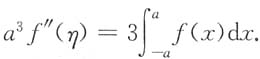
解:
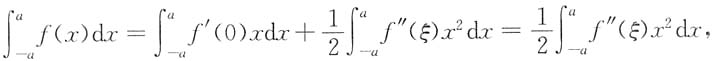
因为f"(x)在[-a,a]上连续,由最值定理:m≤f"(x)≤M,x∈[-a,a].
mx
2≤f"(ξ)x
2≤Mx
2,
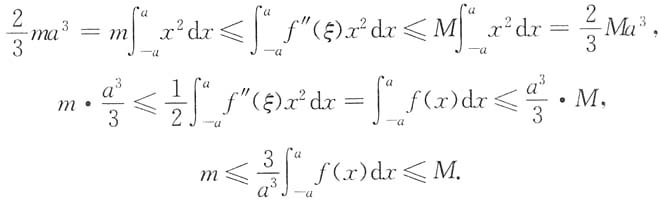
由介值定理,存在η∈[-a,a],使得
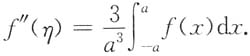
4. 求矩阵A的特征值.
解:因为α1,α2,α3线性无关,所以α1+α2+α3≠0,
由A(α1+α2+α3)=2(α1+α2+α3),得A的一个特征值为λ1=2;
又由A(α1-α2)=-(α1-α2),A(α2-α3)=-(α2-α3),得A的另一个特征值为λ2=-1.因为α1,α2,α3线性无关,所以α1-α2与α2-α3也线性无关,所以λ2=-1为矩阵A的二重特征值,即A的特征值为2,-1,-1.
5. 判断矩阵A可否对角化.
解:因为α1-α2,α2-α3为属于二重特征值-1的两个线性无关的特征向量,所以A一定可以对角化.
6. 求不定积分
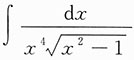
.
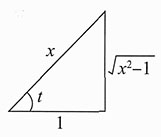
解:如图所示,令x=sect,则dx=sect tantdt,因而有
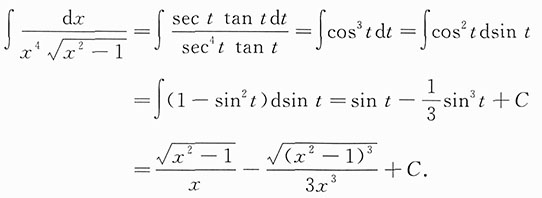
[考点] 无理根式不定积分求解.
[解析] 用第二换元积分法求解.
当被积函数中含有
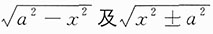
的因子时,常用三角代换求解——弦代换、切代换和割代换.
7. 设电子管寿命X的概率密度为
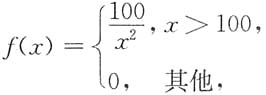
若一台收音机上装有三个这种电子管,求:
(1)使用的最初150小时内,至少有两个电子管被烧坏的概率;
(2)在使用的最初150小时内烧坏的电子管数Y的分布律;
(3)Y的分布函数.
解:Y为“在使用的最初150小时内烧坏的电子管数”,Y~B(3,p),其中
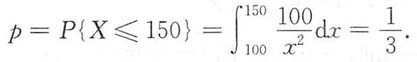
(1)所求概率为
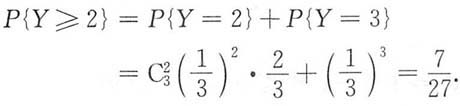
(2)Y的分布列为
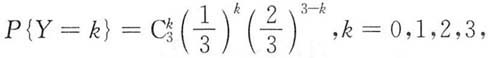
即
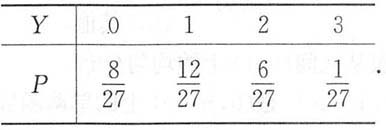
(3)Y的分布函数为
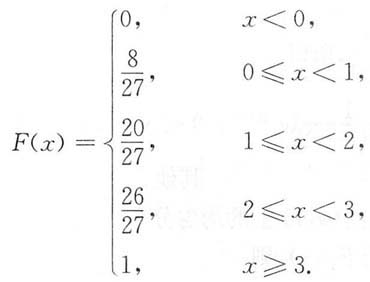
8. 设在某段时间内来到证券交易所的人数X服从参数为λ的泊松分布,每个来交易所的人购买A股的概率为p.假设股民之间是否购买A股相互独立,试求在该段时间内交易所X人中共有Y人购买A股的数学期望.
解:Y=r表示“有r个人买A股”,X=i表示“有i个人来到交易所”,i=r,r+1,…,
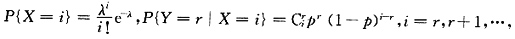
于是,由全概率公式有
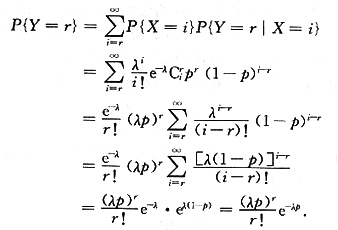
从此可看出X人中购买A股的人数Y服从参数为λp的泊松分布,所以EY=λp.
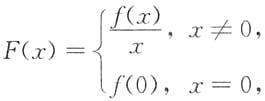 其中f(x)在x=0处可导,f'(0)≠0,f(0)=0,则x=0是F(x)的______
其中f(x)在x=0处可导,f'(0)≠0,f(0)=0,则x=0是F(x)的______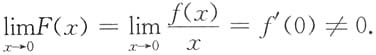
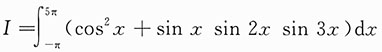 =______.
=______.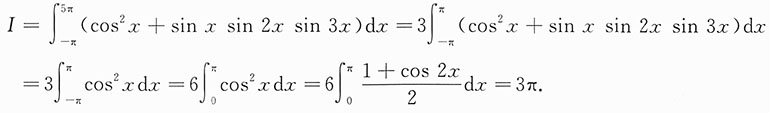
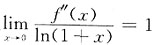 ,则______
,则______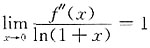 ,得f"(0)=0,由极限保号定理,存在δ>0,当0<|x-0|<δ时,
,得f"(0)=0,由极限保号定理,存在δ>0,当0<|x-0|<δ时,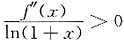 ,即有
,即有
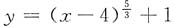 ______
______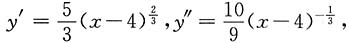 当x=4时y"不存在,且在x=4左右异号,所以(4,1)是拐点.虽然x=4时,y'=0,但在x=4左右y'不变号,故f(x)无极值点.
当x=4时y"不存在,且在x=4左右异号,所以(4,1)是拐点.虽然x=4时,y'=0,但在x=4左右y'不变号,故f(x)无极值点.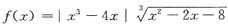 ,则f(x)的不可导的点的个数______
,则f(x)的不可导的点的个数______
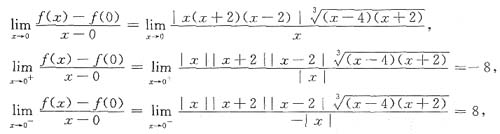
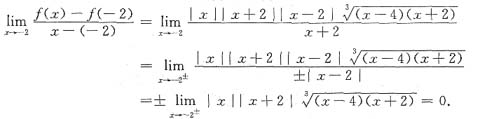
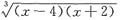 内为零即x=4处.
内为零即x=4处.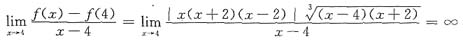
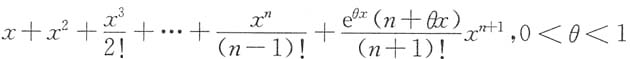
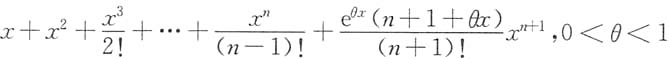
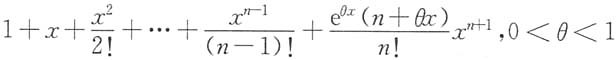
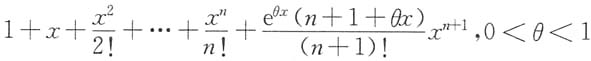
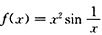 在区间(1,+∞)内无界,
在区间(1,+∞)内无界,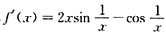 在区间(1,+∞)内却是有界的.这是因为
在区间(1,+∞)内却是有界的.这是因为 ,所以
,所以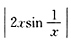 有界,又显然
有界,又显然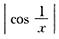 有界,所以|f'(x)|在(1,+∞)内有界.
有界,所以|f'(x)|在(1,+∞)内有界.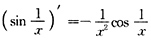 在区间(0,1)内无界,但
在区间(0,1)内无界,但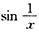 在区间(0,1)内却是有界的,
在区间(0,1)内却是有界的, ,记
,记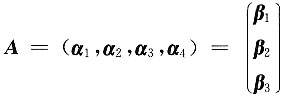 ,且
,且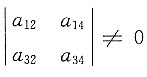 ,
, ,下列结论:①r(A)=2;②α2,α4线性无关;③β1,β2,β3线性相关;④α1,α2,α3线性相关,正确的是_____
,下列结论:①r(A)=2;②α2,α4线性无关;③β1,β2,β3线性相关;④α1,α2,α3线性相关,正确的是_____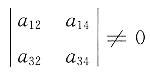 知,r(A)≥2,但
知,r(A)≥2,但 ,不能得到r(A)<3(所有3阶子式全为0才可以得到r(A)<3),所以①不正确.
,不能得到r(A)<3(所有3阶子式全为0才可以得到r(A)<3),所以①不正确. 知,
知,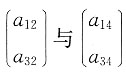 线性无关,于是增加分量得
线性无关,于是增加分量得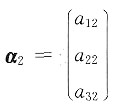 与
与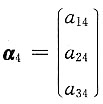 仍线性无关,所以②正确.
仍线性无关,所以②正确. 知,(a11,a12,a13),(a21,a22,a23),(a31,a32,a33)线性相关,但增加分量得β1,β2,β3不一定线性相关,故③不正确.
知,(a11,a12,a13),(a21,a22,a23),(a31,a32,a33)线性相关,但增加分量得β1,β2,β3不一定线性相关,故③不正确. 知,α1,α2,α3线性相关,故④正确.
知,α1,α2,α3线性相关,故④正确.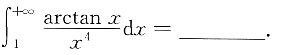
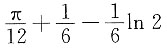
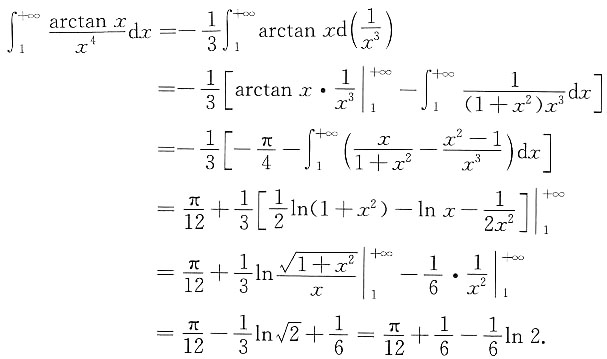
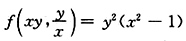 ,则dz=______.
,则dz=______.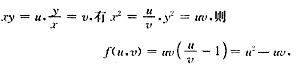
 ,则β1,β2,β3,β4均为方程组Ax=0的解.
,则β1,β2,β3,β4均为方程组Ax=0的解.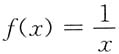 展开成的(x-1)的幂级数为______.
展开成的(x-1)的幂级数为______.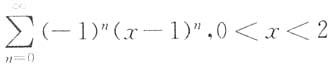
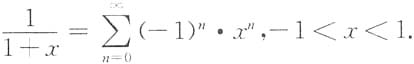 故
故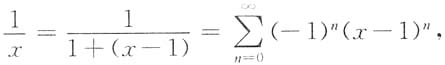 -1<x-1<1,即0<x<2.
-1<x-1<1,即0<x<2.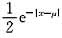 (-∞<x<+∞),X1,X2…,Xn为总体X的简单随机样本,其样本方差为S2,则E(S2)=______.
(-∞<x<+∞),X1,X2…,Xn为总体X的简单随机样本,其样本方差为S2,则E(S2)=______.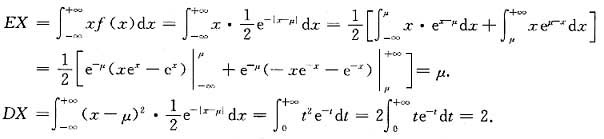
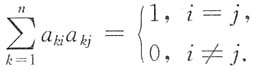 或(2)A的行向量组组成标准正交向量组,即
或(2)A的行向量组组成标准正交向量组,即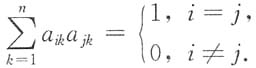
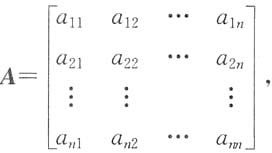 且A是正交矩阵.
且A是正交矩阵.
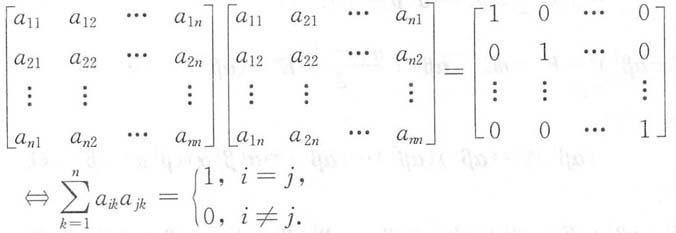

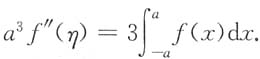
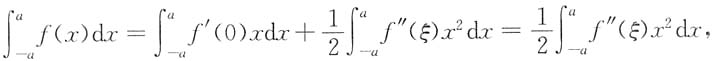
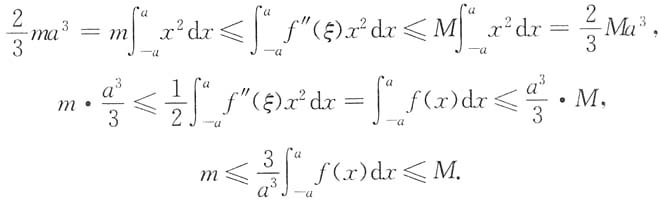
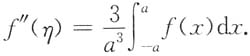
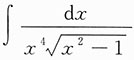 .
.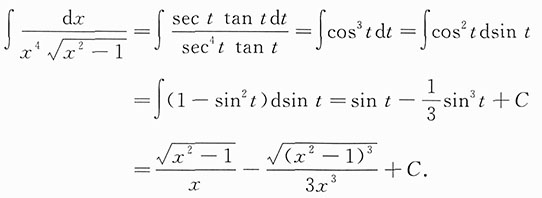
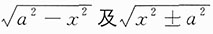 的因子时,常用三角代换求解——弦代换、切代换和割代换.
的因子时,常用三角代换求解——弦代换、切代换和割代换.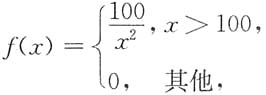 若一台收音机上装有三个这种电子管,求:
若一台收音机上装有三个这种电子管,求: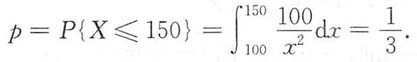
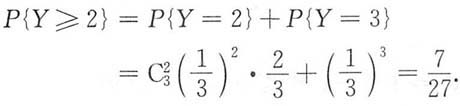
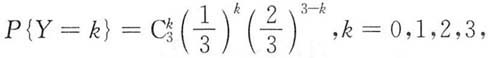 即
即