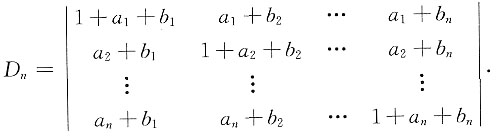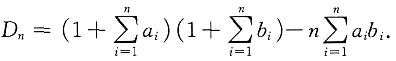一、选择题(下列每题给出的四个选项中,只有一个选项是符合题目要求的.)1. 曲线
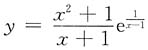
的渐近线的条数为______
A B C D
D
[解析] 因为
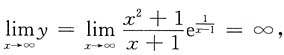
所以曲线
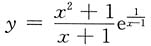
无水平渐近线;由
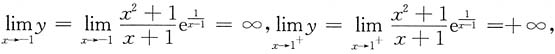
得曲线有两条铅直渐近线;
由
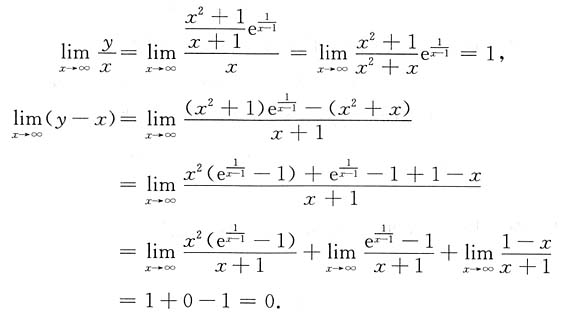
得曲线有一条斜渐近线y=x.
综上知,曲线共有3条渐近线.
2. 设X
1,X
2,…,X
8和Y
1,Y
2,…,Y
10分别是来自正态总体N(-1,4)和N(2,5)的简单随机样本,且相互独立,
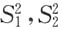
分别为这两个样本的方差,则服从F(7,9)分布的统计量是______
A.
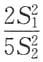
B.
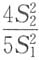
C.
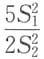
D.
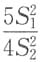
A B C D
D
[解析] 由
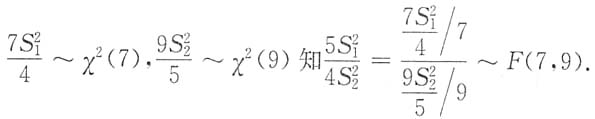
因此本题选(D).
3. 设连续型随机变量X的分布函数为F(x),密度函数为f(x),而且X与-X有相同的分布函数,则______
- A.F(x)=F(-x).
- B.F(x)=-F(-x).
- C.f(x)=f(-x).
- D.f(x)=-f(-x).
A B C D
C
[解析] 利用分布函数的性质F(+∞)=1,F(-∞)=0即可排除选项A和B,由
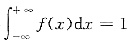
即可排除选项D,所以正确答案为选项C.选项C的正确性可证明如下
F
-X(x)=P{-X≤x}=P{X≥-x}=1-P{X≤-x}=1-F
X(-x),
由已知得
1-F
X(-x)=F
X(x),
两边对x求导,得
f(-x)=f(x).
6. 若α
1=(-1,1,a,4)
T,α
2=(-2,1,5,a)
T,α
3=(A,2,10,1)
T是齐次方程组Ax=0的基础解系,则a的取值为______
- A.a≠5
- B.a≠-4
- C.a≠-3
- D.a≠-3且a≠4
A B C D
A
[解析] α
1,α
2,α
3是基础解系,则α
1,α
2,α
3线性无关,由
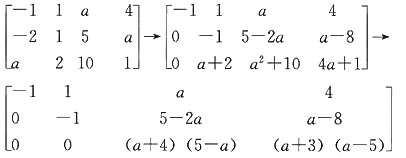
知a≠5.
8. 设n维行向量
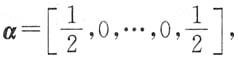
矩阵A=E-α
Tα,B=E+2α
Tα,则AB=______
A B C D
C
[解析] AB=(E-α
Tα)(E+2α
Tα)=E+α
Tα-2α
Tαα
Tα=E+α
Tα-2α
T(αα
T)α.
其中
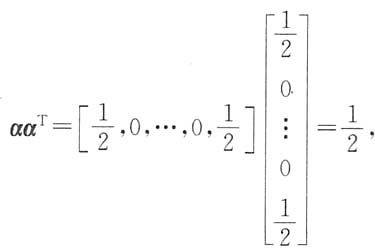
故
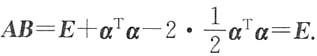
二、填空题1. 三次独立试验中A发生的概率不变,若A至少发生一次的概率为
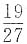
,则一次试验中A发生的概率为______.
[解析] 设一次试验中A发生的概率为p,B={三次试验中A至少发生一次},
则
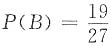
,又P(B)=
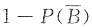
=1-(1-p)
3,
所以有1-(1-p)
3=
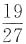
,解得
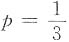
,即一次试验中A发生的概率为
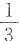
.
2. 设A,B为三阶矩阵,且A的三个特征值为1,2,3,则矩阵
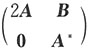
的特征值为______.
2,4,6,6,3,2
[解析]
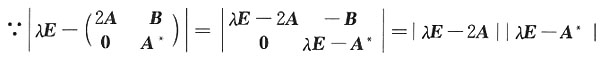
∴只需分别求出2A,A*的特征值即可.设λ为A的特征值,则有Ax=λx,x≠0,于是2Ax=2λx,
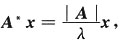
即2A,A*分别有特征值2λ,
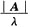
,由题设λ
1=1,λ
2=2,λ
3=3,且|A|=λ
1λ
2λ
3=6,故所求特征值为2,4,6,6,3,2.
本题考查特征值的求法.
3. 设随机变量X和Y独立同分布,且
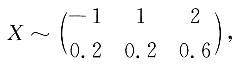
令Z=max{X
2,Y
2},则EZ=______.
3.52
[解析] 本题是求两个离散型随机变量函数的最值分布,一般的方法是先求出随机变量函数的分布,再求最值分布.
由于X和Y相互独立并且服从同一分布,可推出X
2和Y
2也相互独立并且服从同一分布,
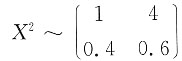
,
则(X
2,Y
2)的联合分布列为
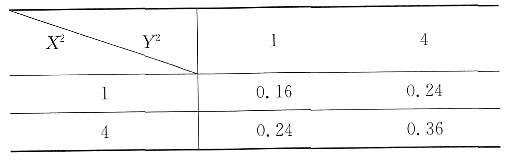
由此得
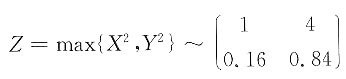
,所以EZ=3.52.
4. 微分方程y'tanx=ylny的通解是______.
y=eCsinx,其中C为任意常数
[解析] 原方程分离变量,有
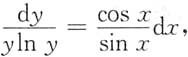
积分得
ln(lny)=ln(sinx)+lnC,通解为lny=Csinx,或y=e
Csinx,其中C为任意常数.
5. 已知函数f(x)=e
sinx+e
-sinx,则f
(2023)(2π)=______.
0
[考点] 初等函数求高阶导数.
[解析] 周期函数和奇偶函数的高阶导数的性质.
因为f(-x)=esin(-x)+e-sin(-x)=e-sinx+esinx=f(x),所以f(x)为偶函数,f(x±2π)=esin(x±2π)+e-sin(x±2π)=esinx+e-sinx=f(x),故f(x)是以T=2π为周期的周期函数.
又偶函数的导函数为奇函数,故f'(x)为奇函数,f"(x)为偶函数,由归纳法易知f(2023)(x)为奇函数.f(x)是以T=2π为周期的周期函数,其导函数也是以T=2π为周期的周期函数,f(2023)(x)也是以T=2π为周期的奇函数.从而f(2023)(2π)=f(2023)(0)=0.故应填0.
另外,要熟记以下结论:
(1)可导的偶函数的导函数为奇函数,可导的奇函数的导函数为偶函数;
(2)偶函数与奇函数的复合函数为偶函数.
6. 设生产某产品平均成本为
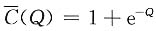
,Q的产量,则边际成本为______.
1+(1-Q)e-Q
[解析] 平均成本为
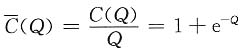
,总成本为C(Q)=Q+Qe
-Q.
边际成本为C'(Q)=1+(1-Q)e
-Q.
三、解答题(共70分.解答应写出文字说明、证明过程或演算步骤.)验收成箱包装的玻璃器皿,每箱24只装.统计资料表明,每箱最多有2只残品,且含0,1,2件残品的箱各占80%,15%,5%.现在随意抽取一箱,随意检验其中4只;若未发现残品则通过验收,否则要逐一检验并更换.试求1. 一次通过验收的概率;
解:设A
i={抽取的一箱中含有i件次品}(i=0,1,2),则A
0,A
1,A
2构成完备事件组,且P(A
0)=0.8,P(A
1)=0.15,P(A
2)=0.05.设B={一次通过验收},则
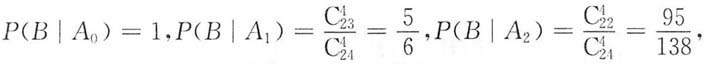
由全概率公式得
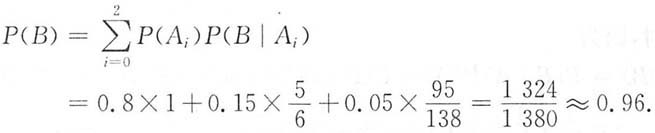
2. 通过验收的箱中确实无残品的概率.
解:由贝叶斯公式得
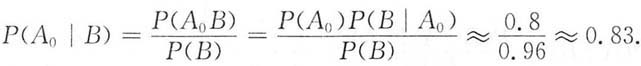
3. 设f(x)在[a,b]上连续且单调减少.证明:当0<k<1时,
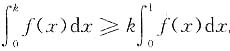
.
证明:方法一
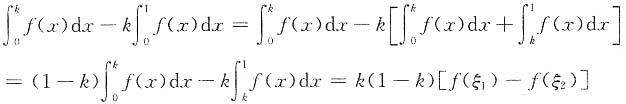
其中ξ
1∈[0,k],ξ
2∈[k,1].因为0<k<1且f(x)单调减少,
所以
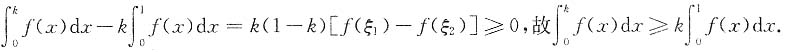
方法二
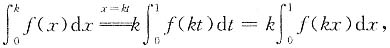
当x∈[0,1]时,因为0<k<1,所以kx≤x,
又因为f(x)单调减少,所以f(kx)≥f(x),两边积分得
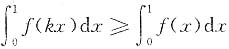
,
故
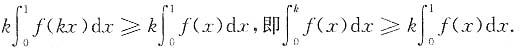
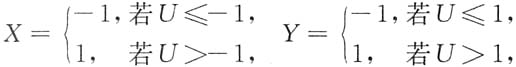
求:4. Cov(X,Y),并判定X与Y的独立性;
解:X,Y的全部可能取值都为-1,1,且
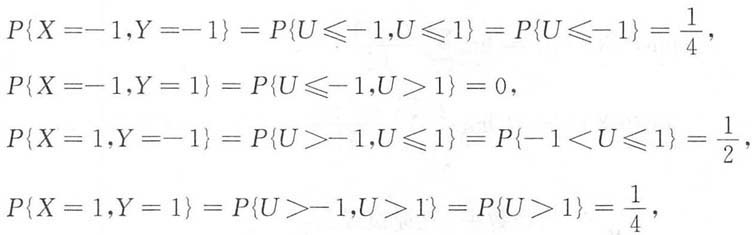
所以(X,Y)的分布律及边缘分布律为
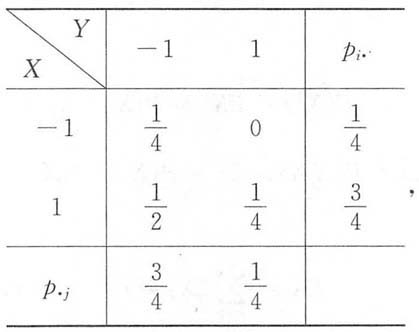
从而
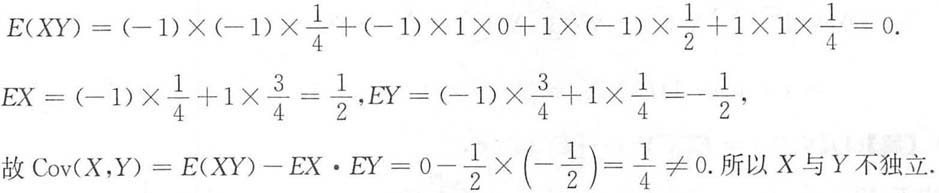
5. D[X(1+Y)].
解:D[X(1+Y)]=D(X+XY)=DX+D(XY)+2Cov(X,XY)
=DX+D(XY)+2E(X
2Y)-2EXE(XY). ①
其中
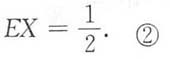
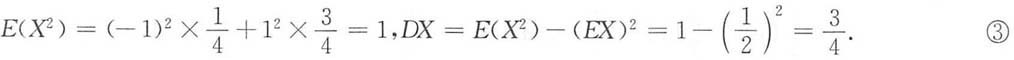
此外,由于XY及X
2Y的分布律分别为
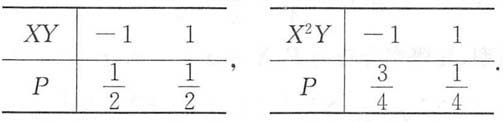
所以
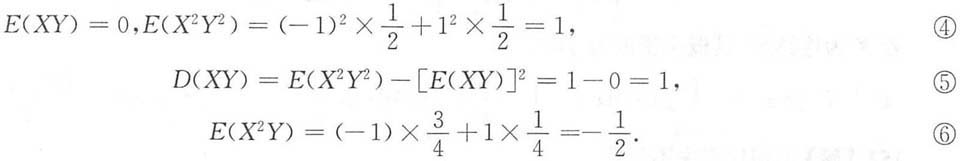
将②~⑥代入①得
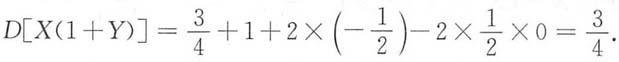
6. 设

试证明:P(A)+P(B)-P(C)≤1.
证:因为

所以
P(C)≥P(AB)=P(A)+P(B)-P(A∪B)≥P(A)+P(B)-1,
故
P(A)+P(B)-P(C)≤1.
7. 证明:方阵A与所有同阶对角阵可交换的充分必要条件是A是对角阵.
证:充分性 A是对角阵,则显然A可与任何对角阵可交换.
必要性 设
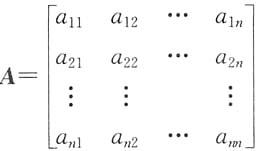
与任何对角阵可交换,则应与对角元素互不相同的对角阵
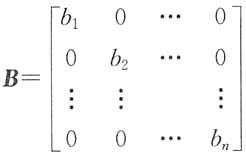
可交换,即

b
1a
12=b
2a
12,b
1≠b
2,故a
12=0.b
ia
ij=b
ja
ij,i≠j,b
i≠b
j,a
ij=0,i=1,2,…,n,j=1,2,…,n,故

是对角阵.
8. 计算
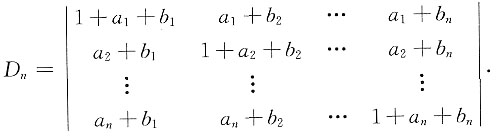
解:依行列式的性质,采用加边法,将行列式升阶为n+1阶行列式,有

利用加边法,将行列式升阶为n+2阶行列式,依行列式性质,有
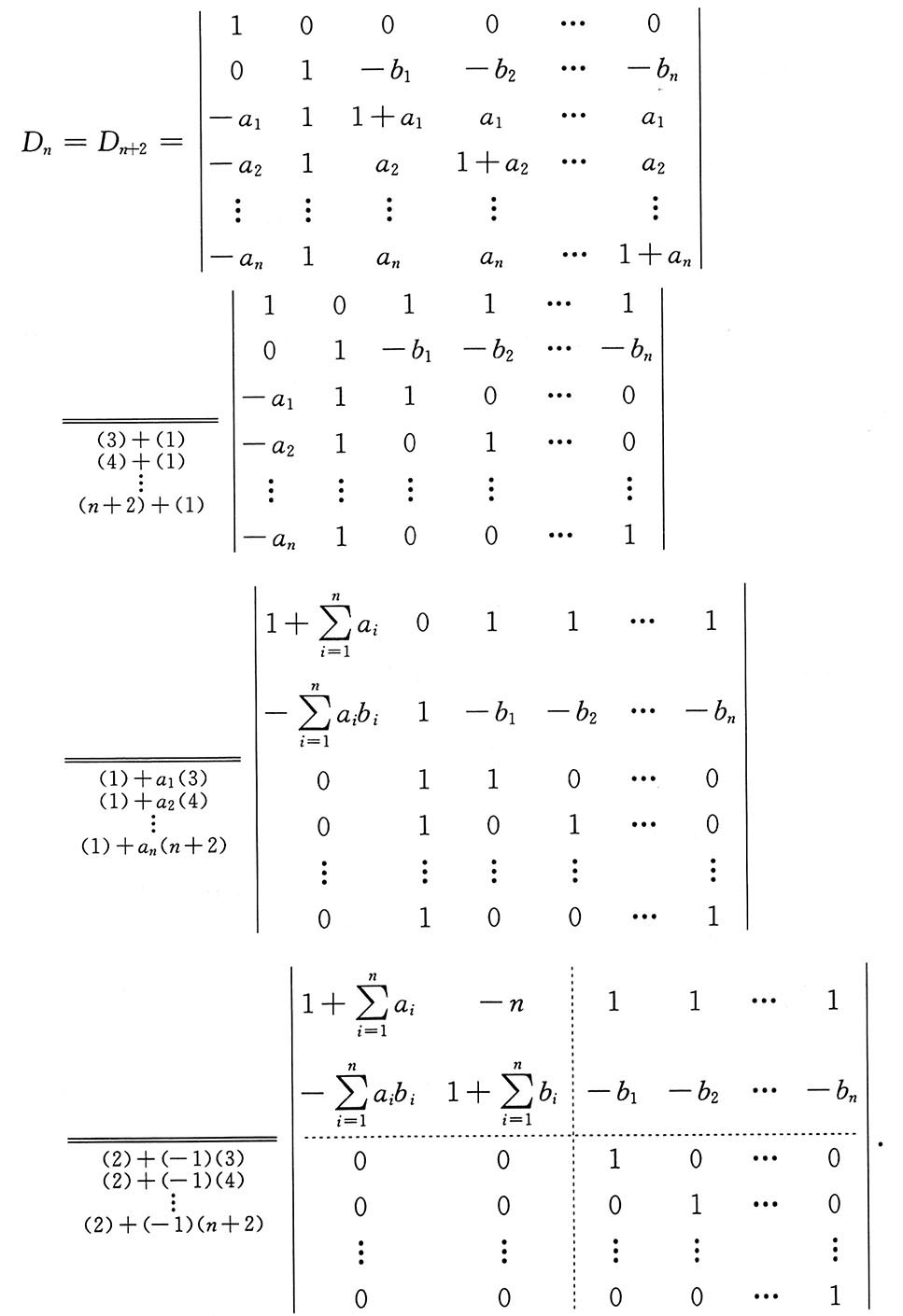
其中,变换在等号上面的表示行变换,在等号下面的表示列变换.
依拉普拉斯定理,得
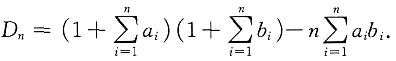
[解析] 与其考虑拆分法,不如尝试加边法,因为拆分的结果未必能简化计算.
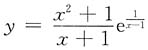 的渐近线的条数为______
的渐近线的条数为______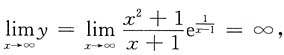 所以曲线
所以曲线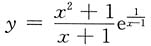 无水平渐近线;由
无水平渐近线;由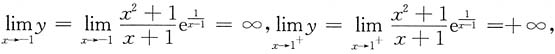 得曲线有两条铅直渐近线;
得曲线有两条铅直渐近线;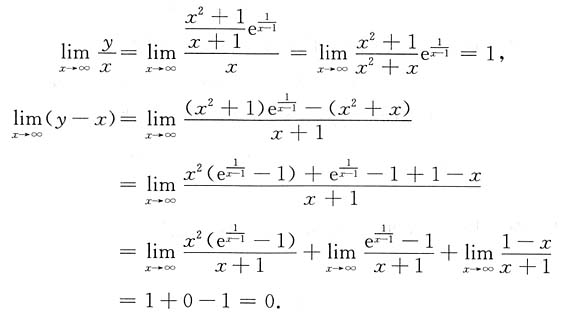
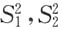 分别为这两个样本的方差,则服从F(7,9)分布的统计量是______
分别为这两个样本的方差,则服从F(7,9)分布的统计量是______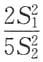
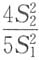
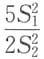
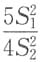
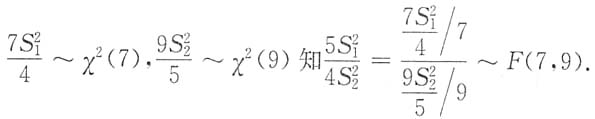 因此本题选(D).
因此本题选(D).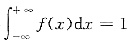 即可排除选项D,所以正确答案为选项C.选项C的正确性可证明如下
即可排除选项D,所以正确答案为选项C.选项C的正确性可证明如下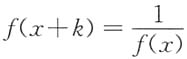 ,则在区间(-∞,+∞)内函数f(x)是______
,则在区间(-∞,+∞)内函数f(x)是______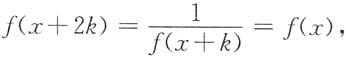 故f(x)是周期函数.
故f(x)是周期函数.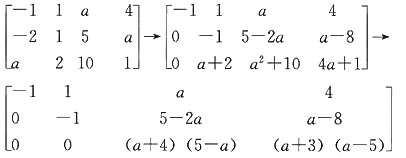
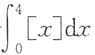 的值为______
的值为______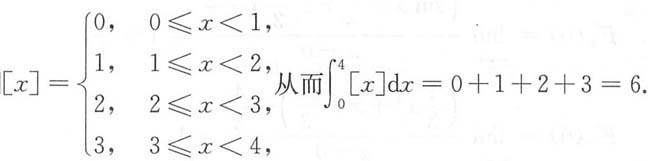
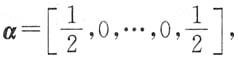 矩阵A=E-αTα,B=E+2αTα,则AB=______
矩阵A=E-αTα,B=E+2αTα,则AB=______
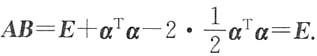
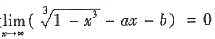 ,则______
,则______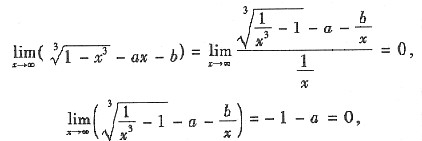
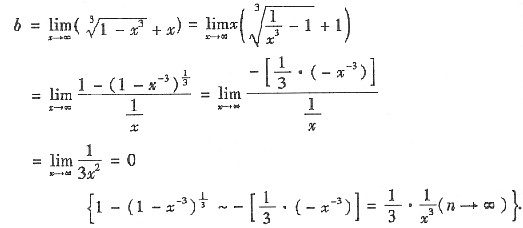
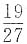 ,则一次试验中A发生的概率为______.
,则一次试验中A发生的概率为______.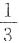
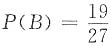 ,又P(B)=
,又P(B)=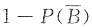 =1-(1-p)3,
=1-(1-p)3,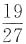 ,解得
,解得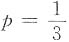 ,即一次试验中A发生的概率为
,即一次试验中A发生的概率为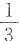 .
.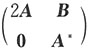 的特征值为______.
的特征值为______.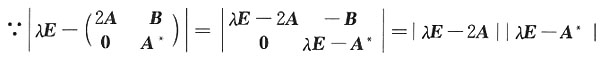 ∴只需分别求出2A,A*的特征值即可.设λ为A的特征值,则有Ax=λx,x≠0,于是2Ax=2λx,
∴只需分别求出2A,A*的特征值即可.设λ为A的特征值,则有Ax=λx,x≠0,于是2Ax=2λx,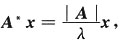 即2A,A*分别有特征值2λ,
即2A,A*分别有特征值2λ,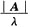 ,由题设λ1=1,λ2=2,λ3=3,且|A|=λ1λ2λ3=6,故所求特征值为2,4,6,6,3,2.
,由题设λ1=1,λ2=2,λ3=3,且|A|=λ1λ2λ3=6,故所求特征值为2,4,6,6,3,2.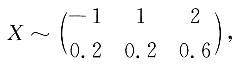
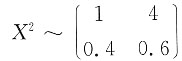 ,
,
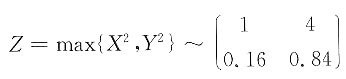 ,所以EZ=3.52.
,所以EZ=3.52.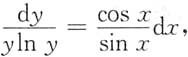 积分得
积分得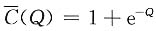 ,Q的产量,则边际成本为______.
,Q的产量,则边际成本为______.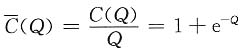 ,总成本为C(Q)=Q+Qe-Q.
,总成本为C(Q)=Q+Qe-Q.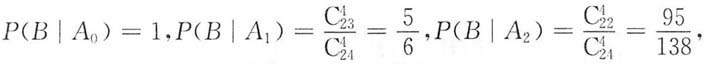
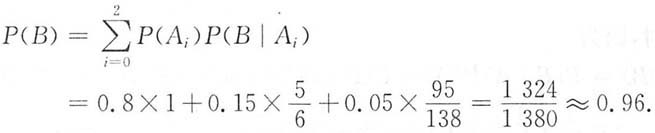
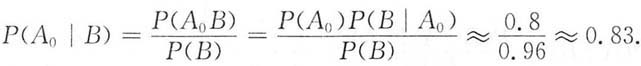
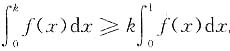 .
.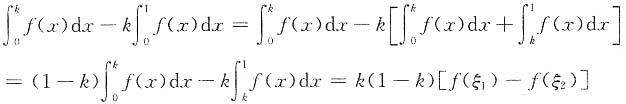
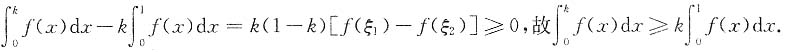
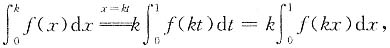 当x∈[0,1]时,因为0<k<1,所以kx≤x,
当x∈[0,1]时,因为0<k<1,所以kx≤x,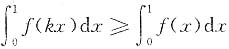 ,
,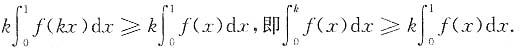
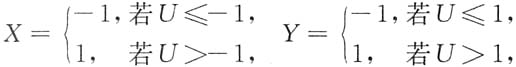
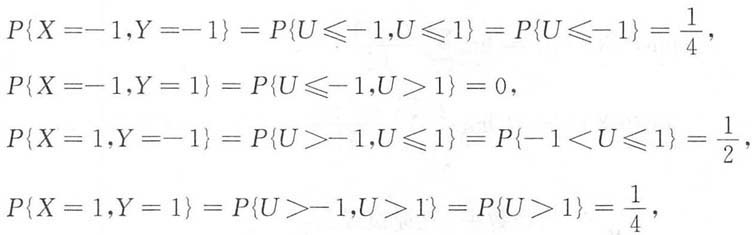

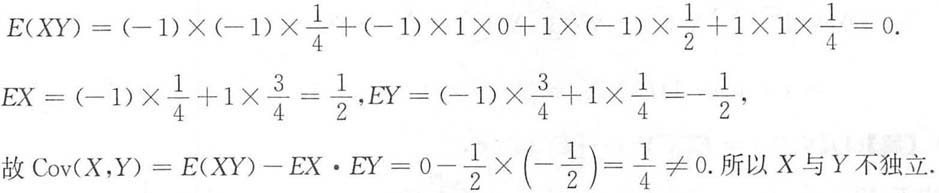
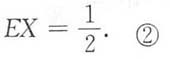
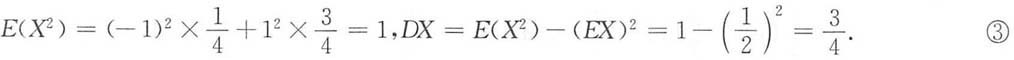
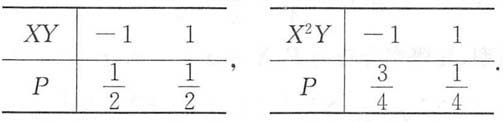
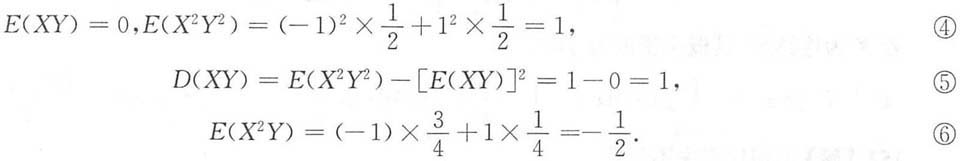
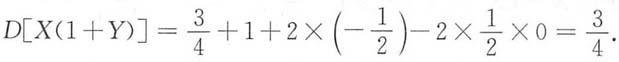
 试证明:P(A)+P(B)-P(C)≤1.
试证明:P(A)+P(B)-P(C)≤1. 所以
所以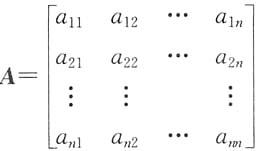 与任何对角阵可交换,则应与对角元素互不相同的对角阵
与任何对角阵可交换,则应与对角元素互不相同的对角阵 可交换,即
可交换,即
 是对角阵.
是对角阵.