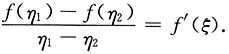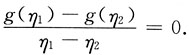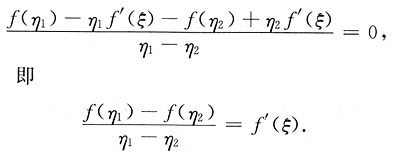一、选择题(下列每题给出的四个选项中,只有一个选项是符合题目要求的.)1. 设函数f(u,v)满足

,则
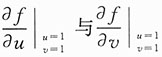
依次是______.
A.

B.

C.
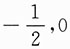
D.
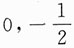
A B C D
D
[考点] 多元复合函数的求导法则.
[解析] 本题可通过分别求

列方程组,从而解出

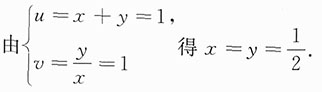
由于
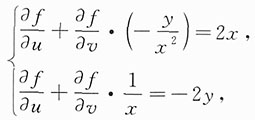
故方程两边关于x,y分别求偏导数得
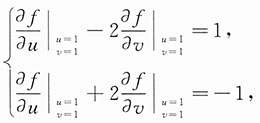
解得
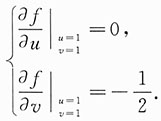
故选D.
本题的关键在于列出关于

的方程组.
2. 已知
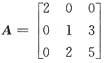
,矩阵B满足A
*B+2A
-1=B,其中A
*是A的伴随矩阵,则|B|=______
A.
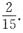
B.
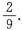
C.
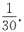
D.
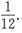
A B C D
A
[解析] 对于矩阵方程首先要恒等变形,左乘A并利用AA
*=A
*A=|A|E,得
|A|B+2E=AB
即(A-|A|E)B=2E
因为|A|=-2,于是(A+2E)B=2E
两边取行列式,得
|A+2E||B|=8
又
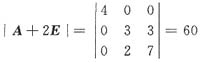
所以
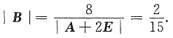
故应选A.
评注:若已知条件是矩阵方程,要先用矩阵运算法则将其化简.
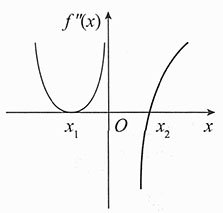
3. 设函数f(x)在(-∞,+∞)内连续,其二阶导函数f"(x)的图形如图所示,则曲线y=f(x)的拐点个数为______.
A B C D
C
[考点] 判定函数的拐点.
[解析] 根据二阶导函数的图像来判定可能的拐点.
由函数的二阶导数图像知:
(1)f"(x
1)=0,当x<x
1及x
1<x<0时,f"(x)>0,所以(x
1,f(x
1))不是拐点.
(2)f"(0)不存在,当0<x<x
2时,f"(x)<0;当x
1<x<0时,f"(x)>0,所以(0,f(0))是拐点.
(3)f"(x
2)=0,当0<x<x
2时,f"(x)<0;当x>x
2时,f"(x)>0,所以(x
2,f(x
2))是拐点.
综合(1)(2)(3)知,有2个拐点,故应选C.
若在x=x
0处f"(x
0)=0(或者是f"(x)不存在的点),且当x变动经过x
0时,f"(x)变号,则(x
0,f(x
0))为拐点.
6. 极限
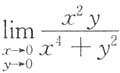
______
A.等于0
B.不存在
C.等于
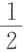
D.存在且不等于0及
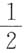
A B C D
B
[解析] 取y=x,则
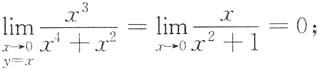
取y=x
2,则
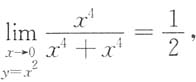
故原极限不存在.
7. 下列命题中正确的是______
A.若u
n<v
n(n=1,2,3,…),则
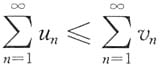
B.若u
n<v
n(n=1,2,3,…),且
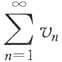
收敛,则
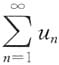
收敛
C.若
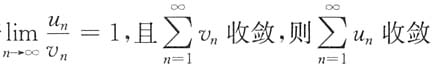
D.若w
n<u
n<v
n(n=1,2,3,…),且

A B C D
D
[解析] 因为w
n<u
n<v
n,所以0<u
n-w
n<v
n-w
n.又因为
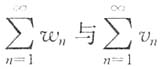
收敛,所以
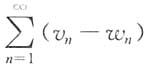
收敛,因而
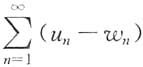
收敛.故
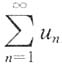
收敛.
因为只有当级数收敛时,才能比较其和的大小,所以不能选A;选项B,C将正项级数的结论用到了一般级数上,显然不对.例如取级数
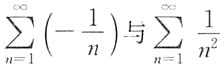
可以说明B不对,取级数

就可以说明C不对.选D.
8. 设a
n>0,n=1,2,…,若
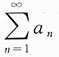
发散,
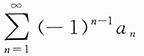
收敛,则下列结论正确的是______.
A.
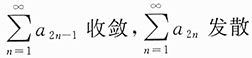
B.
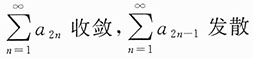
C.
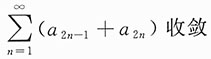
D.
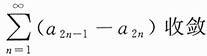
A B C D
D
[考点] 判断常数项级数的收敛性.
[解析] 可通过举反例排除错误的选项,也可通过级数收敛的性质得到正确的选项.
解法1 取
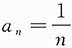
.显然,

都发散,排除A、B.
对于

,因为
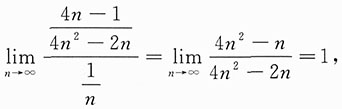
而
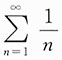
发散,所以
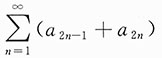
发散,排除C.故选D.
解法2 由性质“若原来的级数收敛,则加括号后所成的级数仍收敛”可知选项D正确.
本题若难以联想到收敛级数的相关性质,则通过举反例亦能排除错误选项.
9. 已知线性非齐次方程组A
3×4x=b(*)有通解k
1(1,2,0,-2)
T+k
2(4,-1,-1,-1)
T+(1,0,-1,1)
T,其中k
1,k
2是任意常数,则满足条件x
1=x
2,x
3=x
4的解是______
- A.(2,2,1,1)T.
- B.(1,1,2,2)T.
- C.(-2,-2,-1,-1)T.
- D.(2,2,-1,-1)T.
A B C D
D
[解析] 方程组(*)的通解足
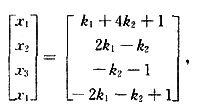
由题意知
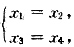
即

解得k
1=1,k
2=0,代入通解.得方程组(*)满足x
1=x
2,x
3=x
4的解是(2,2,-1,-1)
T.故应选D.
10. 设X与Y相互独立,X服从参数为
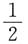
的0—1分布,Y服从参数为
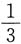
的0—1分布,则方程t
2+2Xt+Y=0中t有相同实根的概率为______
A.
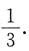
B.

C.
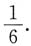
D.
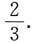
A B C D
B
[解析] 由已知得X与Y的分布为
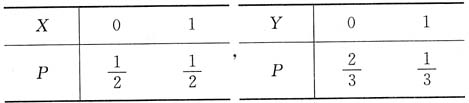
方程中t有相同的实根的概率为
P(4X
2-4Y=0)=P(X
2=Y)
=P(X=0,Y=0)+P(X=1,Y=1)
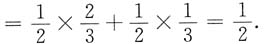
二、填空题1. 若
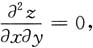
且当x=0时,z=siny;y=0时,z=sinx,则z(x,y)=______.
sinx+siny
[解析]
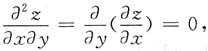
两边对y积分得
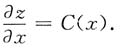
又z(x,0)=sinx,所以
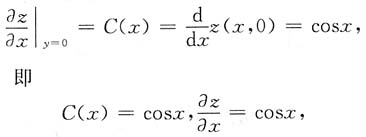
两边对x积分得
z(x,y)=sinx+g(y).
又z(0,y)=g(y)=siny,所以
z(x,y)=sinx+siny.
2. 设
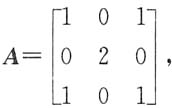
n≥2为正整数,则A
n-2A
n-1=______.
O
[解析]
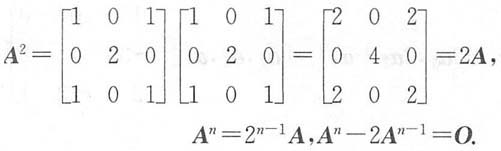
3. 从总体X~N(3.4,6
2)中抽取样本(X
1,X
2,…,X
n),
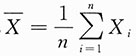
,若
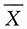
位于(1,4,5,4)内的概率不小于0.95,则样本容量n至少应取______.(已知Φ(1.96)=0.975)
35
[解析] 由X~N(3.4,6
2),知
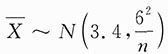
,故
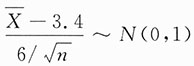
,所以
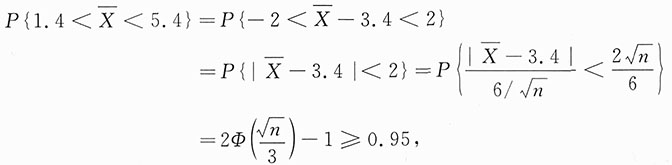
即
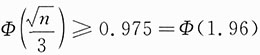
.
由Φ(x)单调增加,知
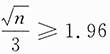
,即n≥(1.96×3)
2≈34.57,所以n至少应取35.
4. 设Y~χ
2(200),则由中心极限定理得P{Y≤200}近似等于______,
[解析] 由Y~χ
2 (200)知,
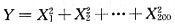
,其中X
1,X
2,…,X
200相互独立且均服从N(0,1).进而知
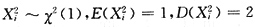
,i=1,2,…,200.由中心极限定理知

5. 设每次试验成功的概率为
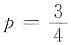
,X表示首次成功需要试验的次数,则X取偶数的概率为______.
[解析] 由P{X=k}=(1-p)
k-1p(k=1,2,…)
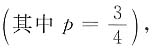
得
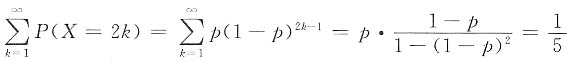
6. 设区域D
t={(x,y)∈R
2|x
2+y
2≤t
2,t>0},函数f(x)在x=0的某邻域内连续且f(0)=A≠0,

若当n→+∞,
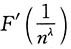
是比
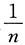
高阶的无穷小量,则参数λ的取值范围是______.
λ>1
[解析] 因为
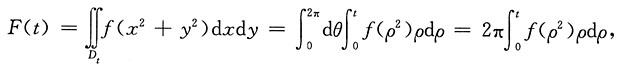
函数ρf(ρ
2)在0的某邻域内连续,所以根据变限定积分函数的性质,可知F(t)在t=0的某邻域内可导,得F'(t)=2πtf(t
2),
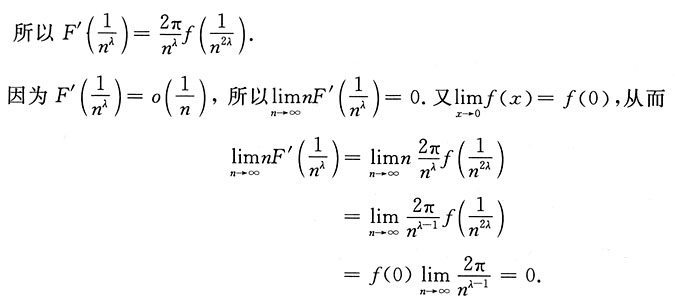
由上式成立可推出,λ>1.
三、解答题(共70分.解答应写出文字说明、证明过程或演算步骤.)1. 已知函数f(u)具有二阶导数,且f'(0)=1,函数y=y(x)由方程y=xe
y-1=1确定.设z=f(lny-sinx),求
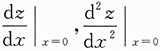
.
解:由方程y-xe
y-1=1得y(0)=1.方程两边对x求导得y'-e
y-1-xe
y-1y'=0,求得y'(0)=1.方程两边再对x求导得y"-2e
y-1y'-x(e
y-1y')'=0,从而得到y"(0)=2.由z=f(lny-sinx)可得
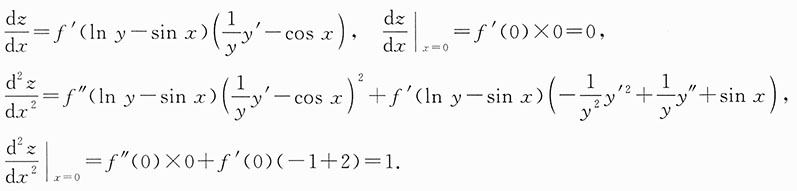
[考点] 复合函数求导.
[解析] 由方程确定的隐函数求导结合复合函数求导法求解.
在进行复合函数求导时,要熟练掌握复合关系,按照链式法则由外及里按顺序求解.
Aα1=α2,Aα2=α3,…,Aαn-1=αn,Aαn=0.2. 证明:α
1,α
2,…,α
n线性无关;
证明:令x
1α
1+x
2α
2+…+r
nα
n=0,则
x
1Aα
1+x
2Aα
2+…+x
nAα
n=0
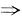
x
1α
2+x
2α
3+…+x
n-1α
n=0
x
1Aα
2+x
2Aα
3+…+x
n-1Aα
n=0
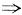
x
1α
3+x
2α
4+…+x
n-22α
n-2=0
…
x
1α
n=0
因为α
n≠0,所以x
1=0,反推可得x
2=…=x
n=0,所以α
1,α
2,…,α
n线性无关.
3. 求A的特征值与特征向量.
解:
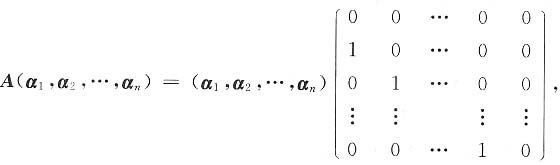
令P=(α
1,α
2,…,α
n),则
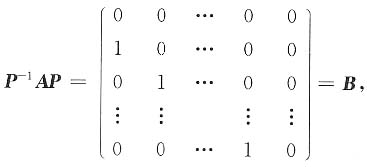
则A与B相似,由|λE=B|=0
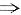
λ
1=…=λ
n=0,即A的特征值全为零,又r(A)=n-1,所以AX=0的基础解系只含有一个线性无关的解向量,而Aα
n=0α
n(α
n≠0),所以A的全部特征向量为kα
n(k≠0).
4. 对于任意正整数n,
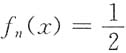
在
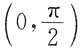
中仅有一根.
证:因为f
n(x)连续,又有f
n(0)=1,
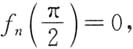
所以由介值定理知
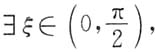
使得
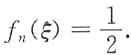
又因为
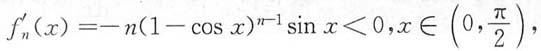
所以f
n(x)在
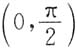
内严格单调减少.因此,满足方程
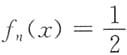
的根ξ是唯一的,即
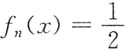
在
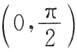
中仅有一根.
5. 设有
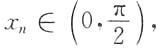
满足
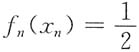
,则
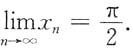
证:因为
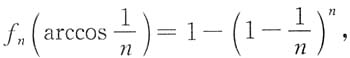
所以
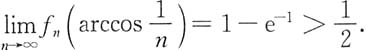
由保号性知,
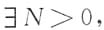
当n>N时,有
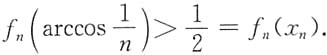
由f
n(x)的单调减少性质知
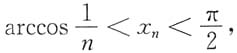
由夹逼准则知
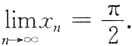
6. 某厂家生产的一种产品同时在两个市场销售,售价分别为p
1和p
2,销售量分别为q
1和q
2.需求函数分别为:q
1=2-ap
1+bp
2,q
2=1-cp
2+dp
1.总成本函数C=3+k(q
1+q
2).其中a,b,c,d,k都为大于0的常数,且4ac≠(b+d)
2.试问厂家如何确定两个市场的售价,能够使获得的总利润最大.
7. 已知函数u(x,y)满足
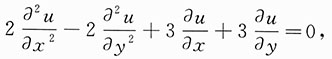
求a,b的值使得在变换u(x,y)=v(x,y)e
ax+by之下,上述等式可化为函数v(x,y)的不含一阶偏导数的等式.
解:
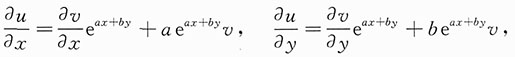
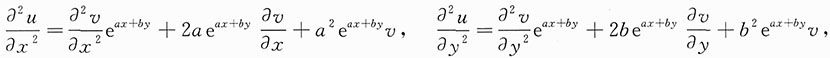
代入
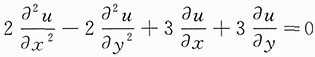
,得
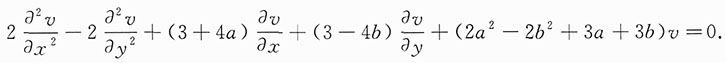
由3+4a=3-4b=0得
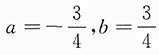
.此时,原等式化为
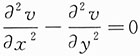
.
[考点] 已知偏导数求参数的值.
[解析] 本题应先根据u(x,y)=v(x,y)e
ax+by分别求出
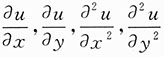
,再将其代入
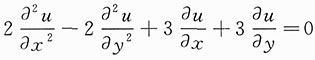
,从而求出a,b的值.
本题计算量较大,在求偏导数时应耐心、细致.
8. 若f'(ξ)=0,则存在x
1,x
2∈(a,b)且x
1<ξ<x
2,使得f(x
1)=f(x
2);
证:因为f"(ξ)>0,f'(ξ)=0,故ξ是f的极小值点.f在[a,ξ]上有最大值f(t1).同样f在[ξ,b]上也存在最大值f(t2).不妨设f(t1)≤f(t2),由连续函数的介值定理可得,存在x0∈[ξ,b],使得f(x0)=f(t1).即有x1=t1,x2=x0使得f(x1)=f(x2).
9. 若f'(ξ)≠0,则存在η
1<ξ<η
2,其中η
1,η
2∈(a,b),使得
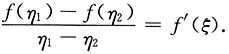
证:由f'(ξ)≠0,令g(x)=f(x)-f'(ξ)x,则g'(ξ)=f'(ξ)-f'(ξ)=0.
于是g(x)符合(Ⅰ)的条件,即存在η
1,η
2∈(a,b)满足η
1<ξ<η
2,使得g(η
1)=g(η
2),即
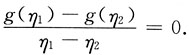
将g(x)=f(x)-f'(ξ)x代入上式后得到
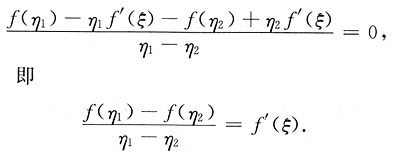
 ,则
,则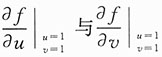 依次是______.
依次是______.

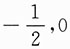
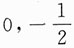
 列方程组,从而解出
列方程组,从而解出
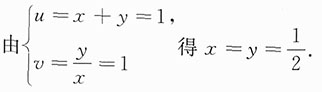
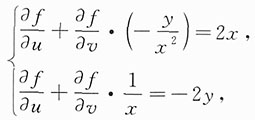
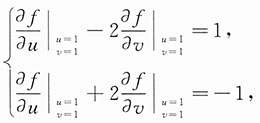
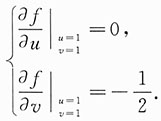
 的方程组.
的方程组.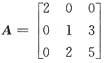 ,矩阵B满足A*B+2A-1=B,其中A*是A的伴随矩阵,则|B|=______
,矩阵B满足A*B+2A-1=B,其中A*是A的伴随矩阵,则|B|=______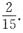
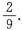
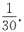
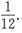
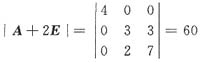
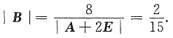 故应选A.
故应选A.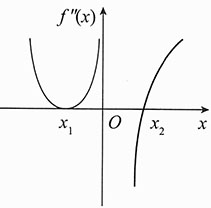
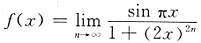 ,则f(x)的间断点______
,则f(x)的间断点______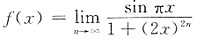
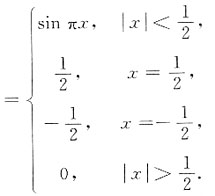
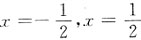 (如下图),选C.
(如下图),选C.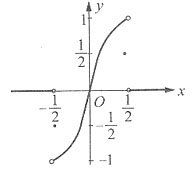
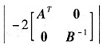 的值为______。
的值为______。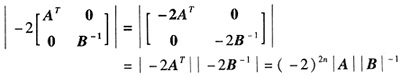 。选D。
。选D。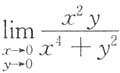 ______
______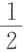
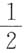
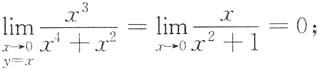 取y=x2,则
取y=x2,则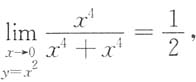 故原极限不存在.
故原极限不存在.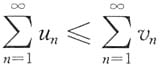
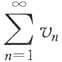 收敛,则
收敛,则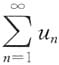 收敛
收敛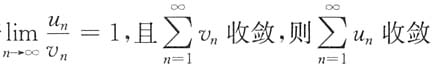

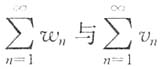 收敛,所以
收敛,所以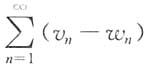 收敛,因而
收敛,因而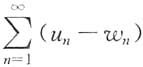 收敛.故
收敛.故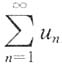 收敛.
收敛.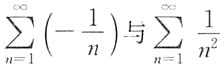 可以说明B不对,取级数
可以说明B不对,取级数 就可以说明C不对.选D.
就可以说明C不对.选D.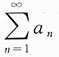 发散,
发散,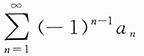 收敛,则下列结论正确的是______.
收敛,则下列结论正确的是______.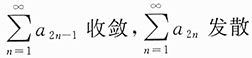
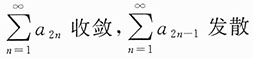
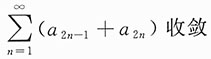
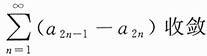
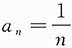 .显然,
.显然, 都发散,排除A、B.
都发散,排除A、B. ,因为
,因为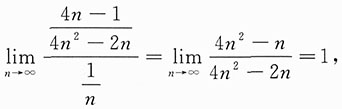
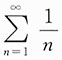 发散,所以
发散,所以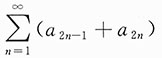 发散,排除C.故选D.
发散,排除C.故选D.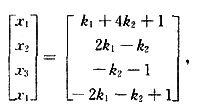
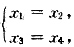 即
即 解得k1=1,k2=0,代入通解.得方程组(*)满足x1=x2,x3=x4的解是(2,2,-1,-1)T.故应选D.
解得k1=1,k2=0,代入通解.得方程组(*)满足x1=x2,x3=x4的解是(2,2,-1,-1)T.故应选D.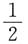 的0—1分布,Y服从参数为
的0—1分布,Y服从参数为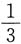 的0—1分布,则方程t2+2Xt+Y=0中t有相同实根的概率为______
的0—1分布,则方程t2+2Xt+Y=0中t有相同实根的概率为______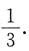

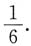
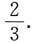
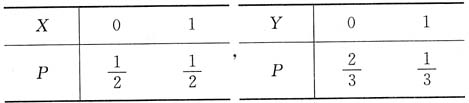
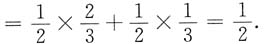
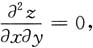 且当x=0时,z=siny;y=0时,z=sinx,则z(x,y)=______.
且当x=0时,z=siny;y=0时,z=sinx,则z(x,y)=______.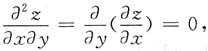 两边对y积分得
两边对y积分得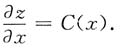 又z(x,0)=sinx,所以
又z(x,0)=sinx,所以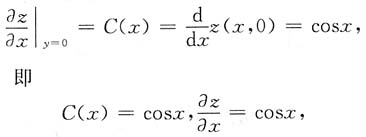
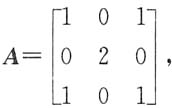 n≥2为正整数,则An-2An-1=______.
n≥2为正整数,则An-2An-1=______.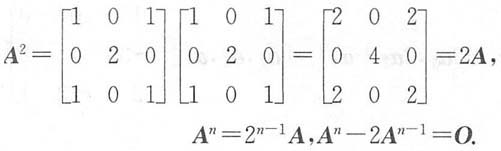
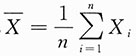 ,若
,若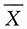 位于(1,4,5,4)内的概率不小于0.95,则样本容量n至少应取______.(已知Φ(1.96)=0.975)
位于(1,4,5,4)内的概率不小于0.95,则样本容量n至少应取______.(已知Φ(1.96)=0.975)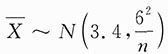 ,故
,故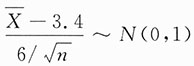 ,所以
,所以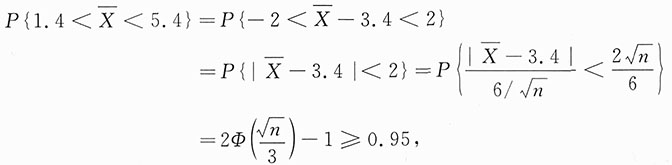
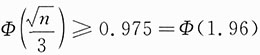 .
.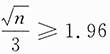 ,即n≥(1.96×3)2≈34.57,所以n至少应取35.
,即n≥(1.96×3)2≈34.57,所以n至少应取35.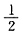
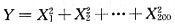 ,其中X1,X2,…,X200相互独立且均服从N(0,1).进而知
,其中X1,X2,…,X200相互独立且均服从N(0,1).进而知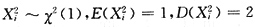 ,i=1,2,…,200.由中心极限定理知
,i=1,2,…,200.由中心极限定理知
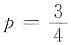 ,X表示首次成功需要试验的次数,则X取偶数的概率为______.
,X表示首次成功需要试验的次数,则X取偶数的概率为______.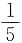
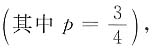 得
得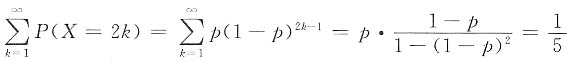
 若当n→+∞,
若当n→+∞,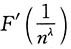 是比
是比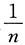 高阶的无穷小量,则参数λ的取值范围是______.
高阶的无穷小量,则参数λ的取值范围是______.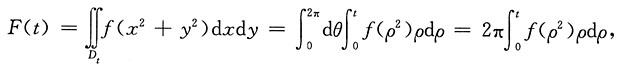 函数ρf(ρ2)在0的某邻域内连续,所以根据变限定积分函数的性质,可知F(t)在t=0的某邻域内可导,得F'(t)=2πtf(t2),
函数ρf(ρ2)在0的某邻域内连续,所以根据变限定积分函数的性质,可知F(t)在t=0的某邻域内可导,得F'(t)=2πtf(t2),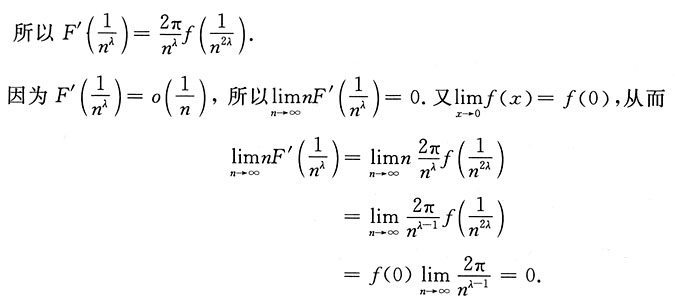
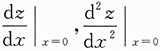 .
.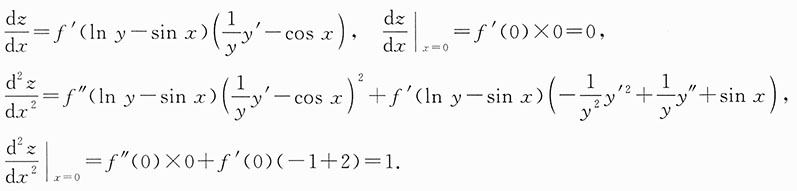
 x1α2+x2α3+…+xn-1αn=0
x1α2+x2α3+…+xn-1αn=0 x1α3+x2α4+…+xn-22αn-2=0
x1α3+x2α4+…+xn-22αn-2=0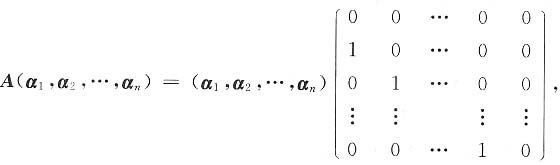 令P=(α1,α2,…,αn),则
令P=(α1,α2,…,αn),则 则A与B相似,由|λE=B|=0
则A与B相似,由|λE=B|=0 λ1=…=λn=0,即A的特征值全为零,又r(A)=n-1,所以AX=0的基础解系只含有一个线性无关的解向量,而Aαn=0αn(αn≠0),所以A的全部特征向量为kαn(k≠0).
λ1=…=λn=0,即A的特征值全为零,又r(A)=n-1,所以AX=0的基础解系只含有一个线性无关的解向量,而Aαn=0αn(αn≠0),所以A的全部特征向量为kαn(k≠0).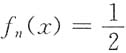 在
在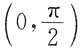 中仅有一根.
中仅有一根.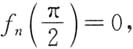 所以由介值定理知
所以由介值定理知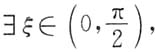 使得
使得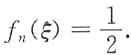 又因为
又因为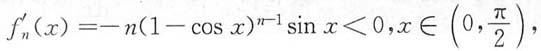 所以fn(x)在
所以fn(x)在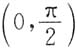 内严格单调减少.因此,满足方程
内严格单调减少.因此,满足方程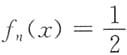 的根ξ是唯一的,即
的根ξ是唯一的,即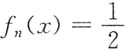 在
在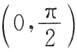 中仅有一根.
中仅有一根.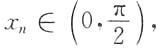 满足
满足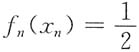 ,则
,则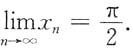
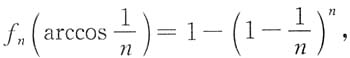 所以
所以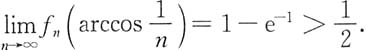
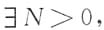 当n>N时,有
当n>N时,有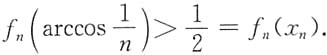
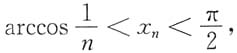 由夹逼准则知
由夹逼准则知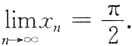
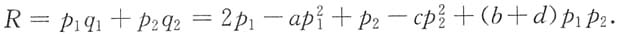
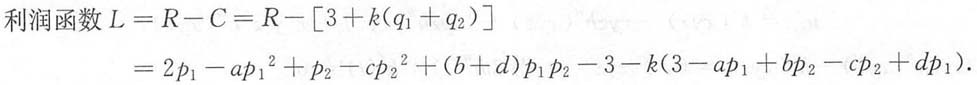
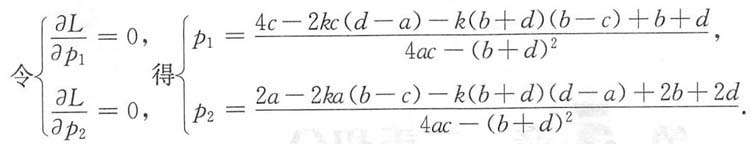
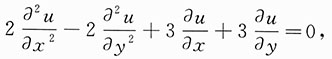
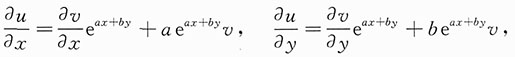
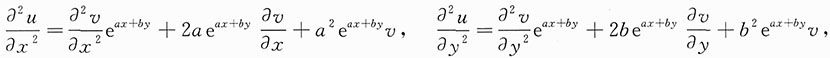
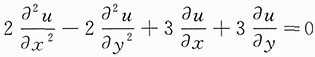 ,得
,得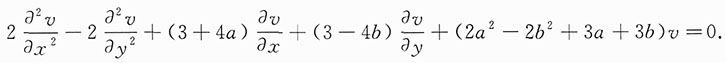
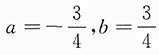 .此时,原等式化为
.此时,原等式化为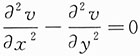 .
.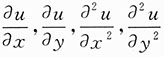 ,再将其代入
,再将其代入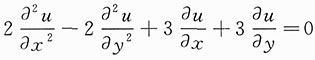 ,从而求出a,b的值.
,从而求出a,b的值.