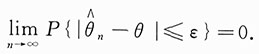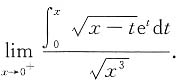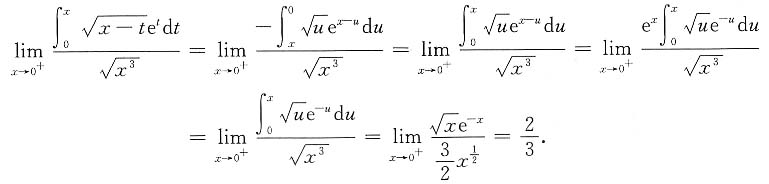一、选择题(下列每题给出的四个选项中,只有一个选项是符合题目要求的.)5. 考虑二元函数f(x,y)的下面4条性质:
①f(x,y)在点(x
0,y
0)处连续;
②f(x,y)在点(x
0,y
0)处的两个偏导数连续;
③f(x,y)在点(x
0,y
0)处可微;
④f(x,y)在点(x
0,y
0)处的两个偏导数存在.若用
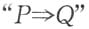
表示可由性质P推出性质Q,则有______
A.
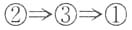
B.
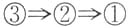
C.
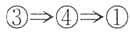
D.

A B C D
A
[解析] 本题考查下图中因果关系的认知:
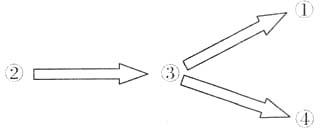
7. 已知α
1,α
2,β
1,β
2均是n维(n≥2)向量,则______
- A.α1,α2线性无关,β1,β2线性无关,必有α1,β1,α2,β2线性无关
- B.α1,α2线性相关,β1,β2线性相关,必有α1,β1,α2,β2线性相关
- C.α1,α2线性无关,β1,β2线性相关,必有α1,β1,α2,β2线性无关
- D.α1,α2线性相关,β1,β2线性无关,则α1,β1,α2,β2可能线性相关,可能线性无关
A B C D
D
[解析] A.例:
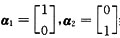
线性无关
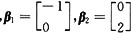
线性无关,但α
1+
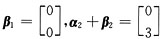
线性相关,A不成立;
B.例:
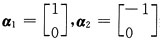
线性相关,
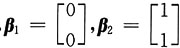
线性相关,但
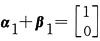
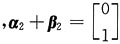
线性无关,B不成立;
C.例:
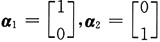
线性相关
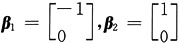
线性相关,但
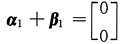
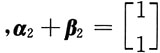
线性相关,C不成立;
由排除法,得D.成立,亦可直接举出两个方面的例子(请读者举例),故选D.
9. 设

,其中a,b,c为实数,则下列选项中,不能使得A
100=E的是______
- A.a=1,b=2,c=-1.
- B.a=1,b=-2,c=-1.
- C.a=-1,b=2,c=-1.
- D.a=-1,b=2,c=1.
A B C D
C
[解析] A为右上三角形矩阵,则A
100仍为右上三角形矩阵,且
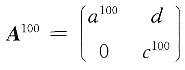
(其中d=a
99b+a
98bc+…+abc
98+bc
99),
若要A
100=E,则a
100=1,c
100=1,d=0,于是a=±1,c=±1,d=0.
当a=c=1时,
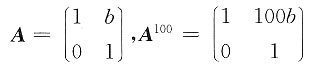
,
若100b=0,即b=0,则A=E,A
100=E,选项中没有此情形;
当a=1,c=-1时,

故A
100=E,b为任意常数,选项A,B均可使得A
100=E;
当a=c=-1时,
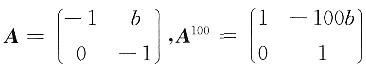
,
若-100b=0,即b=0,则A=-E,A
100=E,故选项C不能使得A
100=E;
当a=-1,c=1时,
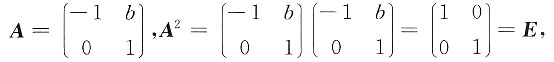
故A
100=E,b为任意常数,选项D可使得A
100=E.选C.
10. 已知y
1=xe
x+e
2x,y
2=xe
x+e
-x是二阶非齐次线性微分方程的解,则此方程为______
- A.y"-y'-2y=ex-2xex.
- B.y"+y'+2y=ex-2xex.
- C.y"-y'-2y=-ex+2xex.
- D.y"+y'+2y=-ex+2xex.
A B C D
A
[解析] y
1-y
2=e
2x-e
-x为对应齐次方程的解.
特征方程为(λ-2)(λ+1)=0,即λ
2-λ-2=0,故对应的齐次方程为y"-y'-2y=0.
代入y
1,有
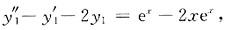
故非齐次方程为y"-y'-2y=e
x-2xe
x,选A.
二、填空题1. 设A,B均为四阶方阵,r(A)=3,r(B)=4,其伴随矩阵分别为A
*,B
*,则r(A
*B
*)=______.
1
[解析] 分别求出r(A*),r(B*).如果r(B*)为满秩矩阵,则r(A*B*)=r(A*).
因r(A)=3,故r(A*)=1(因当r(A)=n-1时,r(A*)=1).又r(B)=4,故r(B*)=4(因r(B)=n,则r(B*)=72),即B*为满秩矩阵,于是
r(A*B*)=r(A*)=1.
2. 设
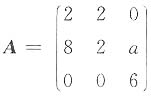
有三个线性无关的特征向量,则a=______.
0
[解析] 由|λE-A|=0得A的特征值为λ1=-2,λ2=λ3=6.因为A有三个线性无关的特征向量,所以A可以对角化,从而r(6E-A)=1,解得a=0.
3. 设X
1,X
2,…,X
100相互独立且在区间[-1,1]上同服从均匀分布,则由中心极限定理
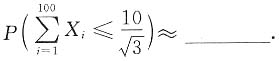
4. 设A,B均是三阶矩阵,其中|A|=2,|B|=-3,则
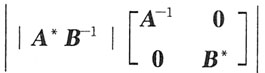
=______.
[解析]
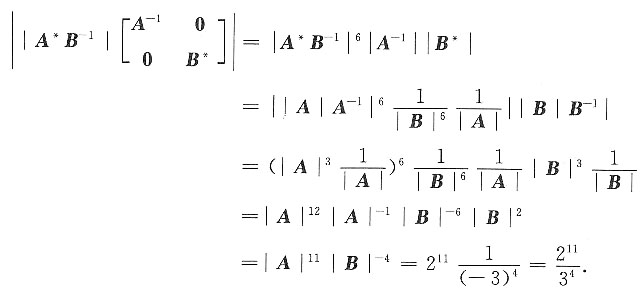
5. 与α
1=[1,2,3,-1]
T,α
2=[0,1,1,2]
T,α
3=[2,1,3,0]
T都正交的单位向量是______.
[解析] 设β=[x
1,x
2,x
3,x
4]
T,那么
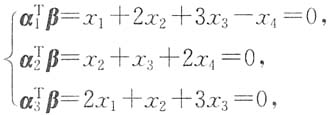
对齐次方程组Ax=0的系数矩阵进行初等行变换,有
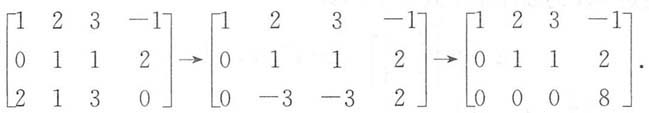
故n-r(A)=4-3=1,则Ax=0有一个基础解向量.则Ax=0的基础解系为[-1,-1.1,0]
T,将其单位化,得
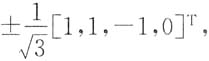
即为所求.
6. 差分方程y
t+1-2y
t=3×2
t的通解为y(t)=______.
[解析] y
t+1-2y
t=0的通解为y(t)=C×2
t,f(t)=3×2
t,因为2为特征值,所以设特解为y
t*=at×2
t,代入原方程得
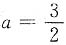
,故原方程的通解
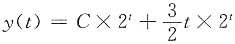
.
三、解答题(共70分.解答应写出文字说明、证明过程或演算步骤.)设随机变量X,Y相互独立,且X的概率分布为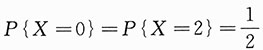 ,Y的概率密度为
,Y的概率密度为 求:
求:1. P{Y≤E(Y)}.
解:
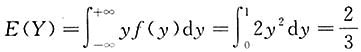
,
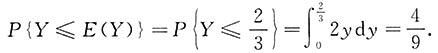
[考点] 考查求概率和二维随机变量函数的分布.
[解析] 先求Y的期望,然后计算相应的概率,最后利用X和Y的分布求Z=X+Y的分布.
2. Z=X+Y的概率密度.
解:Z的分布函数记为F
Z(z),那么
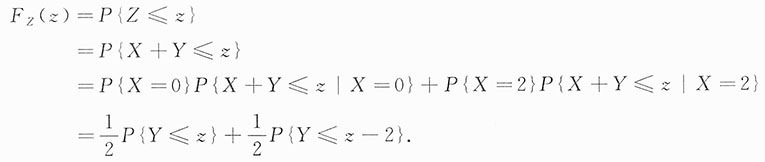
当z<0时,F
Z(z)=0;
当0≤z<1时,

;
当1≤z<2时,
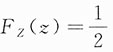
;
当2≤z<3时,
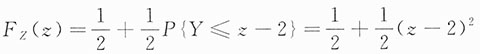
;
当z≤3时,F
Z(z)=1.
所以Z的概率密度为
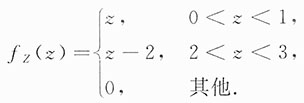
[考点] 考查求概率和二维随机变量函数的分布.
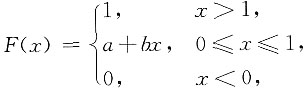
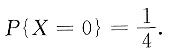
3. 求常数a,b;
解:由于P{X=0}=F(0)-F(0-0)=a-0=a,及
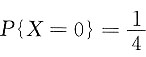
,所以
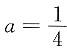
.又F(x)在点x=1处右连续,故F(1+0)=F(1),即1=a+b,解得

进而有
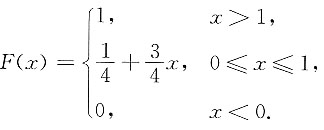
4. 求Y=-lnF(X)的分布函数F
Y(y).
解:因为X在区间[0,1]上取值,所以
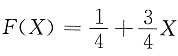
,有
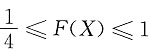
,进而知0≤Y≤ln4.由于
F
Y(y)=P{Y≤y}=P{-lnF(X)≤y}.
当y<0时,
F
Y(y)=P{Y≤y}=0;
当0≤y<ln4时,
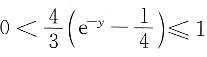
,且F(x)在x>0时连续,故

当y≥ln4时,
F
Y(y)=P{Y≤y}=1.
综上可得
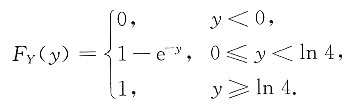
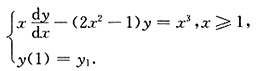
5. 求满足上述微分方程及初始条件的特解;
[解] 改写所给方程为
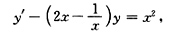
由通解公式得通解
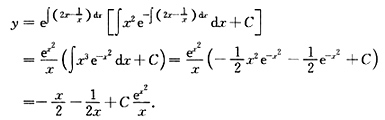
由初始条件y(1)=y
1,得C=(y
1+1)e
-1,得初值问题的特解为
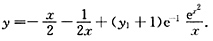
6. 是否存在那种常数y
1,使对应解y=y(x)存在斜渐近线,请求出此y
1及相应的斜渐近线方程.
[解] 若y
1≠-1,则

,无斜渐近线.若y
1=-1,则
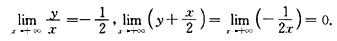
故此时有斜渐近线
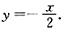
7. 设f(x)在x=0处连续,且x≠0时
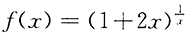
.求曲线y=f(x)在x=0对应的点处的切线方程.
[解] 由f(x)在x=0处连续,所以
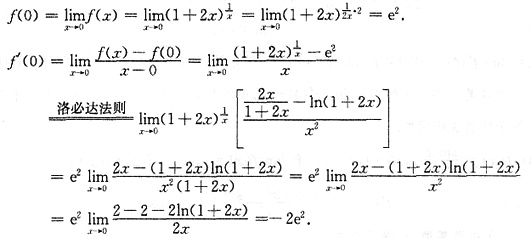
切线方程为y=e
2=-2e
2(x-0),即y=-2e
2x+e
2.
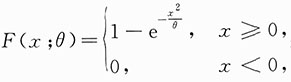 其中θ是未知参数且大于零.X1,X2,…,Xn为来自总体X的简单随机样本.
其中θ是未知参数且大于零.X1,X2,…,Xn为来自总体X的简单随机样本.8. 求E(X)与E(X
2).
[考点] 连续型随机变量的数学期望及参数的点估计.
[解析] 先利用f(x)求出数学期望及未知参数的最大似然估计,然后由大数定律判断a的存在性.
辛钦大数定律:设X
1,X
2,…,X
n,…独立同分布,E(X
i)=μ,则对于
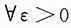
,有

9. 求θ的最大似然估计量
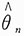
.
解:设x
1,x
2,…,x
n为样本观测值,故似然函数为

当x
1,x
2,…,x
n>0时,
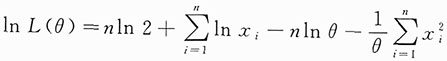
.
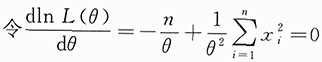
,得θ的最大似然估计值为
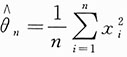
,从而θ的最大似然估计量为
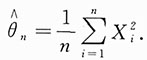
[考点] 连续型随机变量的数学期望及参数的点估计.
10. 问是否存在实数a,使得对任何ε>0,都有
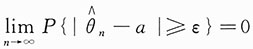
?
解:存在,a=θ.因为
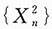
是独立同分布的随机变量序列,且
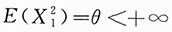
,所以根据辛钦大数定律,当n→∞时,
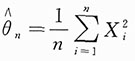
依概率收敛于
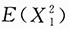
,即θ.所以对任何ε>0都有
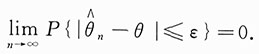
[考点] 连续型随机变量的数学期望及参数的点估计.
11. 求
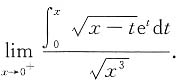
解:令x-t=u,则t=x-u,dt=-du.
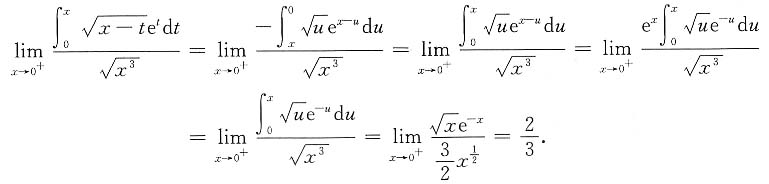
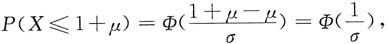 而标准正态分布函数是严格的增函数.
而标准正态分布函数是严格的增函数.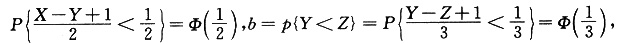
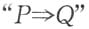 表示可由性质P推出性质Q,则有______
表示可由性质P推出性质Q,则有______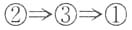



 ,D(Y)=2,故
,D(Y)=2,故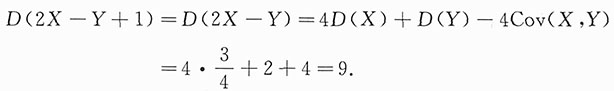
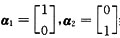 线性无关
线性无关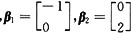 线性无关,但α1+
线性无关,但α1+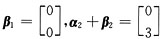 线性相关,A不成立;
线性相关,A不成立;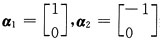 线性相关,
线性相关,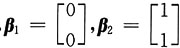 线性相关,但
线性相关,但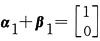
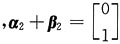 线性无关,B不成立;
线性无关,B不成立;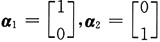 线性相关
线性相关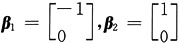 线性相关,但
线性相关,但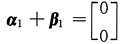
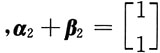 线性相关,C不成立;
线性相关,C不成立;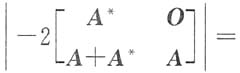 ______
______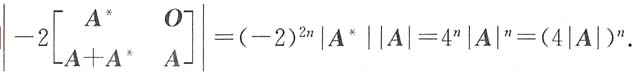
 ,其中a,b,c为实数,则下列选项中,不能使得A100=E的是______
,其中a,b,c为实数,则下列选项中,不能使得A100=E的是______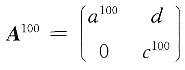 (其中d=a99b+a98bc+…+abc98+bc99),
(其中d=a99b+a98bc+…+abc98+bc99),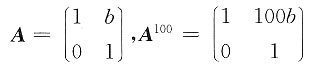 ,
,
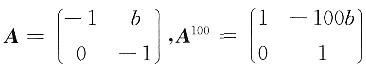 ,
,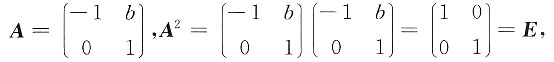
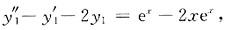 故非齐次方程为y"-y'-2y=ex-2xex,选A.
故非齐次方程为y"-y'-2y=ex-2xex,选A.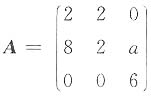 有三个线性无关的特征向量,则a=______.
有三个线性无关的特征向量,则a=______.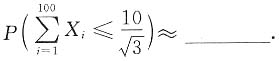
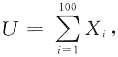 则E(U)=0,D(U)=
则E(U)=0,D(U)=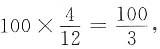
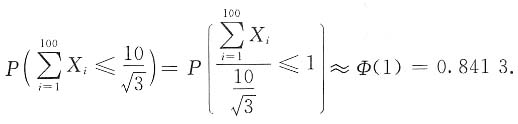
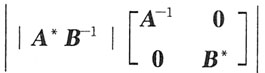 =______.
=______.
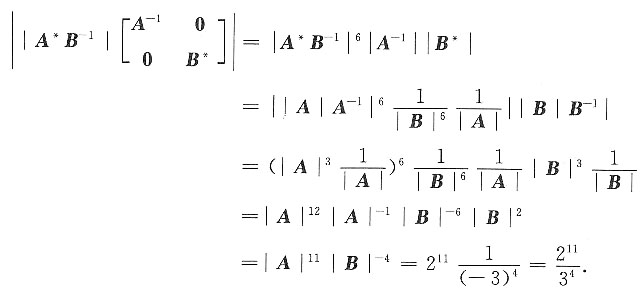
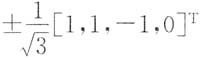
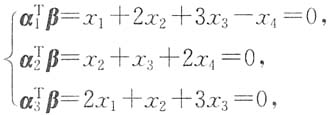
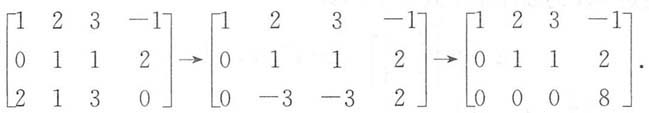
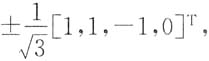 即为所求.
即为所求.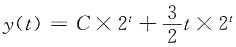
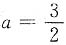 ,故原方程的通解
,故原方程的通解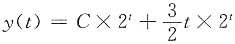 .
.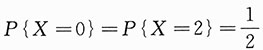 ,Y的概率密度为
,Y的概率密度为 求:
求: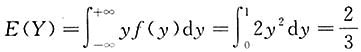 ,
,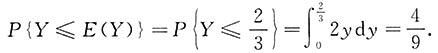
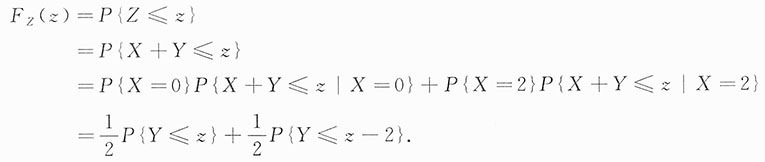
 ;
;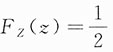 ;
;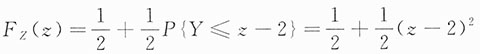 ;
;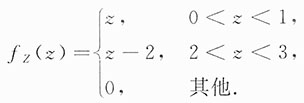
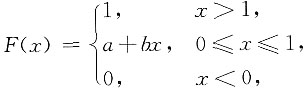
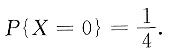
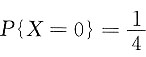 ,所以
,所以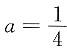 .又F(x)在点x=1处右连续,故F(1+0)=F(1),即1=a+b,解得
.又F(x)在点x=1处右连续,故F(1+0)=F(1),即1=a+b,解得
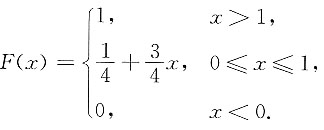
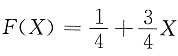 ,有
,有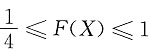 ,进而知0≤Y≤ln4.由于
,进而知0≤Y≤ln4.由于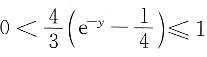 ,且F(x)在x>0时连续,故
,且F(x)在x>0时连续,故
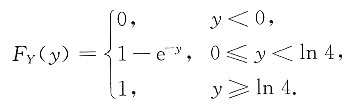
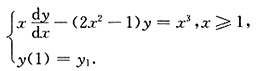
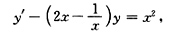
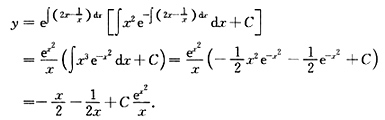
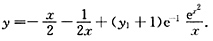
 ,无斜渐近线.若y1=-1,则
,无斜渐近线.若y1=-1,则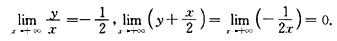
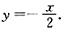
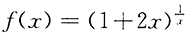 .求曲线y=f(x)在x=0对应的点处的切线方程.
.求曲线y=f(x)在x=0对应的点处的切线方程.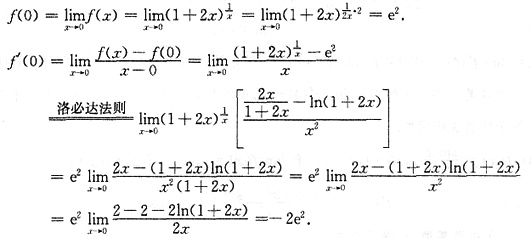
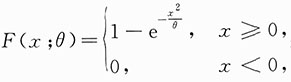 其中θ是未知参数且大于零.X1,X2,…,Xn为来自总体X的简单随机样本.
其中θ是未知参数且大于零.X1,X2,…,Xn为来自总体X的简单随机样本.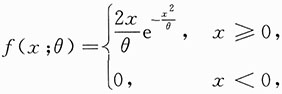 故
故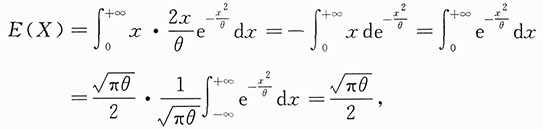
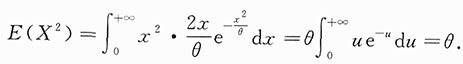
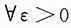 ,有
,有
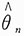 .
.
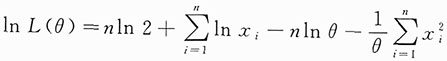 .
.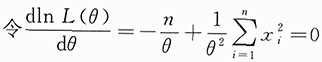 ,得θ的最大似然估计值为
,得θ的最大似然估计值为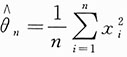 ,从而θ的最大似然估计量为
,从而θ的最大似然估计量为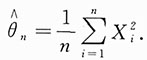
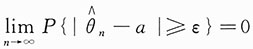 ?
?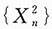 是独立同分布的随机变量序列,且
是独立同分布的随机变量序列,且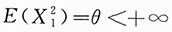 ,所以根据辛钦大数定律,当n→∞时,
,所以根据辛钦大数定律,当n→∞时,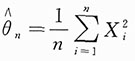 依概率收敛于
依概率收敛于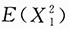 ,即θ.所以对任何ε>0都有
,即θ.所以对任何ε>0都有