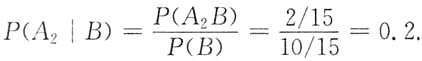一、选择题(下列每题给出的四个选项中,只有一个选项是符合题目要求的.)2. 设A是三阶实对称矩阵,若对任意的三维列向量X,有X
TAX=0,则______.
- A.|A|=0
- B.|A|>0
- C.|A|<0
- D.以上都不对
A B C D
A
[解析] 设二次型
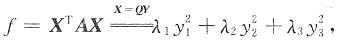
其中Q为正交矩阵.取
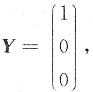
则f=X
TAX=λ
1=0,同理可得λ
2=λ
3=0,由于A是实对称矩阵,所以r(A)=0,从而A=O,选A.
3. 函数
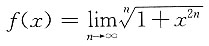
在区间(-∞,+∞)内______
- A.仅有一个不可导的点.
- B.仅有两个不可导的点.
- C.至少有三个不可导的点.
- D.处处可导.
A B C D
B
[解析] 先要将f(x)的具体表达式写出来.
当|x|<1时,

;
当|x|=1时,
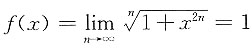
;
当|x|>1时,
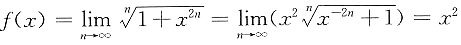
.
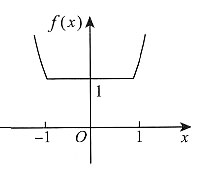
f(x)的图形如图所示,所以f(x)在x=±1处不可导.选B.
5. A是n阶方阵,|A|=3.则|(A
*)
*|=______
- A.3(n-1)2
- B.3n2-1
- C.3n2-n
- D.3n-1
A B C D
A
[解析] |A|=3,A可逆,则
(A
*)(A
*)
*=|A
*|E,
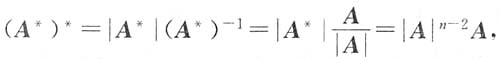
|(A
*)
*|=||A
n-2A|=|A|
(n-2)n|A|=|A|
n2-2n+1=3
(n-1)2.
6. 设m和n为正整数,a>0,且为常数,则下列说法不正确的是______
A.当m为偶数,n为奇数时,
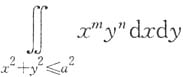
一定为0
B.当m为奇数,n为偶数时,
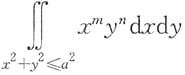
一定为0
C.当m为奇数,n为奇数时,
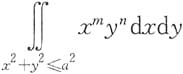
一定为0
D.当m为偶数,n为偶数时,
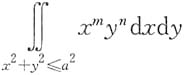
一定为0
A B C D
D
[解析] 令
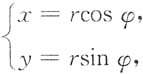
则
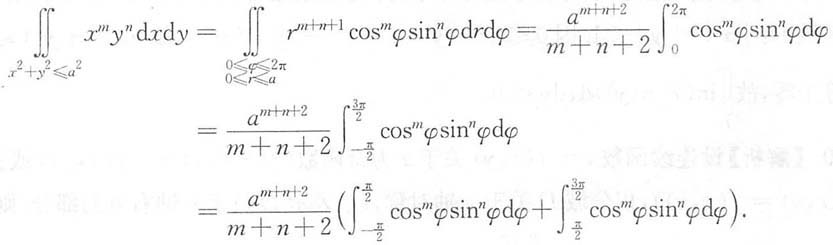
对于
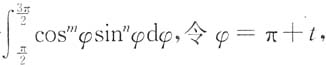
则
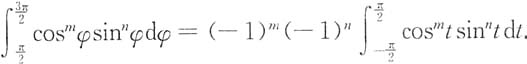
①当m和n中有且仅有一个为奇数时,(-1)
m(-1)
n=-1,从而积分为零;
②当m和n均为奇数时,(-1)
m(-1)
n=1,从而
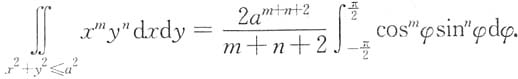
由于
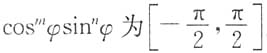
上的奇函数,故积分为零.
总之,当m和n中至少一个为奇数时,
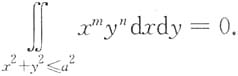
故答案选择(D).
7. 设α
1,α
2,…,α
m与β
1,β
2,…,β
s为两个n维向量组,且r(α
1,α
2,…,α
m)=r(β
1,β
2,…,β
s)=r,则______.
- A.两个向量组等价
- B.r(α1,α2,…,αm,β1,β2,…,βs)=r
- C.若向最组α1,α2,…,αm可由向量组β1,β2,…,βs线性表示,则两向量组等价
- D.两向量组构成的矩阵等价
A B C D
C
[解析] 不妨设向量组α1,α2,…,αm的极大线性无关组为α1,α2,…,αr向量组β1,β2,…,βs的极大线性无关组为β1,β2,…,βr,若α1,α2,…,αm可由β1,β2,…,βs线性表示,则α1,α2,…,αr也可由β1,β2,…,βr线性表示,若β1,β2,…,βr不可由α1,α2,…,αr线性表示,则β1,β2,…,βs也不可由α1,α2,…,αm线性表示,所以两向量组秩不等,矛盾,选C.
9. 设f(x)和φ(x)在(-∞,+∞)内有定义,f(x)为连续函数,且f(x)≠0,φ(x)有间断点,则______.
A.φ[f(x)]必有间断点
B.φ
2(x)必有间断点
C.f[φ(x)]必有间断点
D.
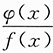
必有间断点
A B C D
D
[考点] 连续函数的运算性质.
[解析] 用反证法及反例排除法求解.
反证法.假设
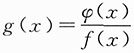
连续,而f(x)连续,由连续函数的运算性质可知,φ(x)=f(x)·g(x)连续,这与φ(x)有间断点矛盾,故

必有间断点,故应选D.
反例排除法.取f(x)=1≠0,
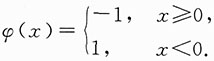
则φ[f(x)]=-1,φ
2(x)=1,f[φ(x)]=1都是连续函数,无间断点,故选项A,B,C错误.
根据连续函数的运算性质,两个连续函数的和、差、积、商(分母非零)仍为连续函数,连续函数与连续函数的复合是连续函数;但是,连续函数与有间断点的函数的复合可能是连续函数,本题中的反例要熟记.
二、填空题1. 将一个骰子重复掷n次,各次掷出的点数依次为X
1,…,X
n则当n→∞时,

依概率收敛于______.
[解析] 题目要求我们计算
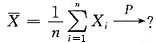
为此我们需要应用大数定律或依概率收敛的定义与性质来计算.由题设知X
1,…,X
n独立同分布:
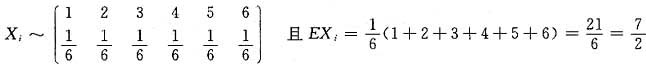
.根据辛钦大数定律:
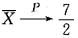
(n→∞).
2. 设u=u(x,y)二阶连续可偏导,且
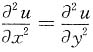
,若u(x,3x)=x,u'
x(x,3x)=x
3,则u"
xy(x,3x)=______.
[解析] u(x,3x)=x两边对x求导,得u'
x(x,3x)+3u'
y(x,3x)=1,
再对x求导,得u"
xx(x,3x)+6u"
xy(x,3x)+9u"
yy(x,3x)=0.
由
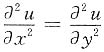
,得10u"
xx(x,3x)+6u"
xy(x,3x)=0,
u'
x(x,3x)=x
3两边对x求导,得u"
xx(x,3x)+3u"
xy(x,3x)=3x
2,
解得
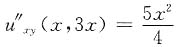
.
3. 已知函数F(x)的导数为
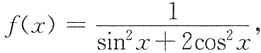
且
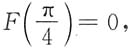
则F(x)=______.
4. 幂级数
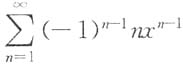
在收敛域(-1,1)内的和函数S(x)为______.
5. 微分方程y"-2y'=x
2+e
2x+1由待定系数法确定的特解形式(不必求出系数)是______.
y*=x(Ax2+Bx+C)+Dxe2x
[解析] 特征方程为r
2-2r=0,特征根r
1=0,r
2=2.
对f
1=x
2+1,λ
1=0是特征根,所以
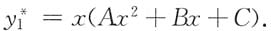
对f
2=e
2x,λ
2=2也是特征根,故有
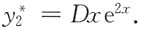
从而y
*如上.
6. 微分方程2x
2y'=(x+y)
2满足定解条件y(1)=1的特解是______。
[考点] 微分方程的特解的求法。
[解析] 题设方程可改写为
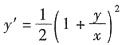
,这是齐次微分方程,令y=xu,则y'=xu'+u代入即得
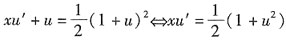
。
分离变量得

从而原方程的通解为
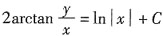
。
它包含定义域分别为x>0与x<0的两族函数:
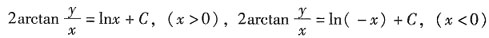
将y(1)=1代入前者有2arctan1=C,即得
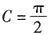
。
故所求的特解为
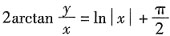
。
三、解答题(共70分.解答应写出文字说明、证明过程或演算步骤.)1. 设A是m×n矩阵,且非齐次线性方程组AX=b满足
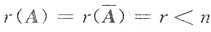
.证明:方程组AX=b的线性无关的解向量的个数最多是n-r+1个.
证:因为r(A)=r<n,所以齐次线性方程组AX=0的基础解系含有n-r个线性无关的解向量,设为ξ1,ξ2,…,ξn-r.
设η0为方程组AX=b的一个特解,
令β0=η0,β1=ξ1+η0,β2=ξ2+η0…,βn-r=ξn-r+η0,显然β0,β1,β2,…,βn-r为方程组AX=b的一组解.
令k0β0+k1β1+…+kn-rβn-r=0,即
(k0+k1+…+kn-r)η0+k1β1+k2β2+…+kn-rβn-r=0,
上式两边左乘A得(k0+k1+…+kn-r)b=0,
因为b为非零列向量,所以k0+k1+…+kn-r=0,于是
k1ξ1+k2ξ2+…+kn-rξn-r=0,
注意到ξ1,ξ2,…,ξn-r线性无关,所以k1=k2=…=kn-r=0,
故β0,ξ1,ξ2,…,ξn-r线性无关,即方程组AX=b存在由n-r+1个线性无关的解向量构成的向量组.设ξ1,ξ2,…,ξn-r+2为方程组AX=b的一组线性无关解,
令γ1=β2-β1,γ2=β3-β1,…,γn-r+1=βn-r+2-β1,根据定义,易证γ1,γ2,…,γn-r+1线性无关,又γ1,γ2,…,γn-r+1为齐次线性方程组AX=0的一组解,即方程组AX=0含有n-r+1个线性无关的解,矛盾,所以AX=b的任意n-r+2个解向量都是线性相关的,所以AX=b的线性无关的解向量的个数最多为n-r+1个.
2. 设可微函数f(x),g(x)满足f'(x)=g(x),g'(x)=f(x),且f(0)=0,g(x)≠0,又设
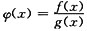
,试导出φ(x)所满足的微分方程,并求φ(x).
3. 某人的食量是2500卡/天,其中1200卡/天用于基本的新陈代谢.在健身运动中,他所消耗的为16卡/千克/天乘以他的体重.假设以脂肪形式储存的热量百分之百有效,而一千克脂肪含热量10000卡,求该人体重怎样随时间变化.
解:输入率为2500卡/天,输出率为(1200+16w),其中w为体重,
根据题意得
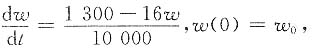
由
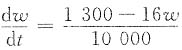
,得
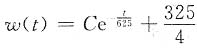
,代入初始条件得
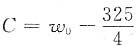
,
于是
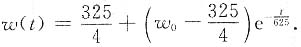
4.
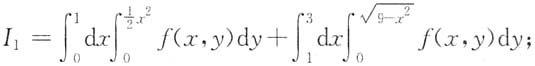
解:由累次积分I的积分限容易写出其对应的二重积分的积分区域σ=σ
1∪σ
2,它们可表示为
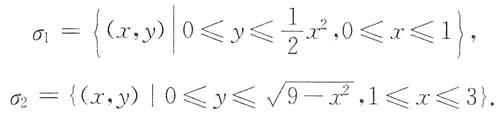
显然,平面区域σ的边界曲线为抛物线
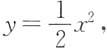
上半圆弧
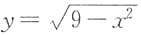
与直线y=0.则σ
1,σ
2也可以写为
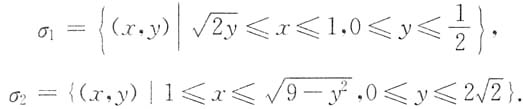
于是,累次积分I交换积分次序后为
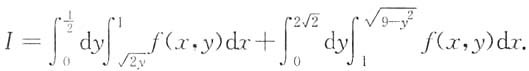
5.
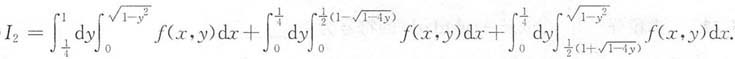
解:由累次积分I的积分限容易写出其对应的二重积分的积分区域为σ=σ
1∪σ
2∪σ
3,其中
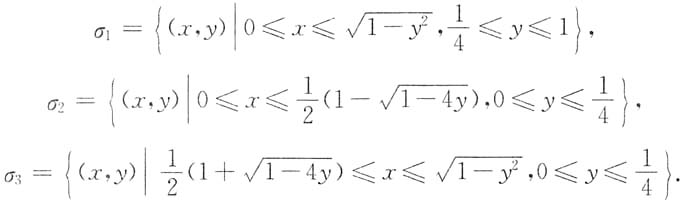
根据区域σ的图形可知,σ的边界曲线是由上半圆
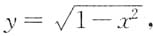
直线x=0与抛物线y=x-x
2组成,故可用不等式表示为
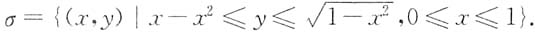
于是,累次积分I化为另一种先对y后对x的累次积分
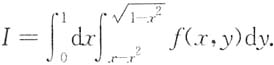
6. 求二元函数z=f(x,y)=x
2y(4-x-y)在由x轴、y轴及x+y=6所围成的闭区域D上的最小值和最大值.
解:(1)求f(x,y)在区域D的边界上的最值,
在L
1:y=0(0≤x≤6)上,z=0;
在L
2:x=0(0≤y≤6)上,z=0;
在L
3:y=6-x(0≤x≤6)上,z=-2x
2(6-x)=2x
3-12x
2,
由
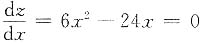
得x=4,因为f(0,0)=0,f(6,0)=0,f(4,2)=-64,所以f(x,y)在L
3上最小值为-64,最大值为0.
(2)在区域D内,由
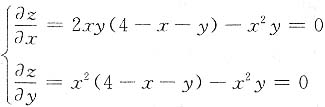
得驻点为(2,1),
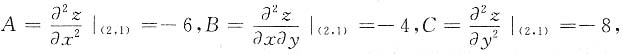
因为AC-B
2>0且A<0,所以(2,1)为f(x,y)的极大点,极大值为f(2,1)=4,
故z=f(x,y)在D上的最小值为m=f(4,2)-64,最大值为M=f(2,1)=4.
7. 设10件产品中有4件不合格品,从中任取两件,已知所取两件中有一件是不合格品,求另一件也是不合格品的概率.
解:设事件A
i={从10件产品中任取两件,有i件不合格品},i=0,1,2.记B=A
1∪A
2,按题意,所求概率为P(A
2|B).而
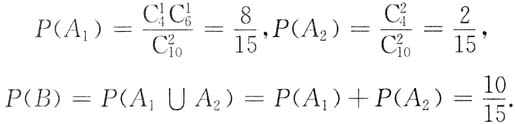
因为

所以P(A
2B)=P(A
2),应用条件概率公式得
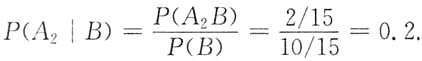
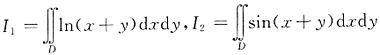 ,其中D由x=0,y=0,x+y=1,x+y=a(0<a<1)围成,侧I1,I2之间的大小关系是______
,其中D由x=0,y=0,x+y=1,x+y=a(0<a<1)围成,侧I1,I2之间的大小关系是______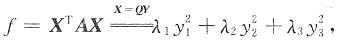 其中Q为正交矩阵.取
其中Q为正交矩阵.取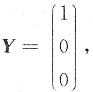 则f=XTAX=λ1=0,同理可得λ2=λ3=0,由于A是实对称矩阵,所以r(A)=0,从而A=O,选A.
则f=XTAX=λ1=0,同理可得λ2=λ3=0,由于A是实对称矩阵,所以r(A)=0,从而A=O,选A.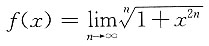 在区间(-∞,+∞)内______
在区间(-∞,+∞)内______ ;
;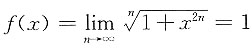 ;
;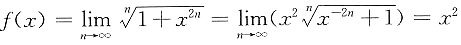 .
.
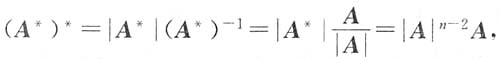
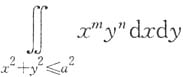 一定为0
一定为0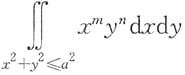 一定为0
一定为0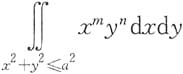 一定为0
一定为0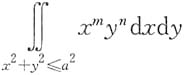 一定为0
一定为0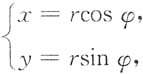 则
则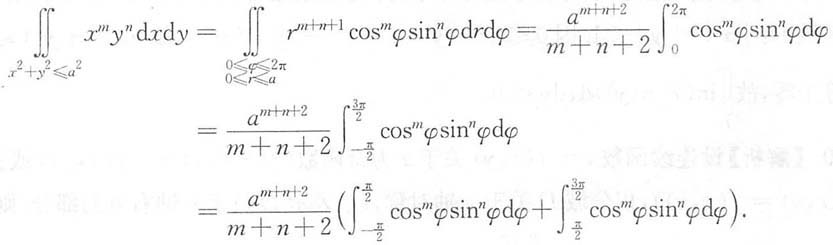
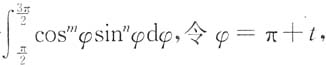 则
则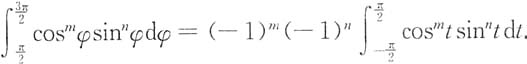
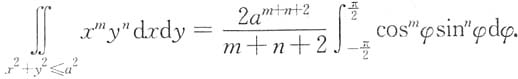
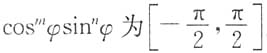 上的奇函数,故积分为零.
上的奇函数,故积分为零.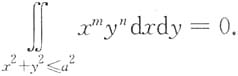 故答案选择(D).
故答案选择(D).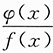 必有间断点
必有间断点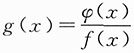 连续,而f(x)连续,由连续函数的运算性质可知,φ(x)=f(x)·g(x)连续,这与φ(x)有间断点矛盾,故
连续,而f(x)连续,由连续函数的运算性质可知,φ(x)=f(x)·g(x)连续,这与φ(x)有间断点矛盾,故 必有间断点,故应选D.
必有间断点,故应选D.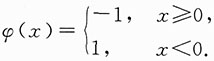 则φ[f(x)]=-1,φ2(x)=1,f[φ(x)]=1都是连续函数,无间断点,故选项A,B,C错误.
则φ[f(x)]=-1,φ2(x)=1,f[φ(x)]=1都是连续函数,无间断点,故选项A,B,C错误. 依概率收敛于______.
依概率收敛于______.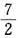
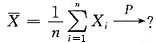 为此我们需要应用大数定律或依概率收敛的定义与性质来计算.由题设知X1,…,Xn独立同分布:
为此我们需要应用大数定律或依概率收敛的定义与性质来计算.由题设知X1,…,Xn独立同分布: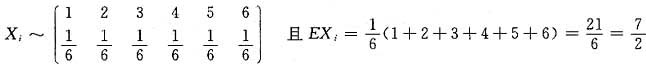 .根据辛钦大数定律:
.根据辛钦大数定律: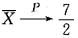 (n→∞).
(n→∞).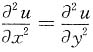 ,若u(x,3x)=x,u'x(x,3x)=x3,则u"xy(x,3x)=______.
,若u(x,3x)=x,u'x(x,3x)=x3,则u"xy(x,3x)=______.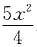
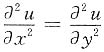 ,得10u"xx(x,3x)+6u"xy(x,3x)=0,
,得10u"xx(x,3x)+6u"xy(x,3x)=0,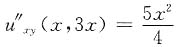 .
.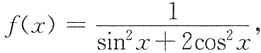 且
且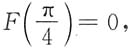 则F(x)=______.
则F(x)=______.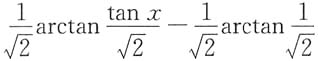
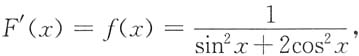 故
故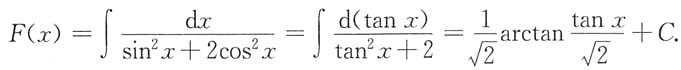
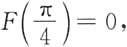 得
得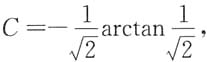 故
故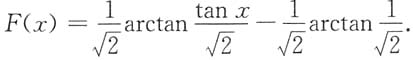
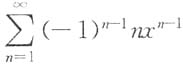 在收敛域(-1,1)内的和函数S(x)为______.
在收敛域(-1,1)内的和函数S(x)为______.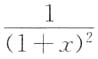
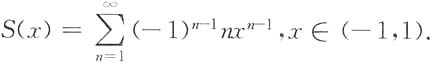
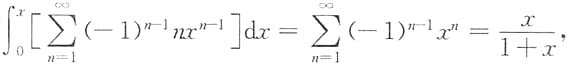 即
即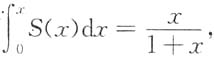 故
故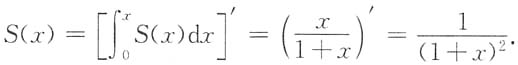
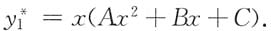
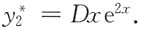 从而y*如上.
从而y*如上.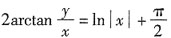
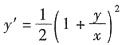 ,这是齐次微分方程,令y=xu,则y'=xu'+u代入即得
,这是齐次微分方程,令y=xu,则y'=xu'+u代入即得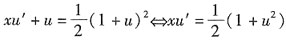 。
。
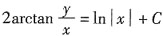 。
。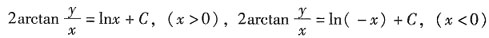
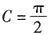 。
。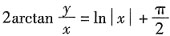 。
。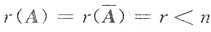 .证明:方程组AX=b的线性无关的解向量的个数最多是n-r+1个.
.证明:方程组AX=b的线性无关的解向量的个数最多是n-r+1个.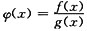 ,试导出φ(x)所满足的微分方程,并求φ(x).
,试导出φ(x)所满足的微分方程,并求φ(x).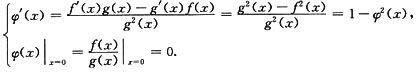

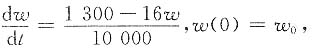
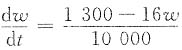 ,得
,得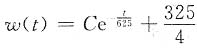 ,代入初始条件得
,代入初始条件得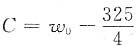 ,
,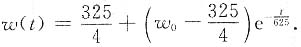
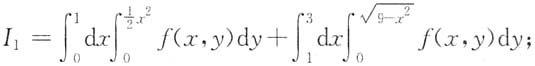
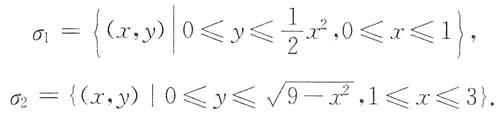
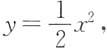 上半圆弧
上半圆弧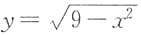 与直线y=0.则σ1,σ2也可以写为
与直线y=0.则σ1,σ2也可以写为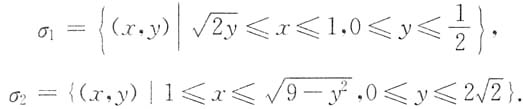
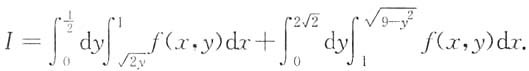
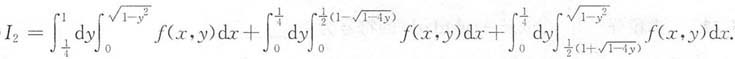
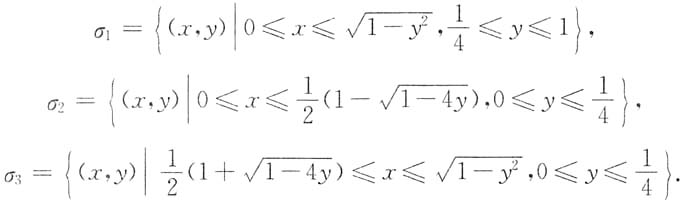
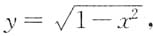 直线x=0与抛物线y=x-x2组成,故可用不等式表示为
直线x=0与抛物线y=x-x2组成,故可用不等式表示为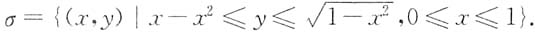
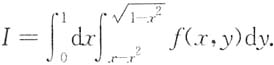
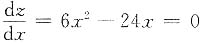 得x=4,因为f(0,0)=0,f(6,0)=0,f(4,2)=-64,所以f(x,y)在L3上最小值为-64,最大值为0.
得x=4,因为f(0,0)=0,f(6,0)=0,f(4,2)=-64,所以f(x,y)在L3上最小值为-64,最大值为0.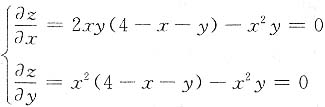 得驻点为(2,1),
得驻点为(2,1),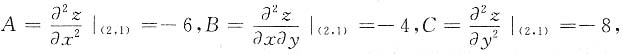
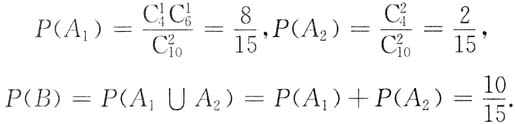
 所以P(A2B)=P(A2),应用条件概率公式得
所以P(A2B)=P(A2),应用条件概率公式得