一、填空题1. 函数y=f(x)和y=g(x)的图形如2-1图所示,则复合函数f[g(x)]在z=1处的导数等于______.
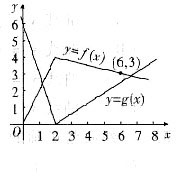
[分析]
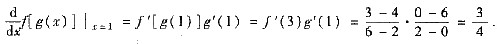
2. 已知直线L过点M(1,-2,0)且与两条直线,
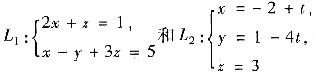
垂直,则L的参数方程为______.
x=1+8t,y=-2+2t,z=-t
[分析] 直线L1的方向向量s1={2,0,1}×{1,-1,3}={1,-5,-2},直线L2的方向向量s2={1,-4,0},于是所求直线的方向向量s={1,-5,-2}×{1,-4,0}=-{8,2,-1},从而所求直线L的参数方程为x=1+8t,y=-2+2t,z=-t.
3.
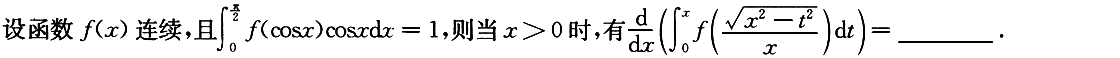
4.

5.

6. 若当x→0时f(x)
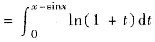
是与x
n同阶的无穷小,则n=______.
6
[分析] 当x→0时,ln(1+x)~x,
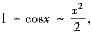
于是
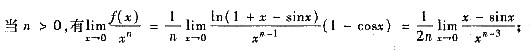
对n>3再用洛必达法则得
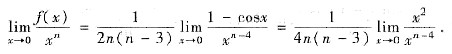
由题设知
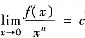
(非零常数),所以n=6.
二、选择题5. 下列命题正确的是
- A.若函数f(x)在(-∞,+∞)内处处可微,则其导函数f'(x)必处处连续.
- B.若函数f(x)在点x0可微,则当△x→0时,△y与dy是同阶无穷小.
- C.设函数y=f(u)二阶可导,则由dy=f'(u)du知
d2y=d[f'(u)du]=[f'(u)du]'du=f"(u)(du)2. - D.若函数f(x)在点x0可导,则f(x)在点x0可微分.
A B C D
D
[分析] 对于(A):例如,函数
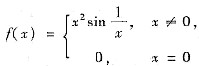
在(-∞,+∞)内处处可微,但f'(x)在点x=0处不连续.故(A)不正确.
对于(B):例如,函数f(x)=x
2在点x
0=0的微分dy=0,它不是△y=(△x)
2当△x→0时的同阶无穷小.故(B)不正确.
[评注] 一般地,若f'(x
0)≠0,则dy=f'(x
0)△x与△y为△x→0时的同阶无穷小.
对于(C):当u为自变量时,结论成立.当u为中间变量时,可设u=φ(x),其中x为自变量,则
d
2y=d(dy)=[f'(u)φ'(x)]'(dx)
2 =[f"(u)φ'(x)φ'(x)+f(u)φ"(x)](dx)
2 =f"(u)(du)
2+f'(u)d
2u.
从而当u为中间变量时函数y=f(u)的二阶微分在形式上就不具有不变性,这就是我们为什么强调一阶微分形式具有不变性的原因.故(C)也不一定正确.
对于(D):由命题“函数f(x)在点x
0可微的充分必要条件是函数f(x)在点x
0可导”可知,(D)正确.
综上分析,应选(D).