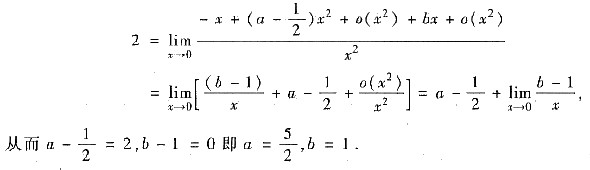一、填空题1.
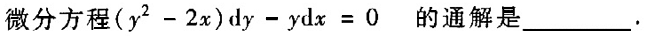
2. 微分方程xy'+2y=xlnx满足
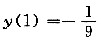
的解为______．
3.
4. 设
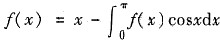
，则f(x)=______．
x+2
[分析] 等式两边都乘以cosx得：
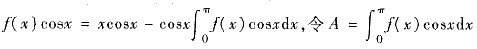
，则
f(x)cosx=xcosx-Acosx，因此
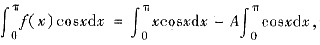
所以A=-2，故f(x)=x+2．
5. 设f'(x)在[-1，1]上连续，则
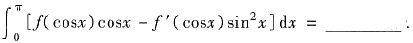
0
[分析]
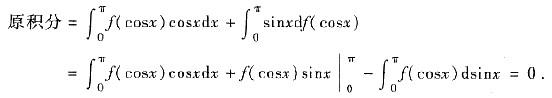
6. 设x→0时，
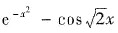
与ax
n是等价无穷小，则a=______，n=______．
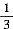
4
[分析一] 用洛必达法则计算极限．由于
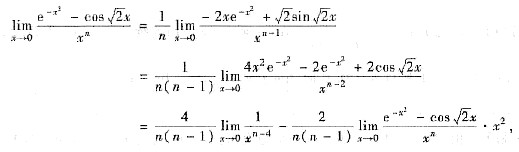
由上式可见，当n=4时有
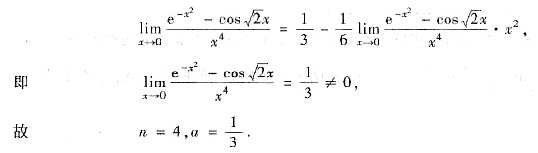
三、解答题1. 设f(x)
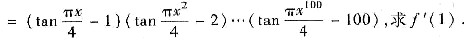
2. 将函数
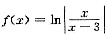
展开成(x-2)的幂级数，并求出其成立范围．
命u=x-2，于是x=u+2，
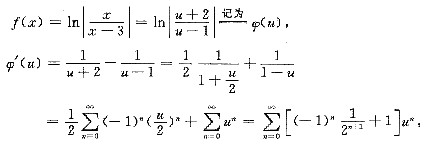
成立的范围是
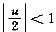
与|u|＜1中取小者，为|u|＜1．从而知
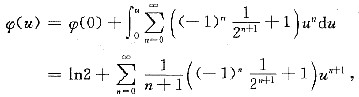
即有
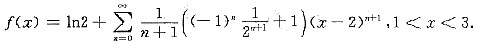
又因当x=3时上述级数发散，当x=1时上述级数收敛，且当x=1时f(x)连续，故知上述展开式成立的范围为1≤x＜3．
3. 设f(x,y)，ψ(x,y)均有连续偏导数，点M
0(x
0，y
0)是函数z=f(x,y)在条件ψ(x,y)=0下的极值点，又ψ'
γ(x
0，y
0)≠0，求证：
(Ⅰ)
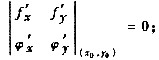
(Ⅱ)曲面z=f(x,y)与柱面ψ(x,y)=0的交线厂在点P
0(x
0,y
0,z
0)(z
0=f(x
0,y
0))处的切线与xy平面平行；
(Ⅲ)xy平面上的曲线f(x,y)=f(x
0，y
0)与曲线ψ(x,y)=0在点M
0处相切．
[分析与证明] (Ⅰ)由题设条件
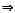
方程ψ(x，y)=0在点M0邻域确定隐函数y=y(x)，且满足y(x
0)=y
0．
M
0点是z=f(x，y)在条件ψ(x，y)=0下的极值点
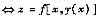
以x=x
0为极值点．它的必要条件是
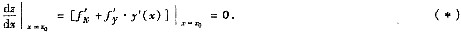
由ψ[x，y(x)]=0及隐函数求导法得
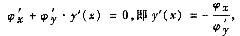
代入(*)得
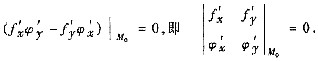
(Ⅱ)空间曲线
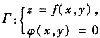
在P
0(x
0，y
0，z
0)处的切线的方向向量(切向量)为
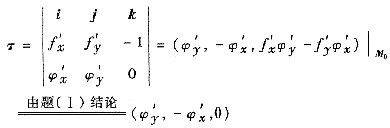
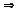
f与xy平面平行．
(Ⅲ)曲线f(x，y)=f(x
0，y
0)与曲线ψ(x，y)=0在公共点M
0处的法向量分别是gradf(x，y)|M
0=(f'
x，f'
y，)|M
0与gradψ(x，y)|M
0=(ψ'
x，ψ'
y)|M
0，由题(Ⅰ)知，gradf(x，y)M
0与gradψ(x,y)|M
0平行
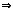
这两条曲线在点M
0处相切．
4.
5. 设f(x)是在[a,b]上的连续、严格单调函数，在(a,b)内可导，且f(a)=a＜b=f(b)，试证：在(a,b)内必存在n个不同的点η
i(i=1,2，…,n)，
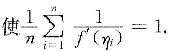
将[a,b]n等分，分点为a=x
0＜x
1＜x
2＜…＜x
n=b，
于是
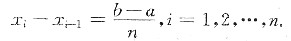
由于f(x)在[a,b]上连续，严格单调，f(a)=a，f(b)=b，故由连续函数介值定理，有
f(ξ
i)=x
i，i=1，2，…，n．
令ξ
0=a，ξ
n=b，由单调性，有
ξ0＜
ξ
1＜ξ
2＜…＜ξ
n，
在每一个[ξ
i-1，ξ
i]上应用拉格朗日中值定理，有
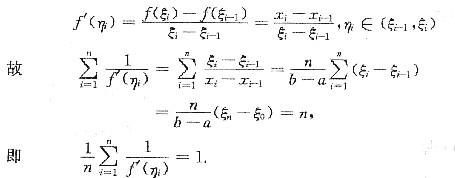
[分析] 利用连续函数性质及拉格朗日中值定理证之．
6.
7. 设X
1，X
2，…，X
n是来自总体X的简单随机样本，X的概率密度为
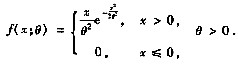
试求：(Ⅰ)θ的矩估计量，并判定其是否为θ的无偏估计量；
(Ⅱ)θ的最大似然估计量．
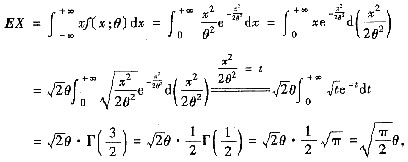
从而
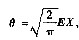
故θ的矩估计量
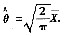
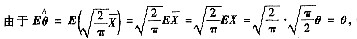
所以
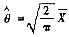
是θ的无偏估计量．
(Ⅱ)未知参数θ的似然函数和对数似然函数分别为
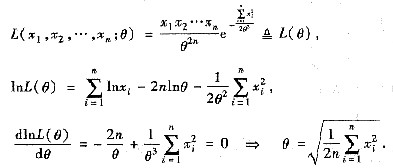
故θ的最大似然估计量
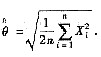
8.
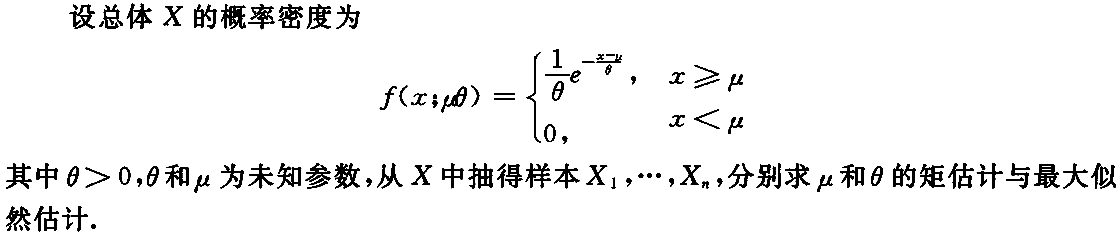
9. 确定常数a与b的值，使得
．
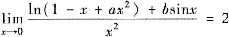
把ln(1-x+ax
2)与sinx的带皮亚诺余项的麦克劳林公式
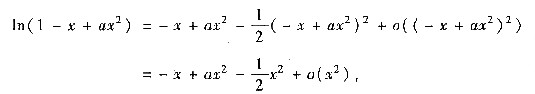
sinx=x+o(x
2)
代入题设的极限可得
是一个一阶线性方程．
若f(x)在x=1处可导，则α的取值为
而上述极限存在且为零的充分必要条件是α+1＜0，即α＜-1；又f'-(1)=0，故应选(A)．
深色：已答题 浅色：未答题