三、解答题1.
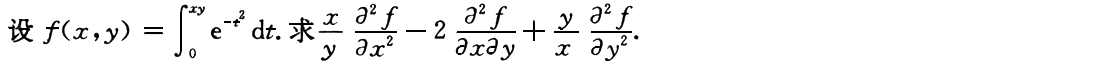
2. 设
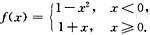
求
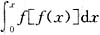
及
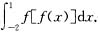
由复合函数概念知，当x＜-1时，f(x)=1-x
2＜0，故
f[f(x)]=1-[f(x)]
2=1-(1-x
2)
2=2x
2-x
4，
当-1≤x＜0时，f(x)=1-x2
≥0，故
f[f(x)]=1+f(x)=1+(1-x
2)=2-x
2，
当x≥0时，f(x)=1+x＞0，故
f[f(x)]=1+f(x)=1+(1+x)=2+x，
综上有
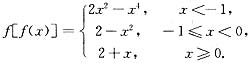
于是，当x＜-1时，
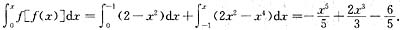
当-1≤x＜0时，
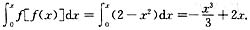
当x≥0时，
从而
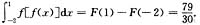
3. 已知对于n阶方阵A，存在自然数k．使得A
k=0，试证明：矩阵E-A为可逆矩阵并求它的表达式(E为n阶单位矩阵)。
由代数公式1-ak=(1-a)(1+a+…+ak-1)以及A与E可交换，有
E-Ak=(E-A)(E+A+…+Ak-1)．而Ak=0，
故有(E-A)(E+A+…+Ak-1)=E．
可知E-A可逆，且有
(E-A)-1=E+A+…+Ak-1
[评注] 抽象矩阵可逆性的证明或求逆常用定义法，即设法得到等式AB=E．此时，A，B可逆，且互为逆矩阵．
[考点提示] 单位矩阵、逆矩阵．
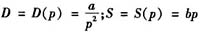(a＞0，b＞0为常数)
价格p是时间t的函数，且满足方程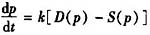
(k＞0为常数)，假定t=0时，价格为1，试求4. 需求量等于供给量时的均衡价格；
由
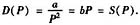
，得均衡价格
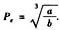
6.
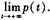
7. 求幂级数
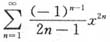
的收敛半径R，收敛域D以及和函数S(x)．
当x=0时幂级数
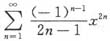
是收敛的，当x≠0时由于
可见当0＜|x|＜1时幂级数绝对收敛，当|x|＞1时幂级数发散，故幂级数的收敛半径R=1．
当x=±1时幂级数成为交错级数
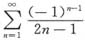
，由于数列
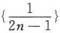
单调减少且趋于零，故幂级数当x=±1时也收敛，即幂级数的收敛域为闭区间[-1，1]．
令幂级数的和函数为S(x)，即
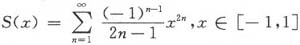
．由于
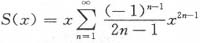
，记
．当|x|＜1时逐项求导得
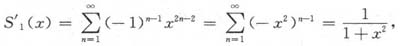
将上式逐项求积分，并利甩S
1(0)=0即得当|x|＜1时
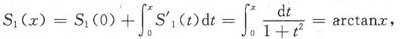
代入即得
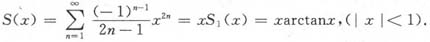
由于幂级数
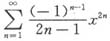
在x=±1收敛，从而S(x)在[-1，1]上连续．注意xarctanx在x=±1也连续，故S(x)=xarctanx不仅当|x|＜1时成立，而且在x=±1也成立．即有
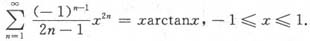
8. 设矩阵A满足A(E-C
-1B)
TC
T=E+A，其中
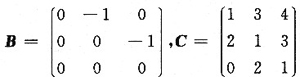
，求矩阵A．
由A(E-C-
1B)
T=E+A得
A[C(E-C
-1B)]
T=E+A，
即E+A=A(C-R)
T，E=A[(C-B)-E]
T，
而
证明：9. A
2=A的充分必要条件是ξ
Tξ=1．
由A
2=(E-ξξ
T)(E-ξξ
T)=E-2ξξ
T+ξξ
Tξξ
T =E-2ξξ
T+ξ(ξ
Tξ)ξ
T=E-ξξ
T+(ξ
Tξ-1)ξξ
T =A+(ξ
Tξ-1)ξξ
T 那么A
2=A
(ξ
Tξ-1)ξξ
T=0
因为ξ是非零列向量，ξξ
T≠0．
所以 A
2=A
ξ
Tξ=1．
10. 当ξ
Tξ=1时，A是不可逆矩阵．
当ξTξ=1时，由(Ⅰ)知A2=A．那么如果A可逆，则有
A=A-1A2=A-1A=E
与A=E-ξξT≠E相矛盾．
11.
12.
深色：已答题 浅色：未答题