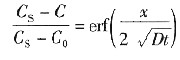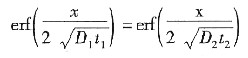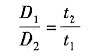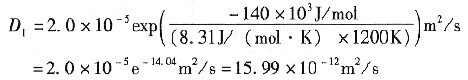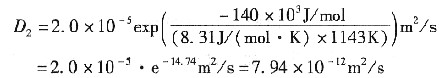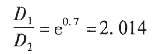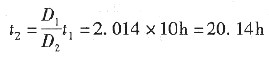二、填空如果晶体中不同的原子面用A、B、C、D等字母来表示,面心立方晶体中原子的堆垛方式为 1 ,密排六方晶体原子的堆垛方式为 2 。3. 原子或离子的
是指在晶体结构中,该原子或离子的周围与它直接相邻结合的原子个数或所有异号离子的个数。
8. 由一个固相同时析出成分和晶体结构均不相同的两个新固相的过程称为
转变。
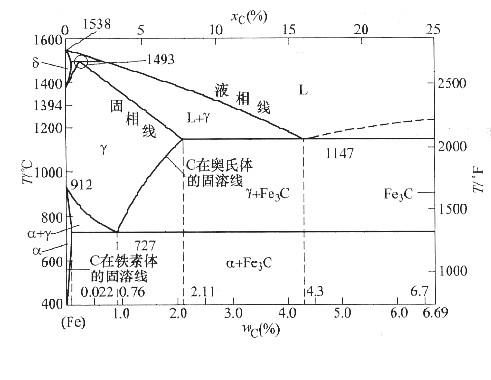
9. 在合金平衡相图中,确定一定温度和合金组分下合金内存在的各相的比例时,可以通过等温连接线,利用
定律进行计算。
10. 在均一的液相中靠自身的结构起伏和能量起伏等条件形成晶核的方式称为
形核。
14. 金属多晶体塑性变形至少需
独立滑移系开动。
四1. 用四指数表示的密排六方结构的原子最密排面和最密排方向是什么?试证明理想密排六方晶胞的晶格常数比(轴比)c/a为1.633。
用四指数表示的密排六方结构的原子最密排面为{0001},用四指数表示的密排六方结构的原子最密排方向为
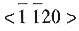
。
证明:密排六方晶胞的1/3如图8-2所示。
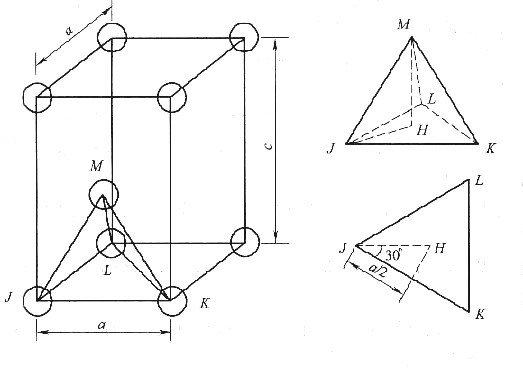
考虑由JKLM构成的四面体
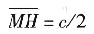
由于在J、K和M处的原子相互接触,因此
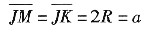
在JHM三角形中

在JKL等边三角形中解出
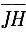
的长度
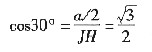
即
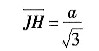
将JH代入,得
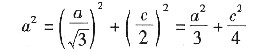
由此解出

五1. 以圆圈表示一个原子,试画出体心立方晶体中(111)面的原子排列方式,要求至少画出十个以上的原子。
如图8-3所示。

六1. 实验中发现,在α-Fe中可以通过
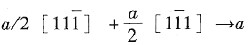
[100]反应形成[100]位错,在Fe的晶胞中表示这一反应,并证明此位错反应可以发生。
如图8-4所示。
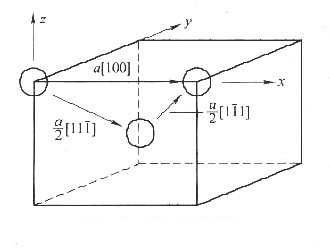
证明:
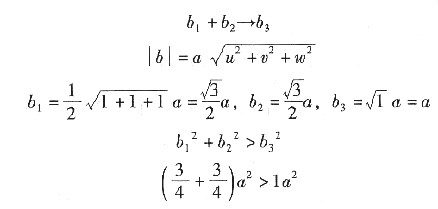
因此反应可以发生。
七1. 金属中空位平衡浓度随温度的变化规律遵循N
V=Nexp(-Q
V/RT)。某金属在被加热到1130K的时候,其空位的平衡浓度是其在1000K时的5倍。假设在1000~1130K之间金属的密度不变,气体常数为8.31J/(mol·K),试计算其空位形成能Q
V。
在1130K和1000K的空位平衡浓度分别为N
V1和N
V2,那么
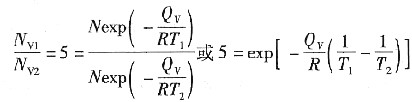
这样可以求解Q
V 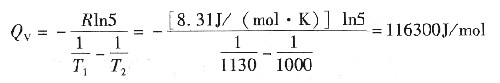
十1. 塑性变形金属的显微组织、晶内结构发生什么变化?性能发生哪些变化?
金属发生塑性变形后,显微组织形态上,原等轴晶粒沿变形方向被拉长,在大变形量时晶界甚至呈纤维状,如存在硬脆的第二相颗粒或夹杂,常沿变形方向呈带状分布。
显微结构上,缺陷(空位和位错)密度明显增大。由于变形过程中位错的增殖及运动过程中位错的交割和交互作用,形成位错缠结,异号位错相消后构成胞状结构。随变形量增加,位错胞数量增多,尺寸减小,晶体内部的储存能增大。性能上,冷变形金属将发生加工硬化,表现为强度显著提高、塑性明显下降。
十一1. 马氏体的强化要素有哪些?请详细说明马氏体的强度和韧性与其含碳量、组织形态及亚结构的关系。
马氏体的强化要素有碳原子的间隙固溶强化作用;C原子团簇对位错的钉扎作用;C原子进入马氏体晶体结构的扁八面体中心,造成非对称点阵膨胀(形成畸变偶极应力场),产生的强烈的间隙固溶强化作用;晶界、位错、孪晶的强化作用。
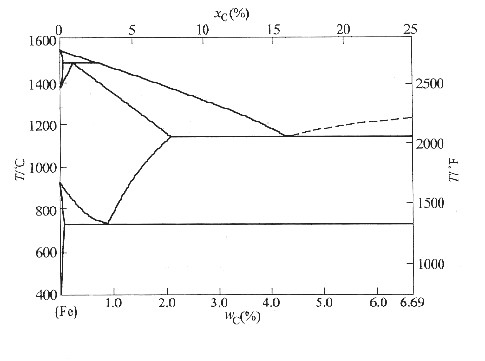
马氏体的强度和韧性与其含碳量、组织形态及亚结构密切相关。铁碳合金中,含碳量wC<0.3%,形成板条状马氏体,具有位错亚结构,强度较低,塑性和韧性好;wC>1.0%,形成片状马氏体,具有孪晶亚结构,强度高,但塑性和韧性差;0.3%<wC<1.0%形成板条马氏体+片状马氏体的混合组织,具有位错和孪晶的混合亚结构,可获得优良的强韧性综合性能。
十二1. 影响晶态固体中原子扩散的因素有哪些?并加以简单说明。
(1) 温度:温度越高,扩散系数越大,扩散速率越快。
(2) 晶体结构及固溶体类型:致密度较小的晶体结构中扩散激活能较小,扩散易于进行;对称性较低的晶体结构,扩散系数的各向异性显著;间隙固溶体中的扩散激活能远小于置换固溶体,扩散容易进行。
(3) 第三组元:根据加入的第三组元的性质不同,有的促进扩散,有的阻碍扩散;
(4) 晶体缺陷:沿晶界的扩散系数远大于体扩散系数;沿位错管道扩散时扩散激活能较小,因而位错加速扩散。
十三1. 已知碳在γ-Fe中的扩散常数D
0=2.0×10
-5m
2/s,扩散激活能Q=140×10
3J/mol,要想得到与在927℃时渗碳10h的相同厚度,在870℃渗碳需要多长时问?(忽略不同温度下碳在γ-Fe中溶解度的不同)
碳在γ-Fe中扩散的误差函数解表示为
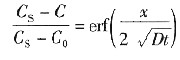
碳在927℃与870℃两种条件下分别扩散的误差函数间关系为
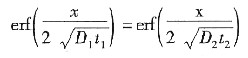
即
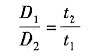
碳在γ-Fe中的扩散系数为D=D
0exp(-Q/RT)
碳在927℃条件下的扩散系数为
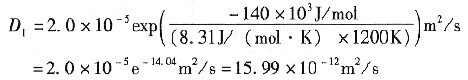
碳在870℃条件下的扩散系数为
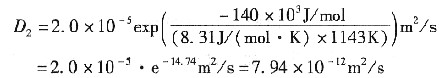
计算可得
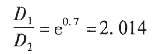
则所需时间为
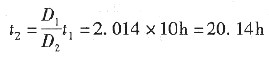
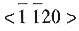 。
。 
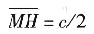
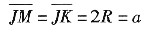

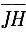 的长度
的长度 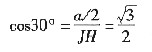
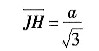
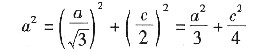


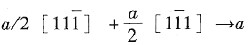 [100]反应形成[100]位错,在Fe的晶胞中表示这一反应,并证明此位错反应可以发生。
[100]反应形成[100]位错,在Fe的晶胞中表示这一反应,并证明此位错反应可以发生。 
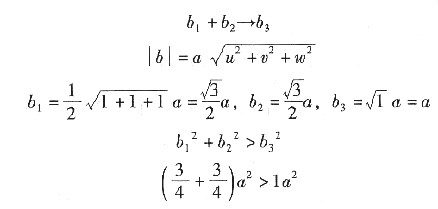
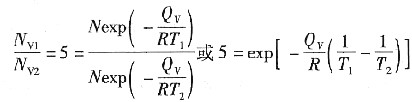
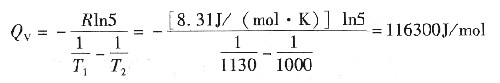
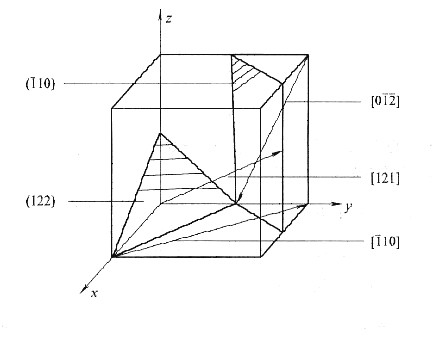
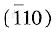 晶面,及[121]、
晶面,及[121]、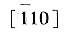 、
、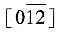 晶向。
晶向。