二、是非判断并改错1. 在密排六方晶体中,(110)、
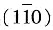
、
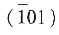
、(101)、(011)和
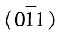
都是属于同一个晶面族。
错。在密排六方晶体中若用三指数表示法,则(110)、
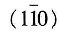
、
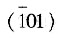
、(101)、(011)和
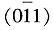
所表示的分别是其柱面和锥面,它们不属于同一个晶面族。
2. 中间相只是包括那些位于相图中间且可以用一个分子式表示的化合物相。
错。凡是位于相图中间的各种合金相结构都统称为中间相,这其中当然包括一个分子式表示的化合物相以及一些固溶体相。
3. 低碳钢渗碳处理时,一般都在950℃的高温下进行,这是因为此时碳原子的活动能力强,有利于扩散的快速进行。
错。主要原因是在950℃的高温下低碳钢的组织为奥氏体,碳在奥氏体的溶解度可以达到最大值。
4. 多条刃型位错线堆积在一起就形成了一条滑移线。
错。只有当约1000条位错线移出晶体表面,才会在晶体表面形成一条滑移线。
5. 采用适当的再结晶退火,可以细化金属铸件的晶粒大小。
错。只有经过一定量塑性变形的金属材料,采用适当的再结晶退火,才可以达到细化晶粒大小的目的。金属铸件一般不能经受一定量的塑性变形,所以不能细化其晶粒大小。
三、完成下列各题设在简单立方晶体中有一个位于滑移面ABCD上的位错环abcd,其柏氏矢量b、所受切应力τ如图19-1所示,回答下列问题:
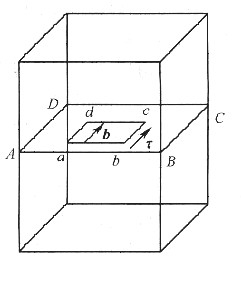
1. 指出位错环abcd中各段位错线的类型。
位错线节和位错线cd的方向矢量都和其柏氏矢量b垂直,故它们属于刃型位错;而位错线bc和位错线da的方向矢量都和其柏氏矢量b平行,故它们属于螺型位错。
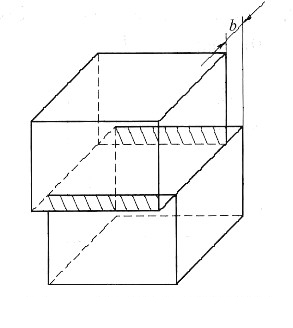
2. 画出位错环abcd移出晶体后晶体所产生的滑移量及所产生变形的方向。
位错环abcd全部移出晶体后,晶体会产生宽度为一个柏氏矢量的滑移量,所产生变形的方向与切应力τ的方向一致,如图19-2所示。
3. 有一铝单晶体的试样表面为(100),如该晶体的各个滑移系都可以进行滑移,则在试样表面可能看到的滑移线形貌(即滑移线的取向和它们之间的夹角)是什么?
铝是面心立方晶体,它的滑移系是{111}<110>,共有12个具体的滑移系。现在,铝单晶体试样表面为(100)。当发生塑性变形时,晶体表面所产生的滑移线应该是既位于各个{111}面上,又位于(100)面上,即位于(111)、
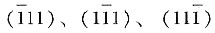
四个滑移面与(100)面的交线上,应该是
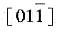
和[011],而这两个方向又互相垂直,同向的滑移线又互相平行。因此,可以看到的这些滑移线在(100)面呈现互相平行或者互相垂直的组态。
五、完成下列各题1. 画出Fe-Fe
3C的平衡相图,并填写相区。
所画出Fe-Fe
3C的平衡相图,如图19-4所示。各个相区的填写,如图19-4中所注。
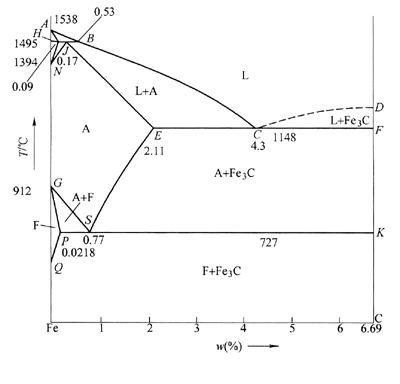
2. 具体说明相图中有几个单相区、几个两相区和几个三相平衡反应。
Fe-Fe3C的平衡相图中有5个单相区,即液相区、高温铁素体区、铁素体区F、奥氏体区A和渗碳体区。
Fe-Fe3C的平衡相图中有7个两相区,即(L+δ)、(L+A)、(A+δ)、(A+F)、(L+Fe3C)、(F+Fe3C)、(A+Fe3C)。
Fe-Fe3C的平衡相图中有3个三相平衡反应。
3. 说明相图中各水平线的相变过程、相变产物及反应条件。
包晶转变L+δ→A,反应产物是奥氏体。发生在1495℃,三相的成分wC分别为0.53%、0.09%和0.17%
共晶转变L→A+Fe3C,反应产物是莱氏体。发生在1148℃,三相的成分wC分别为4.30%、2.11%和6.69%
共析转变A→F+Fe3C,反应产物是珠光体。发生在727℃,三相的成分wC分别为0.77%、0.0218%和6.69%
4. 说明w
C=0.40%的铁-碳合金从液态平衡冷却到室温时的相变过程和最终平衡组织,并计算其中各个相的相对含量。
在1495℃以上,液相中析出高温铁素体δ。
在1495℃时,发生包晶转变L+δ→A,反应产物是奥氏体。
在1495~800℃之间,奥氏体冷却。
在800~727℃之间,奥氏体中析出铁素体F。
在727℃时,发生共析转变A→F+Fe
3C,反应产物是珠光体。
在727℃以下,从铁素体F中析出三次渗碳体。
室温时,w
C=0.40%的铁一碳合金的最终平衡组织是先共析铁素体+珠光体+三次渗碳体,平衡相为铁素体+渗碳体,其相对含量分别为
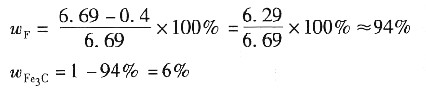
六、完成下列各题1. 有一个铝单晶体试样,在拉伸前的滑移方向与拉伸轴的夹角为45°,拉伸后的滑移方向与拉伸轴的夹角为30°,试求铝单晶体试样拉伸后所产生的延伸率为多少。
铝单晶体试样拉伸前、后的示意图如图19-5所示。图中AC和A'C'分别表示试样拉伸前、后晶体中两个相邻滑移面之间的距离,即滑移面的面间距。
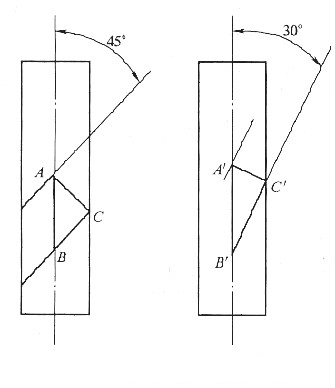
显然,试样拉伸前、后晶体中两个相邻滑移面之问的面间距是不会改变的,即AC和A'C'相等。于是,铝单晶体试样拉伸后所产生的延伸率应为:
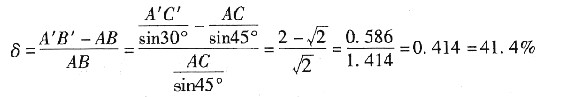
2. 三元合金相图中的垂直截面与二元合金相图有何不同?为什么二元合金相图可以使用杠杆定律来分析各个相的相对含量,而三元合金相图中的垂直截面却不能?
三元合金相图中垂直截面的两端并不是纯组元,而是一端纯组元、另一端二元合金,甚至两端都是二元合金。另外,在二元合金相图中纯组元的相变点只有一个,而在三元合金相图的垂直截面中,其两端往往是开口的,即有两个相变点。因此,它与二元合金相图不同,是一个伪二元合金相图。
杠杆定律表示在一定的温度下,合金两个相的相对含量与合金成分点到两个相区线的距离成反比。杠杆定律的应用必须保证自由度为零的条件。在三元合金相图中的垂直截面中,即使温度一定,此时的自由度f=c-p=3-2=1,也不满足自由度为零的条件。因此,在三元合金相图中的垂直截面中,不能使用杠杆定律来分析各个相的相对含量。