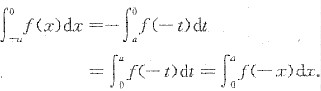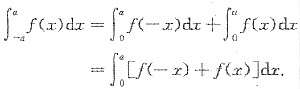一、选择题8. 设区域D={(x,y)|x
2+y
2≤1,x≥0,y≥0),则在极坐标系下,二重积分
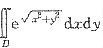
可表示为
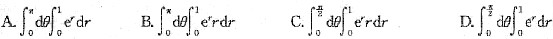
A B C D
C
[解析] 因为区域D:x
2+y
2≤1,x≥0,y≥0,令
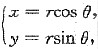
有0≤r≤1,0≤θ≤
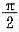
,故选C.
9. 下列级数中,条件收敛的级数是

A B C D
C
[解析] 对于A中所给级数
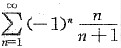
,由于
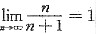
,可知
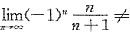
0,因此
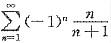
发散,应排除A对于B中所给级数
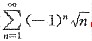
,由于
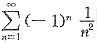
,可知

,因此
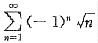
发散.对于D中所给级数
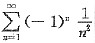
,考虑
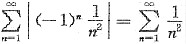
为p=2的p级数,可知其为收敛级数,从而知
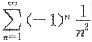
为绝对收敛,应排除D.对于C中所给级数
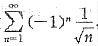
,由于
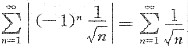
为

的p级数,可知其发散.但是,注意到
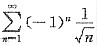
为交错级数,且
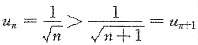
,
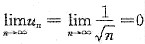
,由莱布尼茨定理可知
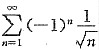
收敛,从而知其为条件收敛.故选C.
二、填空题把答案填在题中横线上.
1. 设f(x)在x=1处连续,且
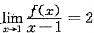
,则f'(1)=______.
2
[解析] 由题设条件,有
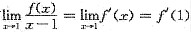
,则f'(1)=2.
2. 设
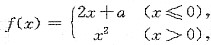
且f(x)在点x=0处连续,则a=______.
0
[解析] 本题考查的知识点为函数连续性的判定.
由于点x=0为函数的分段点,且在点x=0两侧f(x)的表达式不同,因此应考查左连续、右连续.
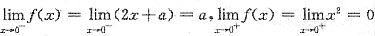
.
由于f(x)在点x=0连续,因此
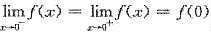
,从而a=0.
3.
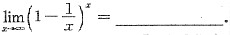
e-1
[解析]
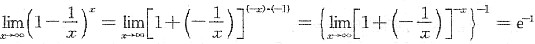
.
4. 函数y=x
2-2x在区间[1,2]上满足拉格朗日中值定理条件的ξ=______.
[解析] 因为y=x
2-2x在[1,2]上满足拉格朗日中值定理条件,则设f(x)=x
2-2x,有
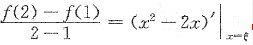
,即

,2ξ=3,所以
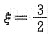
.
5. 若
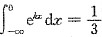
,则k=______.
3
[解析] 因为
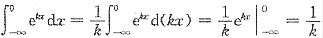
,所以
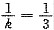
,k=3.
6. 已知f(x)的一个原函数为
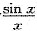
,则

.
7. 曲线
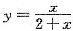
的铅直渐近线为______.
x=-2
[解析] 由于题目只求铅直渐近线,所给函数表达式为分式,可知
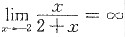
,因此所给曲线的铅直渐近线为x=-2.
8. 空间直角坐标系中方程y=x
2表示的曲线是______.
母线平行于z轴的抛物柱面
[解析] 本题考查二次曲面方程的识别.
9. 函数f(x,y)=4(x-y)-x
2-y
2的极大值点是______.
(2,-2)
[解析] 令
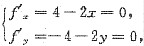
解得驻点为(2,-2).
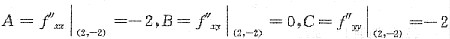
,则B
2-AC=-4<0有极值且A=-2<0,有极大值,所以极大值点为(2,一2).
10. 若级数
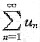
收敛于s,则
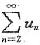
收敛于______.
三、解答题解答应写出推理、演算步骤.
1. 求证:当x>0时,e
x>1+x.
证明 作辅助函数f(t)=et,则f(t)在区间[0,x]上满足拉格朗日中值定理的条件,于是f(x)-f(0)=f'(ξ)(x-0)(0<ξ≤x),即 ex-1=eξx (0<ξ<x),又当0<ξ<x时,1<eξ<ex,故有ex-1=eξx>1·x=x,即ex>1+x(x>0).
[解析] 本题可用单调性的思想去证,即令f(x)=ex-1-x,f'(x)=ex-1>0(当x>0时),说明f(x)是增函数,即当x>0时,f(x)>f(0)=0,所以f(x)>0,则有ex>1+x.当然也可用下面方法证明.
2. 求极限
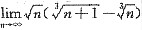
.
[解析] 此极限是“∞·(∞-∞)”,为不定型.而已知(a-b)(a
2+ab+b
2)=a
2-b
2,所以分子,分母同乘
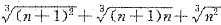
后分式变为
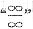
型.又根据当n→∞时,分母的次数高于分子的次序,所以所求极限为零.
3. 设
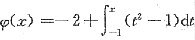
,试求ψ(x)的极值.
由ψ'(x)=x
2-1=0,得x=-1或x=1.
又ψ"(x)=2x,且ψ"(-1)=-2<0,ψ"(1)=2>0,故当x=-1时,ψ(x)取极大值
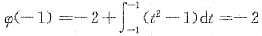
;
当x=1时,ψ(x)取极小值
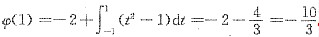
.
[解析] 这是一道求函数极值的题.只要用常规的求极值的方法去求就可以了.不过在求函数的导数时要注意变上限积分的导数公式的应用,即
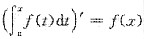
.
4. 设y=y(x)满足
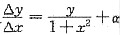
,当△x→0时,a为无穷小,求y.
由于当△x→0时,a为无穷小,可知
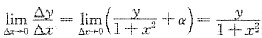
,从而有
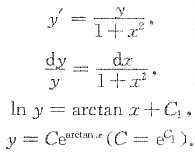
[解析] 在做本题时要注意导数的定义,即
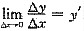
和一阶微分方程中变量可分离类的解法.
5. 已知平面π
1:kx-2y+3z-2=0与平面π
2:3x-2y-z+5=0垂直,试求参数k的值.
平面π
1,π
2的法向量分别为n
1={k,-2,3},n
2={3,-2,-1},由题设知,n
1与n
2垂直,于是有 n
1·n
2=0,即 3k+(-2)·(-2)+3·(-1)=0,解得:

.
[解析] 如果给出两个一般的平面方程π1:A1x+B1y+C1z+D1=0,π2:A2x+B2y+C2z+D2=0.则它们的法向量分别为n1={A1,B1,C1},n2={A2,B2,C2).如果这两个平面π1与π2垂直,则应满足n1·n2=0.即A1A2+B1B2+C1C2=0,具体解法如下:
6. 要造一个容积为32π立方厘米的圆柱形容器.其侧面与上底面用一种材料,下底面用另一种材料.已知下底面材料每平方厘米的价格为3元,侧面材料每平方厘米的价格为1元.问该容积的底面半径r与高h各为多少时,造这个容器所用的材料费用最少?
设S为材料费用函数,则S=2πrh+πr
2+3πr
2,且满足条件πr
2h=32π,所以
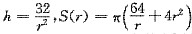
.
因
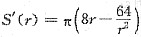
,令S'(r)=0,得驻点 r=2.
因S"(2)=24π>0,且驻点唯一,所以r=2为S(r)的最小值点,此时
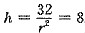
.
所以r=2厘米,h=8厘米时,材料费用最省.
[解析] 本题为利用导数求最值问题.
求最大值与最小值的一般方法是:
(1)求出f(x)在(a,b)内的所有(可能的极值点)驻点、导数不存在的点:x1,…,xk.
(2)求出上述各点及区间两个端点x=a,x=b处的函数值:f(x1),…,f(xk),f(a),f(b)进行比较,其中最大的数即为y=f(x)在[a,b]上的最大值,相应的x的取值即为f(x)在[a,b]上的最大值点,而其中最小的数值即为f(x)在[a,b]上的最小值,相应的x的取值即为f(x)在[a,b]上的最小值点.
7. 设平面薄片的方程可以表示为x
2+y
2≤R
2,x≥0,薄片上点(x,y)处的密度
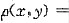
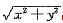
,求该薄片的质量M.
解法一 利用对称性.依题设
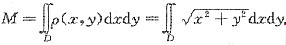
.
由于区域D关于x轴对称,
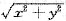
为x的偶函数,记D在x轴上方的部分为D
1,则
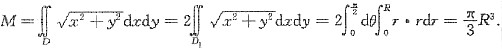
.
解法二
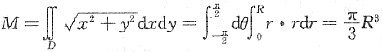
.
[解析] 由二重积分的物理意义知:该薄片的质量
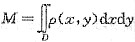
(其中ρ(x,y)为密度函数).而此积分的区域D为半圆即x
2+y
2≤R
2(x≥0).所以由下面解法可以得到质量M的结果.
8. 设函数f(x)在[-a,a](a>0)上连续,证明
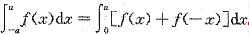
.
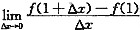

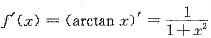 ;再由导数定义知:
;再由导数定义知: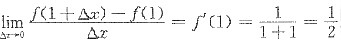 .故选C.
.故选C.
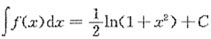 ,则
,则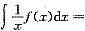
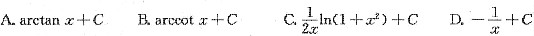
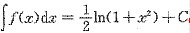 ,则
,则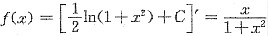 .
.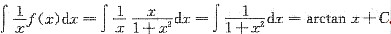 .故选A.
.故选A.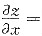
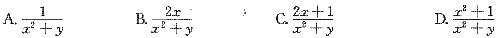
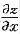 时,将y认定为常量,则
时,将y认定为常量,则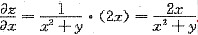 .故选B.
.故选B.
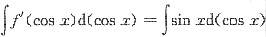 ,有
,有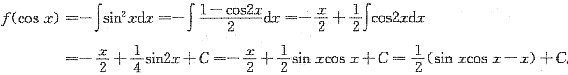 .
.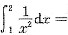

 .故选C.
.故选C.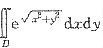 可表示为
可表示为 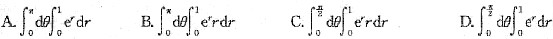
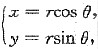 有0≤r≤1,0≤θ≤
有0≤r≤1,0≤θ≤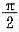 ,故选C.
,故选C.
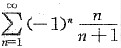 ,由于
,由于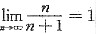 ,可知
,可知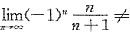 0,因此
0,因此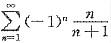 发散,应排除A对于B中所给级数
发散,应排除A对于B中所给级数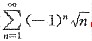 ,由于
,由于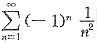 ,可知
,可知 ,因此
,因此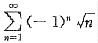 发散.对于D中所给级数
发散.对于D中所给级数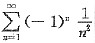 ,考虑
,考虑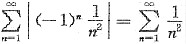 为p=2的p级数,可知其为收敛级数,从而知
为p=2的p级数,可知其为收敛级数,从而知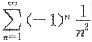 为绝对收敛,应排除D.对于C中所给级数
为绝对收敛,应排除D.对于C中所给级数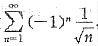 ,由于
,由于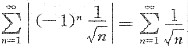 为
为 的p级数,可知其发散.但是,注意到
的p级数,可知其发散.但是,注意到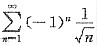 为交错级数,且
为交错级数,且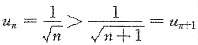 ,
,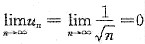 ,由莱布尼茨定理可知
,由莱布尼茨定理可知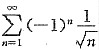 收敛,从而知其为条件收敛.故选C.
收敛,从而知其为条件收敛.故选C.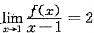 ,则f'(1)=______.
,则f'(1)=______.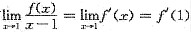 ,则f'(1)=2.
,则f'(1)=2.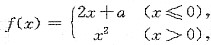 且f(x)在点x=0处连续,则a=______.
且f(x)在点x=0处连续,则a=______.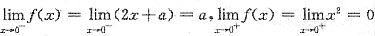 .
.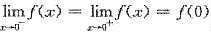 ,从而a=0.
,从而a=0.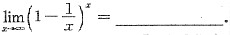
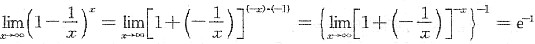 .
.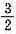
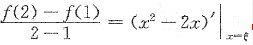 ,即
,即 ,2ξ=3,所以
,2ξ=3,所以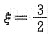 .
.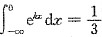 ,则k=______.
,则k=______.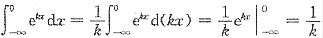 ,所以
,所以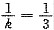 ,k=3.
,k=3.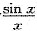 ,则
,则 .
.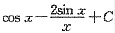
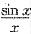 ,所以
,所以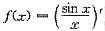 ,所以
,所以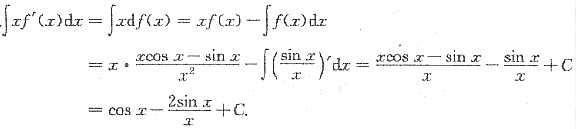
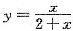 的铅直渐近线为______.
的铅直渐近线为______.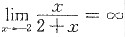 ,因此所给曲线的铅直渐近线为x=-2.
,因此所给曲线的铅直渐近线为x=-2.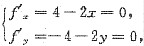 解得驻点为(2,-2).
解得驻点为(2,-2).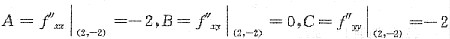 ,则B2-AC=-4<0有极值且A=-2<0,有极大值,所以极大值点为(2,一2).
,则B2-AC=-4<0有极值且A=-2<0,有极大值,所以极大值点为(2,一2).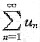 收敛于s,则
收敛于s,则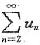 收敛于______.
收敛于______.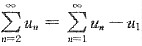 ,而
,而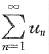 收敛于s.则
收敛于s.则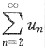 收敛于s-u1.
收敛于s-u1.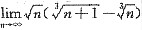 .
.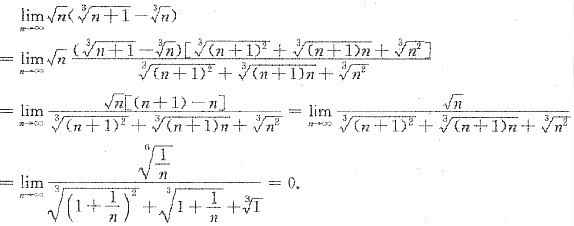
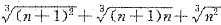 后分式变为
后分式变为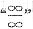 型.又根据当n→∞时,分母的次数高于分子的次序,所以所求极限为零.
型.又根据当n→∞时,分母的次数高于分子的次序,所以所求极限为零.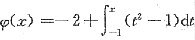 ,试求ψ(x)的极值.
,试求ψ(x)的极值.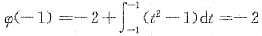 ;
;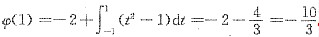 .
.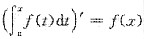 .
.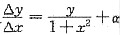 ,当△x→0时,a为无穷小,求y.
,当△x→0时,a为无穷小,求y.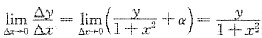 ,从而有
,从而有 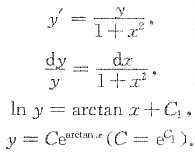
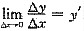 和一阶微分方程中变量可分离类的解法.
和一阶微分方程中变量可分离类的解法. .
.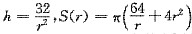 .
.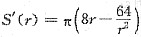 ,令S'(r)=0,得驻点 r=2.
,令S'(r)=0,得驻点 r=2.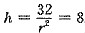 .
.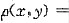
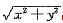 ,求该薄片的质量M.
,求该薄片的质量M.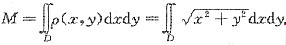 .
.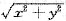 为x的偶函数,记D在x轴上方的部分为D1,则
为x的偶函数,记D在x轴上方的部分为D1,则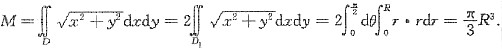 .
.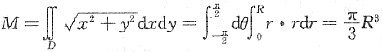 .
.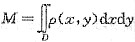 (其中ρ(x,y)为密度函数).而此积分的区域D为半圆即x2+y2≤R2(x≥0).所以由下面解法可以得到质量M的结果.
(其中ρ(x,y)为密度函数).而此积分的区域D为半圆即x2+y2≤R2(x≥0).所以由下面解法可以得到质量M的结果.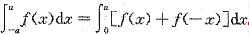 .
.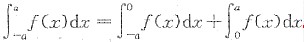 .
.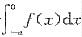 ,令x=-t,则
,令x=-t,则