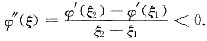一、选择题下列每小题给出的四个选项中,只有一项符合题目要求.1. “对任意给定的ε∈(0,1),总存在正整数N,当n≥N时,恒有|x
n-a|≤2ε”是数列{x
n}收敛于a的______.
- A.充分条件但非必要条件
- B.必要条件但非充分条件
- C.充分必要条件
- D.既非充分条件又非必要条件
A B C D
C
[解析] 数列极限的定义.
[解题分析] 本题考查数列极限的ε-N语言定义,
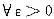
即>0,存在N∈N,当n>N时.有|x
n-a|<ε.将此定义与题设所给条件相比较,知两者实质是相同的,因此题设条件也是{x
n}收敛于a的充要条件,所以选C.
2. 设函数y=y(x)由参数方程
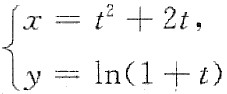
确定,曲线y=y(x)在x=3处的法线与X轴交点的横坐标是______.
A.
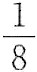
ln2+3 B.
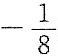
ln2+3
C.-8ln2+3 D.8ln2+3
A B C D
A
[解析] 法线方程、切线斜率.
[解题分析] 由题意可知,当x=3时,t=1和t=-3(不合题意,舍去),有
y=ln2,
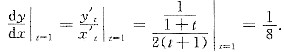
求得y=y(x)在x=3处的法线方程为
y=ln2-8(x-3).
令y=0,得法线与x轴交点的横坐标为x=
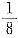
ln2+3.所以选A.
3. 设f(x)连续,F(x)=

f(t
2)dt,则F'(x)等于______.
- A.f(x4)
- B.x2f(x4)
- C.2xf(x4)
- D.2xf(x2)
A B C D
C
[解析] 按照变限积分求导法求导即可.
[解题分析] F'(x)=
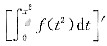
=f[(x
2)
2]·(x
2)'=2xf(x
4).
故应选C.
[评注] 一般地,对于变限积分
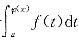
,其求导公式为
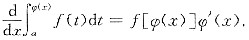
4. 设函数y=f(x)在(0,+∞)内有界且可导,则______.
A.当
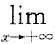
f(x)=0时,必有
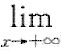
f(x)=0
B.当
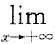
f'(x)存在时,必有
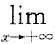
f'(x)=0
C.当
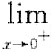
f(x)=0时,必有
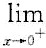
f'(x)=0
D.当
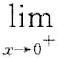
f'(x)存在时,必有
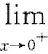
f'(x)=0
A B C D
B
[解析] 函数极限、导数的极限.
[解题分析] 由题设,可采取举反例的方法逐一排除干扰项.
关于A,设
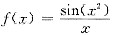
,则
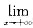
f(x)=
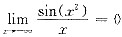
.但
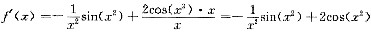
,其中2cos(x
2)项当x→∞时极限不存在,即
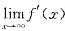
不存在.所以A可排除.
关于C和D,令f(x)=sinx,则
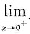
f(x)=0,且
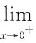
f'(x)=
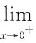
cosx=1.
从而C和D都可排除.
关于B的正确性,证明如下:
任取x>0,由拉格朗日中值定理,
f(2x)-f(x)=f'(ξ)·x (其中x<ξ<2x), ①
当x→+∞时ξ→+∞,由题设
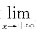
f'(x)存在,记为
A=
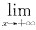
f'(X)=f'(+∞).
A为有限常数,在①中令x→+∞,则:
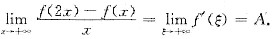
已知f(x)连续有界,因此
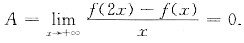
所以
f'(x)=0,综上,选B.
5. 设常数k>0,函数f(x)=
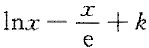
在(0,+∞)内零点的个数为______.
A B C D
B
[解析] 利用中值定理讨论零点的存在性,利用单调性确定零点的个数.
[解题分析] 因为f'(x)
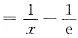
,令f'(x)=0,得x=e.
易知f(x)在(0,e)内单调增加,在(e,+∞)内单调减少,且f(e)=k>0.而
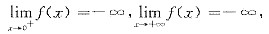
可见在f(x)在(0,e)和(e,+∞)分别有且只有一个零点,从而f(x)在(0,+∞)内有两个零点.
[评注] 只由f(e)=k>0,f(x)在(0,e)和(e,+∞)内的单调性,不能得零点的存在性.
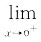
f(x)=-∞,
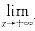
f(x)=-∞是确定零点存在性的重要条件.
6. 曲线
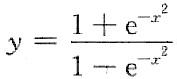
______.
- A.没有渐近线
- B.仅有水平渐近线
- C.仅有铅直渐近线.
- D.既有水平渐近线又有铅直渐近线
A B C D
D
[解析] 曲线的渐近线.
[解题分析] 因为
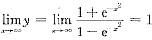
,所以y=1为其水平渐近线.
又
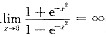
,所以x=0为其铅直渐近线.
可见曲线
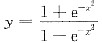
既有水平渐近线又有铅直渐近线,故应选D.
[评注] 若
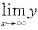
不存在,则应继续考虑
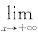
y或
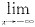
y,其中任何一个存在均说明有水平渐近线(y轴正向或负向);同样对于不连续点x
0,若
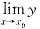
不存在且非无穷大量,则应继续考虑
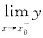
或
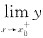
,其中任何一个为无穷大量.均说明x=x
0为铅直渐近线.
8. 设函数f(x)在(-∞,+∞)内有定义,x
0≠0是函数f(x)的极大值点,则______.
A.x
0必是f(x)的驻点 B.-x
0必是-f(-x)的极小值点
C.-x
0必是-f(x)的极小值点.D.对一切x都有f(x)≤f(x
0)
A B C D
B
[解析] 利用极大值的定义选择正确答案.
[解题分析] 用排除法:由于不可导点也可取极值,所以A不正确.注意到极值的局部性,知D也不正确.对于f(x)=-|x-1|,在x0=1处取极大值,但-x0=-1,并非是-f(x)=|x-1|的极小值点,所以C也不成立.故应选B.
二、填空题1.
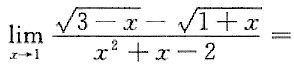
______.
[解析] 极限.
[解题分析]
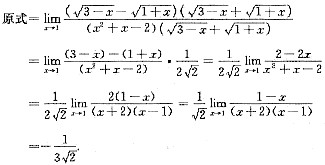
2.
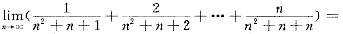
______.
[解析] 将数列的通项适当放大、缩小,再用夹逼准则即可.
[解题分析] 因为
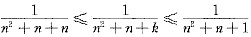
,
于是
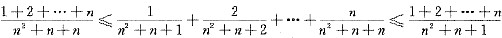
.
而
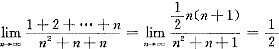
,
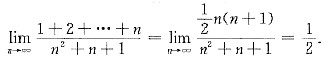
故根据夹逼准则知,
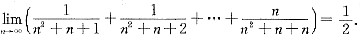
3. 设函数y=f(x)由方程xy十2lnx=y
4所确定,则曲线y=f(x)在点(1,1)处的切线方程是______.
y=x
[解析] 隐函数求导、切线方程.
[解题分析] 由题设所给方程xy+2lnx=y
4,两边对x求导,得
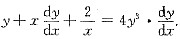
将x=1,y=1代入上式,得
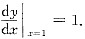
所以点(1,1)处的切线方程是y-1=x-1,即y=x.
4. 曲线
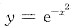
的上凸区间是______.
[解析] 求二阶导数,并由其符号确定曲线的上凸区间.
[解题分析] 对
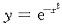
求一阶、二阶导数,得
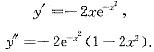
当y"<0,即x∈
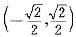
时,曲线向上凸.
5. 微分方程xy'+2y=xlnx满足y(1)=-
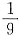
的解为______.
[解析] 一阶线性方程.
[解题分析] 将原方程变形为
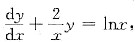
即
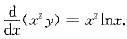
积分得
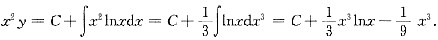
因为y(1)=-
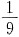
,得C=0,所以
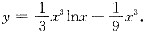
6. 设函数z=z(x,y)由方程z=e
2x-3z+2y确定,则
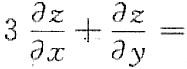
______.
2
[解析] 二元函数的偏导数.
[解题分析] 在方程z=e
2x-3x+2y两边分别对x,y求偏导,得
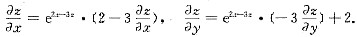
于是
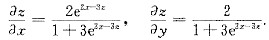
所以
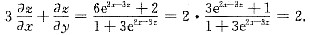
三、解答题1. 求极限
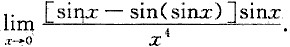
.
2. 求微分方程xy'+1=xe
x满足y(1)=1的特解.
先化为一阶线性微分方程的标准形式
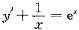
.由一阶线性微分方程的通
解公式,得
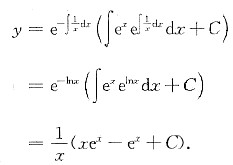
代入初始条件y(1)=1,得C=1,
所以所求特解为

[解析] 微分方程的特解.
3. 已知曲线的极坐标方程是r=1-cosθ,求该曲线上对应于
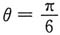
处的切线与法线的直角坐标方程.
[解题分析]由题设,曲线极坐标方程为r=1-cosθ,则曲线的直角坐标参数方程为
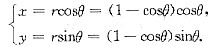
当
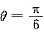
时,
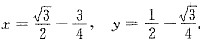
该点切线斜率为
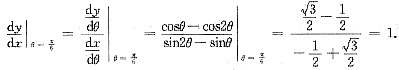
因此,该点切线方程为
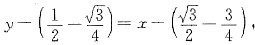
化简得
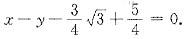
该点法线方程为
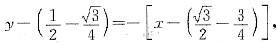
化简得
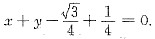
[解析] 切线方程、法线方程.
4. 设f(lnx)=
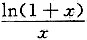
,计算∫f(x)dx.
由已知条件,应先求出f(x)的表达式,再进行积分.由于f(lnx)
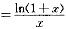
,因此令t=lnx,即x=e',代入上式得

则
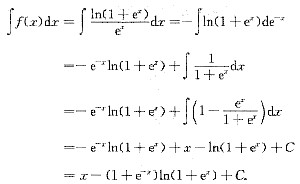
[解析] 不定积分.
5. 求微分方程y"+4y'+4y=e
ax的通解,其中a为实数.
方程y"+4y'+4y=e
ax对应的齐次方程的特征方程为:λ
2+4λ+4=0,特征根为λ
1=λ
2=-2,故对应的齐次方程通解为(C
1+C
2x)e
-2x.
当a≠-2时,即a不是特征根,方程的特解可设为y
*=Ae
ax,代入原方程得
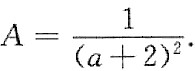
于是方程的通解为
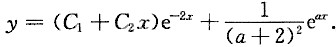
当a=-2时,即a为特征方程的二重根,方程的特解可设为
y
*=Ax
2e
-2x,代入原方程得
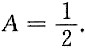
于是方程的通解为
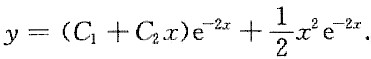
综上所述,方程的通解为
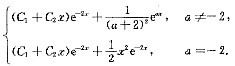
[解析] 对于二阶常系数非齐次线性微分方程,先求出对应齐次方程的特征方程的特征根及方程的通解,再根据特征根及自由项确定非齐次方程的特解的形式,代入方程求出特解.非齐次线性方程的通解为对应齐次方程的通解加上非齐次方程的特解.本题关键在于要注意特解y*的形式与a的取值有关.
6. 确定常数a,使向量组α
1=(1,1,a)
T,α
2=(1,a,1)
T,α
3=(a,1,1)
T可由向量组β
1=(1,1,a)
T,β
2=(-2,a,4)
T,β
3=(-2,a,a)
T线性表示,但是向量组β
1,β
2,β
3不能由向量组α
1,α
2,α
3线性表示.
根据题意得α
1,α
2,α
3可由向量组β
1,β
2,β
3线性表示,所以3个方程组x
1β
1+x
2β
2+x
3β
3=α(i=1,2,3)均有解.对增广矩阵作初等行变换,有
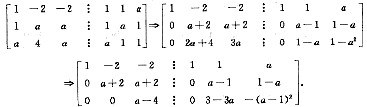
可见a≠4且a≠-2时,α
1,α
2,α
3可由β
1,β
2,β
3线性表示.
向量组β
1,β
2,β
3不能由向量α
1,α
2,α
3线性表示,即有3个方程组
x
1α
1+x
2α
2+x
3α
3=β
j(j=1,2,3)
均无解.对增广矩阵作初等变换,有
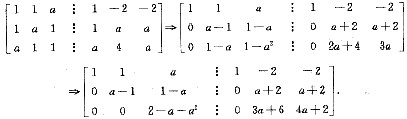
所以a=1时向量组α
1,α
2,α
3可由向量组β
1,β
2,β
3线性表示,但β
1,β
2,β
3不能由α
1,α
2,α
3线性表示.
[解析] 线性方程组求解、向量组线性表示.
7. 设n元线性方程组Ax=b,其中
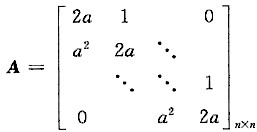
,x=(x
1,…,x
n)
T,b=(1,0,…,0)
T.
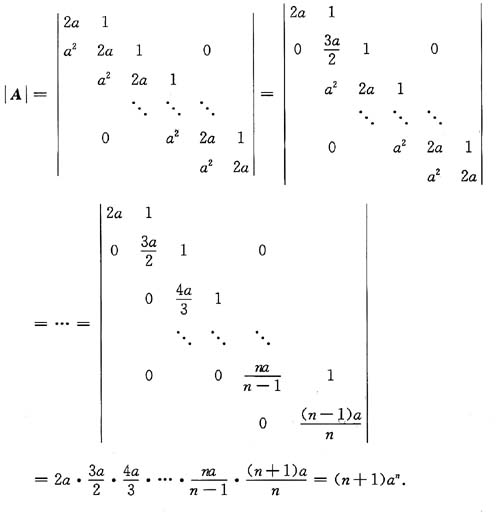
(1)证明行列式|A|=(n+1)a
n.
(2)a为何值时,方程组有唯一解?并求x
1.
(3)a为何值时,方程组有无穷多解?求通解.
利用行列式性质,有
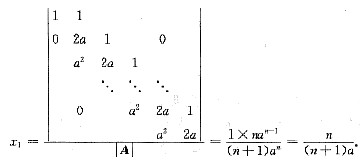
(2) 若方程组Ax=b有唯一解,则|A|=(n+1)a
n≠0,即a≠0.则由克莱姆法则,得
(3) 若使方程组Ax=b有无穷多解,则|A|=(n+1)a
n=0,即a=0.把a=0代入到矩阵A中,显然有r(A┋B)=r(A)=n-1,方程组的基础解系含一个解向量,它的基础解系为k(1,0, 0,…,0)
T(k为任意常数).代入a=0后,方程组化为

特解取(0,1,0,…,0)
T,则方程组Ax=b的通解为k(1,0,0,…,0)
T+(0,1,0,…,0)
T,其中的k为任意常数.
[解析] 线性方程组解的结构和通解.
8. 已知f"(x)<0,f(0)=0,试证:对任意的两个正数x
1和x
2,恒有
f(x
1+x
2)<f(x
1)+f(x
2)
成立.
[详解1] 令F(x)=f(x+x2)-f(x)-f(x2),
则 F'(x)=f'(x+x2)-f'(x)=x2f"(x+θx2)<0 (0<θ<1).
可见,F(x)单调减少.又x1>0,故F(x1)<F(0),
即 f(x1+x2)-f(x1)-f(x2)<0,
也即 f(x1+x2)<f(x1)+f(x2).
[详解2] 不妨设0<x1≤x2,由微分中值定理,有
f(x1)-f(0)=x1f'(ξ1),0<ξ1<x1,
f(x1+x2)-f(x2)=x1f'(ξ2),x2<ξ2<x1+x2.
由题设,f"(x)<0,因此f'(x)单调减少.又ξ1<ξ2,故有f'(ξ2)<f'(ξ1),从而有:f(x1+x2)-f(x2)<f(x1)-f(0).由f(0)=0,得f(x1+x2)<f(x1)+f(x2).
[解析] 本题是不等式证明题,一种考虑是作辅助函数,通过参数变易,比如将x1换为未知变量x,从而得到辅助函数;另一种考虑是,要证的不等式可表示为两点的函数值之差,自然联想到用拉格朗日中值定理进行分析.
9. (1)证明积分中值定理:设f(x)在[a,b]上连续,则存在ξ∈[a,b]使
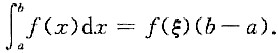
(2)若φ(x)有二阶导数,且满足φ(2)>φ(1),φ(2)>
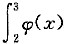
dx出,证明至少存在一点ξ∈(1,3),使得φ"(ξ)<0.
设M和m分别是连续函数f(x)在区间[a,b](b>a)上的最大值和最小值,则有
m(b-a)≤

f(x)dx≤M(b-a).
不等式两边同除以(b-a),得到m
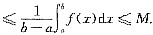
显然
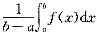
是介于函数f(x)的最大值和最小值之间的.根据闭区间上连续函数的中值定理可知,在区间[a,b]上至少存在一点ξ,使得函数f(x)在该点处的函数值和
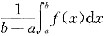
相等,即
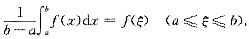
等式两边同乘以(b-a),可得

f(x)dx=(b-a)f(ξ) (a≤ξ≤b).
(2) 由积分中值定理可得,至少存在一点η∈(2,3),使得
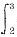
φ(x)dx=φ(η).又φ(2)>

φ(x)dx,所以有
φ(2)>φ(1),φ(2)>φ(η)
因为φ(x)有二阶导数,所以由拉格朗日微分中值定理可知,至少存在一点ξ
1∈(1,2),使得
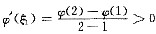
;且至少存在一点ξ
2∈(2,η),使得
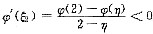
.再由拉格朗日微分中值定理可知,至少存在一点ξ∈(ξ
1,ξ
2),使得
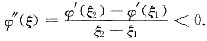
[解析] 积分中值定理.
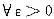 即>0,存在N∈N,当n>N时.有|xn-a|<ε.将此定义与题设所给条件相比较,知两者实质是相同的,因此题设条件也是{xn}收敛于a的充要条件,所以选C.
即>0,存在N∈N,当n>N时.有|xn-a|<ε.将此定义与题设所给条件相比较,知两者实质是相同的,因此题设条件也是{xn}收敛于a的充要条件,所以选C.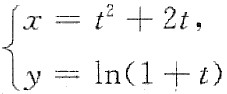 确定,曲线y=y(x)在x=3处的法线与X轴交点的横坐标是______.
确定,曲线y=y(x)在x=3处的法线与X轴交点的横坐标是______. 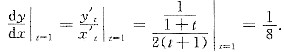
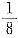 ln2+3.所以选A.
ln2+3.所以选A. f(t2)dt,则F'(x)等于______.
f(t2)dt,则F'(x)等于______. 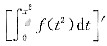 =f[(x2)2]·(x2)'=2xf(x4).
=f[(x2)2]·(x2)'=2xf(x4). 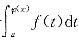 ,其求导公式为
,其求导公式为 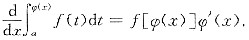
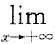 f(x)=0时,必有
f(x)=0时,必有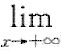 f(x)=0
f(x)=0 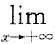 f'(x)存在时,必有
f'(x)存在时,必有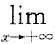 f'(x)=0
f'(x)=0 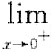 f(x)=0时,必有
f(x)=0时,必有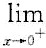 f'(x)=0
f'(x)=0 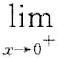 f'(x)存在时,必有
f'(x)存在时,必有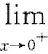 f'(x)=0
f'(x)=0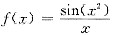 ,则
,则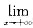 f(x)=
f(x)=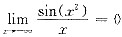 .但
.但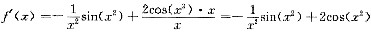 ,其中2cos(x2)项当x→∞时极限不存在,即
,其中2cos(x2)项当x→∞时极限不存在,即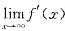 不存在.所以A可排除.
不存在.所以A可排除. 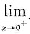 f(x)=0,且
f(x)=0,且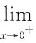 f'(x)=
f'(x)=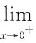 cosx=1.
cosx=1. 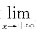 f'(x)存在,记为
f'(x)存在,记为 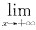 f'(X)=f'(+∞).
f'(X)=f'(+∞). 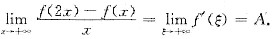
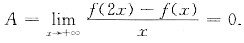
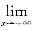 f'(x)=0,综上,选B.
f'(x)=0,综上,选B.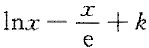 在(0,+∞)内零点的个数为______.
在(0,+∞)内零点的个数为______. 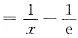 ,令f'(x)=0,得x=e.
,令f'(x)=0,得x=e. 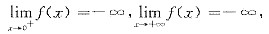
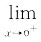 f(x)=-∞,
f(x)=-∞,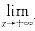 f(x)=-∞是确定零点存在性的重要条件.
f(x)=-∞是确定零点存在性的重要条件.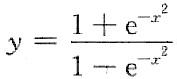 ______.
______. 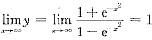 ,所以y=1为其水平渐近线.
,所以y=1为其水平渐近线. 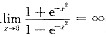 ,所以x=0为其铅直渐近线.
,所以x=0为其铅直渐近线. 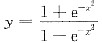 既有水平渐近线又有铅直渐近线,故应选D.
既有水平渐近线又有铅直渐近线,故应选D. 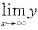 不存在,则应继续考虑
不存在,则应继续考虑 y或
y或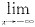 y,其中任何一个存在均说明有水平渐近线(y轴正向或负向);同样对于不连续点x0,若
y,其中任何一个存在均说明有水平渐近线(y轴正向或负向);同样对于不连续点x0,若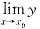 不存在且非无穷大量,则应继续考虑
不存在且非无穷大量,则应继续考虑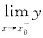 或
或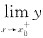 ,其中任何一个为无穷大量.均说明x=x0为铅直渐近线.
,其中任何一个为无穷大量.均说明x=x0为铅直渐近线.
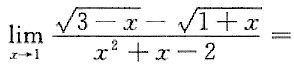 ______.
______.
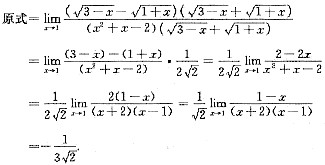
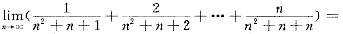 ______.
______.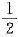
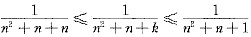 ,
, 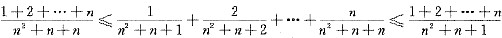 .
. 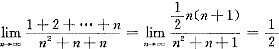 ,
, 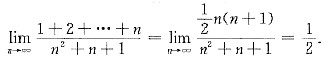
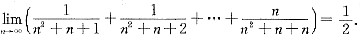
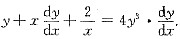
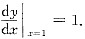
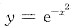 的上凸区间是______.
的上凸区间是______.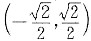
 求一阶、二阶导数,得
求一阶、二阶导数,得 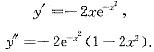
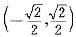 时,曲线向上凸.
时,曲线向上凸.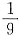 的解为______.
的解为______.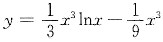
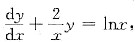
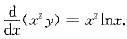
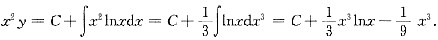
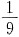 ,得C=0,所以
,得C=0,所以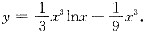
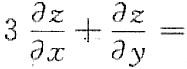 ______.
______.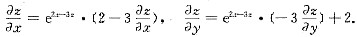
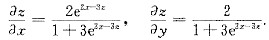
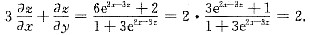
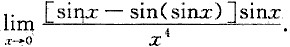 .
.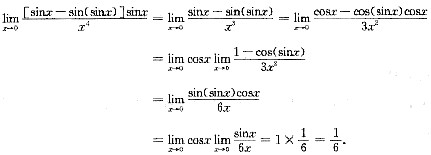
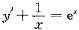 .由一阶线性微分方程的通
.由一阶线性微分方程的通 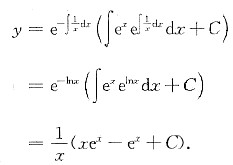

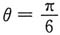 处的切线与法线的直角坐标方程.
处的切线与法线的直角坐标方程.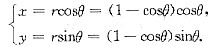
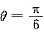 时,
时, 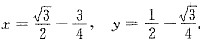
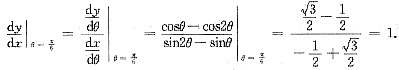
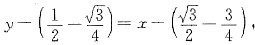
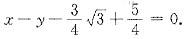
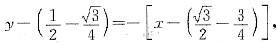
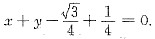
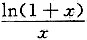 ,计算∫f(x)dx.
,计算∫f(x)dx.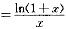 ,因此令t=lnx,即x=e',代入上式得
,因此令t=lnx,即x=e',代入上式得 
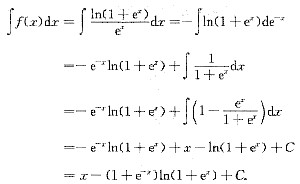
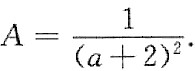
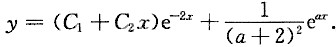
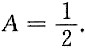
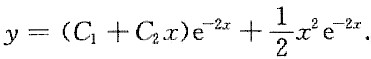
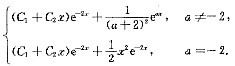
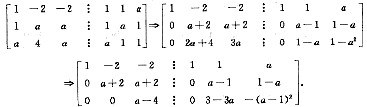
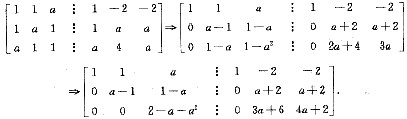
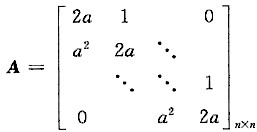 ,x=(x1,…,xn)T,b=(1,0,…,0)T.
,x=(x1,…,xn)T,b=(1,0,…,0)T. 

 特解取(0,1,0,…,0)T,则方程组Ax=b的通解为k(1,0,0,…,0)T+(0,1,0,…,0)T,其中的k为任意常数.
特解取(0,1,0,…,0)T,则方程组Ax=b的通解为k(1,0,0,…,0)T+(0,1,0,…,0)T,其中的k为任意常数.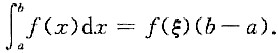
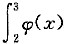 dx出,证明至少存在一点ξ∈(1,3),使得φ"(ξ)<0.
dx出,证明至少存在一点ξ∈(1,3),使得φ"(ξ)<0. f(x)dx≤M(b-a).
f(x)dx≤M(b-a). 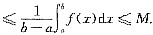 显然
显然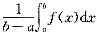 是介于函数f(x)的最大值和最小值之间的.根据闭区间上连续函数的中值定理可知,在区间[a,b]上至少存在一点ξ,使得函数f(x)在该点处的函数值和
是介于函数f(x)的最大值和最小值之间的.根据闭区间上连续函数的中值定理可知,在区间[a,b]上至少存在一点ξ,使得函数f(x)在该点处的函数值和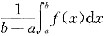 相等,即
相等,即 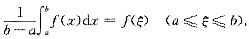
 f(x)dx=(b-a)f(ξ) (a≤ξ≤b).
f(x)dx=(b-a)f(ξ) (a≤ξ≤b). 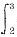 φ(x)dx=φ(η).又φ(2)>
φ(x)dx=φ(η).又φ(2)> φ(x)dx,所以有
φ(x)dx,所以有 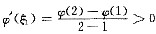 ;且至少存在一点ξ2∈(2,η),使得
;且至少存在一点ξ2∈(2,η),使得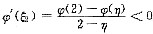 .再由拉格朗日微分中值定理可知,至少存在一点ξ∈(ξ1,ξ2),使得
.再由拉格朗日微分中值定理可知,至少存在一点ξ∈(ξ1,ξ2),使得