一、选择题1. 设f(x)=xsinx+cosx,下列命题中正确的是______.

A B C D
B
[解析] 函数的极大值、极小值.
[解题分析] 因为f(x)在
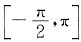
上可导,f'(x)=xcosx>0在区间
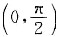
上成立,f'(x)<0在
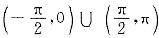
上成立,所以函数f(x)在区间
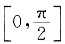
上单调增加,在
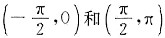
上分别单调递减,所以f(0)是极小值,
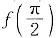
是极大值.故选B.
3. 曲线
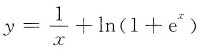 A.0B.1C.2D.3
A.0B.1C.2D.3 A B C D
D
[解析] 渐近线的求法.
[解题分析]
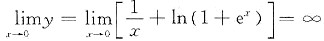
,则x=0是曲线的垂直渐近线;
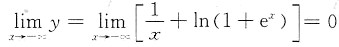
,则y=0是曲线的水平渐近线;
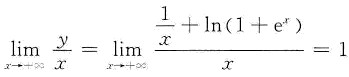
,则y=x是曲线的斜渐近线.
故应选D.
4. 设f(x)=3x
3+x
2|x|,则使f
(n)(0)存在的最高阶数n为______.
A B C D
C
[解析] 分段函数的高阶导数.
[解题分析] 因3x
3处处任意阶可导,只需考查x
2|x|=ψ(x),它是分段函数,x=0是连接点.

又
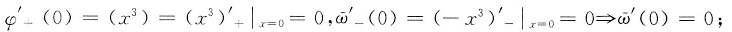
即
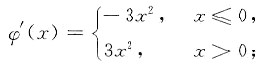
同理可得
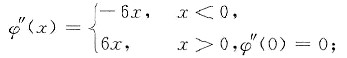
即
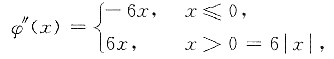
因y=|x|在x=0处不可导
ψ"(0)不存在.应选C.
5. 设f(x)是连续函数,F(x)是f(x)的原函数,则______.
- A.当f(x)是奇函数时,F(x)必为偶函数
- B.当f(x)是偶函数时,F(x)必为奇函数
- C.当f(x)是周期函数时,F(x)必为周期函数
- D.当f(x)是单调增加函数时,F(x)必为单调增函数
A B C D
A
[解析] 函数的单调性、奇偶性.
[解题分析] 排除法.分别举反例如下:
B的反例:取f(x)=cosx.F(x)=sinx+1不是奇函数.
C的反例:取f(x)=cosx+1,F(x)=sinx+x不是周期函数.
D的反例:取f(x)=x,
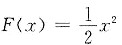
,不是单调增函数.
所以,应选A.
也可以直接证明A正确.f(x)的全体原函数F(x)可表示为
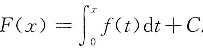
。于是
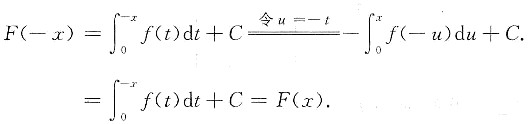
故应选A.
[点评] 设f(x)是(-∞,+∞)上的连续函数,可得如下结论:
(1) 若f(x)是奇函数,则f(x)的每个原函数都是偶函数.
(2) 若f(x)是偶函数,则f(x)有且仅有一个原函数

是奇函数.
(3) 若f(x)是以T>0为周期的周期函数,则f(x)的任一原函数必为一个一次函数与一个以T为周期函数之和;若进一步设
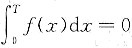
,则f(x)的每个原函数都是以T为周期的周期函数.
6. 设A为反对称矩阵,且|A|≠0,B可逆,A、B为同阶方阵,A
*为A的伴随矩阵,则[A
TA
*(B
-1)
T-1=______.

A B C D
C
[解析] 矩阵的计算.
[解题分析]
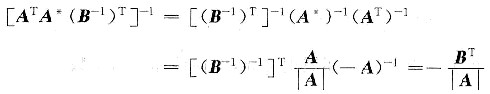
7. 设向量组(Ⅰ)α
1,α
2,…α
s,其秩为r
1,向量组(Ⅱ)β
1,β
2,…,β
s,其秩为r
2,且β
i(i=1,2,…,s)均可以由α
1,…α
s线性表示,则______.
- A.向量组α1+β1,α2+β2,…,αs+βs的秩为r1+r2
- B.向量组α1-β1,α2-β2,…,αs-βs的秩为r1-r2
- C.向量组α1,α2,…,αs,β1,β2,…,βs的秩为r1+r2
- D.向量组α1,α2,…,αs,β1,β2,…,βs的秩为r1
A B C D
D
[解析] 向量组的秩.
[解题分析] 设a
1',a
2',…,
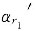
为α
1,α
2,…,α
s的极大线性无关组,则它也是α
1,α
2,…,α
s,β
1,β
2,…,β
s的极大线性无关组,所以D结论成立.
8. 设n个随机变量X
1,X
2.…,X
n独立同分布.且
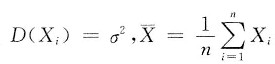
,S
2=
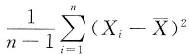
A.S是σ的无偏估计量 B.S是σ的最大似然估计量
C.S是σ的一致估计量 D.S与
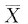
相互独立
A B C D
C
[解析] 随机变量的无偏估计量.
[解题分析] 因为
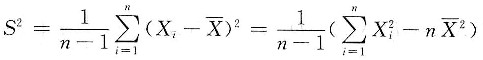
由辛钦大数定律可知
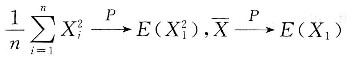
根据依概率收敛的性质可知
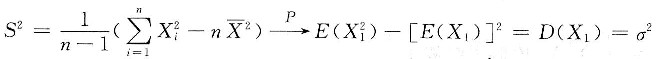
所以
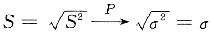
故选C.
二、填空题1. 设矩阵
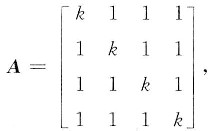
且秩r(A)=3,则k=______.
-3
[解析] 矩阵的秩.
[解题分析] 由题设r(A)=3,则|A|=0,即
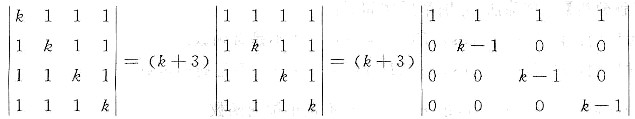
从而k=-3或k=1.当k=1时,

则r(A)=1,与已知矛盾,所以k=-3.
2. 设随机变量X和Y的相关系数为0.9,若Z=X-0.4,则Y与Z的相关系数为______.
0.9
[解析] 相关系数.
[解题分析] 本题考查相关系数的定义,由题设,D(Z)=D(X),
cov(Z,Y)=cov(X-0.4,Y)=E[(X-0.4-E(X-0.4))(Y-E(Y))]
=E[(X-E(X))(Y-E(Y))]=cov(X,Y),
因此
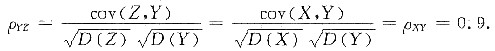
3. 设函数f(x)在x=2的某邻域内可导,且f'(x)=e
f(x),f(2)=1,则f"(2)=______.
2e3
[解析] 一元复合函数求导法则.
[解题分析] 已知f(x)在x=2的某邻域内可导,且f'(x)=ef(x),所以f'(x)在x=2的同一邻域内可导,即在该邻域内函数.f(x)二阶可导,且
f"(x)=[ef(x)'=f'(x)ef(x)=e2f(x).
于是f"(x)也在x=2的同一邻域内可导,即在该邻域内函数f(x)三阶可导,且
f'"(x)=[e2f(x)'=2f'(x)e2f(x)=2e3f(x).
将f(2)=1代入可得f'"(2)=2e3.
4. 设总体X服从参数为2的指数分布,X
1,X
2,…,X
n为来自总体X的简单随机样本,则当n→∞时,
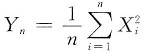
依概率收敛于______.
[解析] 大数定律.
[解题分析] 由题设,X
1,X
2,…,X
n独立同分布,从而

也独立同分布,且
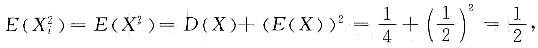
由此
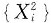
服从大数定律,即
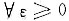
,
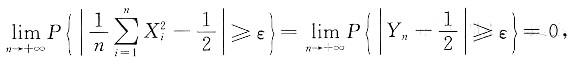
因此
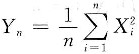
依概率收敛于
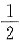
。
5. 设
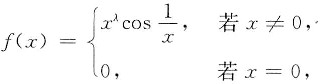
其导函数在x=0处连续,则λ的取值范围是______.
λ>2
[解析] 导数的连续性.
[解题分析] 由题设。当x≠0时,
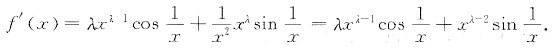
当x=0时,
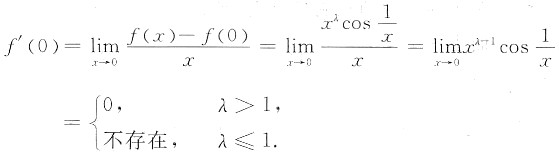
又
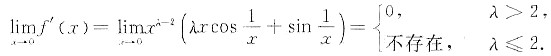
因此,当λ>2时,
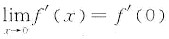
,即f'(x)在x=0处连续.所以λ的取值范围是λ>2.
6. 设行向量组(2,1,1,1),(2,1,a,a),(3,2,1,a),(4,3,2,1)线性相关,且a≠1,则a=______.
[解析] 向量组的线性相关性.
[解题分析] n个n维向量线性相关
|α
1,α
2…α
n|=0.根据题意有
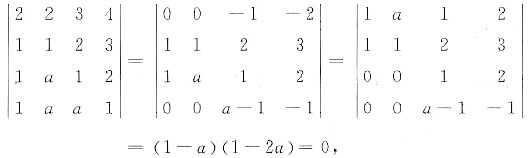
因为a≠1,所以
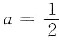
。
三、解答题1. 设A为n阶矩阵,λ
1和λ
2是A的两个不同的特征值,x
1.x
2是分别属于λ
1和λ
2的特征向量.试证明:x
1+x
2不是A的特征向量.
设x1+x2是A的属于某个特征值λ的特征向量.则
A(x1+x2)=λ(x1+x2).
由已知,
Ax1=λ1x1,Ax2=λ2x2,λ1≠λ2,
所以A(x1+x2)=Ax1+Ax2=λ1x1+λ2x2,
于是λ1x1+λ2x2=λ(x1+x2),
从而(λ1-λ)x1+(λ2-λ)x2=0
即λ1=λ2,这与假设矛盾.
所以x1+x2不是A的特征向量.
[解析] 可用反证法,涉及抽象矩阵的特征值、特征向量的问题时往往从定义着手分析.
[评注] 这种否定论述的命题往往用反证法证明是最方便的.
2. 设随机变量X与Y相互独立,X的概率分布为
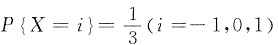
,Y的概率密度为
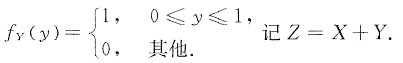
(Ⅰ) 求P{z≤1/2|X=0};
(Ⅱ) 求Z的概率密度.
因为Z=X+Y.所以
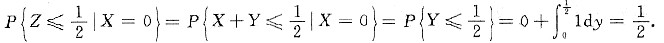
(Ⅱ) 因为Z=X+Y,故随机变量Z的分布函数
F(z)=P{Z≤z}=P{X+Y≤z}.
显然当z≥2时,X,Y的所有取值均满足上式,即F(z)=1;相反当z<-1时,X,Y只能取空值,则有F(z)=0;而当-1≤z<2时,
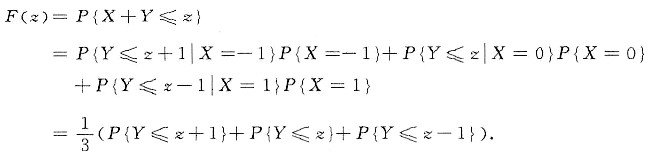
当-1≤z<0时,
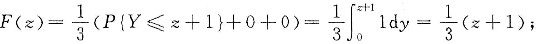
当0≤z<1时,
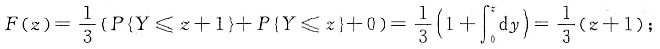
当1≤z<2时,
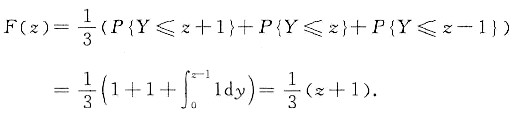
故可得到随机变量Z的分布函数和概率密度分别为
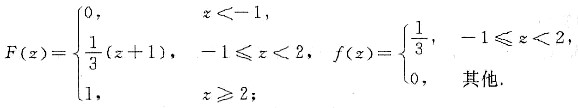
[解析] 随机变量的条件概率与概率密度.
3. 设矩阵A与B相似,其中
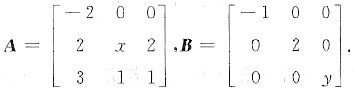
(1) 求x与y的值;
(2) 求可逆矩阵P,使得P
-1AP=B.
(1) 因为A与B相似,故其特征多项式相同,即
|λE-A|=|λE-B|,
(λ+2)[λ
2-(x+1)λ+(x-2)]=(λ+1)(λ-2)(λ-y),
令λ=0,得2(x-2)=2y,即y=x-2,
令λ=1,得y=-2,从而x=0.
(2)由(1)知
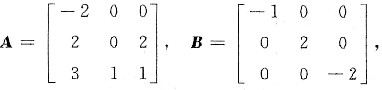
对应于A的特征值-1、2、-2的特征向量分别为
ξ
1=(0,2,-1)
T,ξ
2=(0,1,1)
T,ξ
3=(1,0,-1)
T,
则可逆矩阵

,满足P
-1AP=B.
[解析] 由此可定出参数x,y.若A与B相似,则|λE-A|=|λE-B|对所有λ均成立.
[评注] 若A与B相似,则有|λE-A|=|λE-B|,|A|=|B|,r(A)=r(B),一般由以上三个等式求出A、B中所含的未知参数.
4. 设函数f(x)在[0,3]上连续,在(0,3)内可导,且f(0)+f(1)+f(2)=3,f(3)=1,试证必存在ξ∈(0,3),使f'(ξ)=0.
由题设,f(x)在[0,3]上连续,则f(x)在[0,2]上也必然连续,则在[0,2]上f(x)必有最大值M和最小值m,因而m≤f(0)≤M,m≤f(1)≤M,m≤f(2)≤M,从而
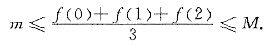
由连续函数的介值定理,知存在一点η∈[0,2],使
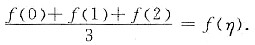
由已知条件f(0)+f(1)+f(2)=3,可推知f(η)=1,因此
f(η)=f(3)=1,η∈[0,2].
由罗尔定理,知存在
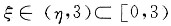
,使f'(ξ)=0.证毕.
[解析] 介值定理、微分中值定理.
5. 设某酒厂有一批新酿的好酒,如果现在(假定t=0)就售出,总收入为R
0(元).如果窑藏起来待来日按陈酒价格出售,t年末总收入为

假定银行的年利率为r,并以连续复利计算,试求窑藏多少年售出可使总收入的现值最大,并求r=0.06时的t值.
由题设,知年利率为r,则由连续复利公式,现时本金A元,则到t年时本金利息合计应为R(t)=Ae
n,因此要使t年时本金利息合计为R(t),则现时本金应为A(t)=R(t)e
-n,已知这批酒窖藏t年末售出总收入R的现值为A(t)=Re
-rt,又已知
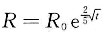
,从而
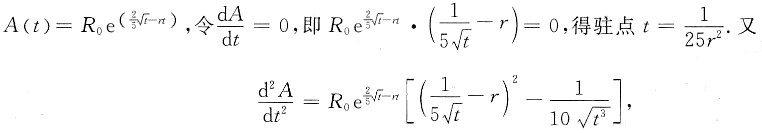
且
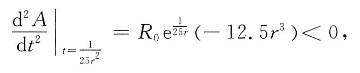
所以
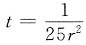
是A的极大值点,从而也就是最大值点,即应窖藏
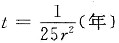
售出,
当r=0.06时,
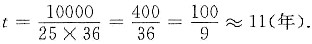
[解析] 一元函数的最值.
6. 已知连续函数f(x)满足条件

,求f(x).
方程
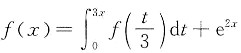
两边对x求导得
f'(x)=3f(x)+2e
2x,即f'(x)-3f(x)=2e
2x,
令x=0,由原方程得f(0)=1.
于是,原问题就转化为求微分方程f'(x)-3f(x)=2e
2x满足初始条件f(x)=1的特解.
由一阶线性微分方程的通解公式,得
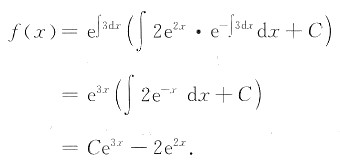
代入初始条件f(0)=1,得C=3,
从而f(x)=3e
3x-2e
2x.
[解析] 先在等式两边对x求导,消去变限积分,将原方程化为关于未知函数f(x)的微分方程,再求解该微分方程.
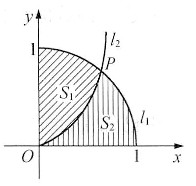
7. 假设曲线l
1:y=1-x
2(0≤x≤1)与x轴、y轴所围成区域被曲线l
2:y=ax
2分为面积相等的两部分,其中a是大于零的常数,试确定a的值.
如图,由
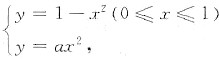
得曲线l
1与曲线l
2的交点为
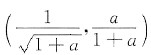
,所求平面图形面积为
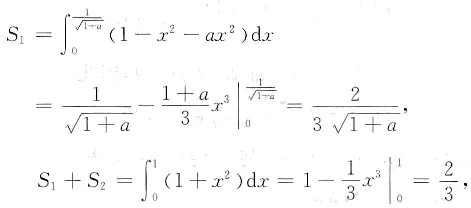
因为S
1=S
2,所以
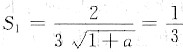
,得a=3.
[解析] 先求出曲线l1与曲线l2的交点,然后利用定积分求平面图形面积的公式计算出S1和S2.由S1=S2求a的值.
[评注] 本题是利用定积分求面积的基本题型,只是以反问题的形式出现,即已知面积的关系反求参数a,这种出题方式应引起注意.
8. 设矩阵
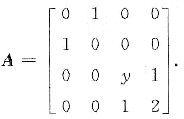
(1) 已知A的一个特征值为3,试求y;
(2)求矩阵P,使(AP)
T(AP)为对角矩阵.
(1) 因为

当λ=3时,代入上式解得y=2.于是

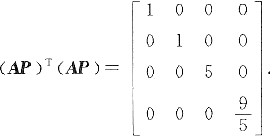
(2) 方法一 由A
T=A,得(AP)
T(AP)=P
TA
2P,
而矩阵

考虑二次型

令y
1=x
1,y
2=x
2.
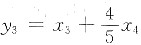
,y
4=x
4,得

取

则有
方法二 先求出A
2的特征值λ
1=1(三重),λ
2=9.
对应于λ
1=1的特征向量为
α
1=(1,0,0,0)
T,α
2=(0,1,0,0)
T,α
3=(0,0,-1,1)
T.
经正交并单位化后,得向量组β
1=(1,0,0,0)
T,β
2=(0,1,0,0)
T 对应于λ
2=9的特征向量为α
4=(0,0,1,1,)
T,经单位化后,得
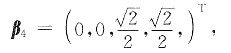
令
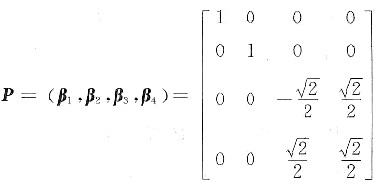
则
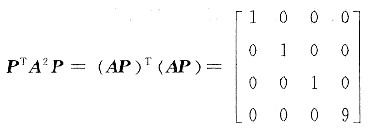
[解析] 由定义有|3E-A|=0,由此可定出参数y.考虑到A2为对称矩阵,而(AP)T(AP)=PTA2P,化其对角矩阵方法有两种:转化为对应二次型xTA2x,通过非退化线性变换x=Py化为标准形,相应求出P;或者求出A2的特征值、单位化,最后构造出正交矩阵P,本题所求P不唯一.
[评注] 将一个实对称矩阵化为对角阵可用二次型的配方法也可用正交变换法,但两者是有本质区别的.用配方法得到的对角阵的对角线上的元素不一定是矩阵特征值,得到的可逆矩阵P也不一定是正交的,而正交变换法得到的对角线上的元素一定是矩阵特值,得到可逆矩阵P也一定是正交的.
9. 一台设备由三大部分构成,在设备运转中各部件需要调整的概率相应为0.10、0.20和0.30.假设各部件的状态相互独立,以X表示同时需要调整的部件数.试求X的概率分布、数学期望E(X)和方差D(X).
[详解1] 设事件A
i={部件i需要调整},i=1,2,3.则A
1,A
2,A
3相互独立,并有
P(A
1)=0.1,P(A
2)=0.2,P(A
3)=0.3.
由题意知,X的所有可能取值为0,1,2,3.且
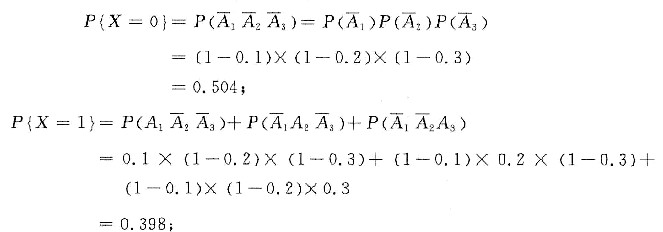
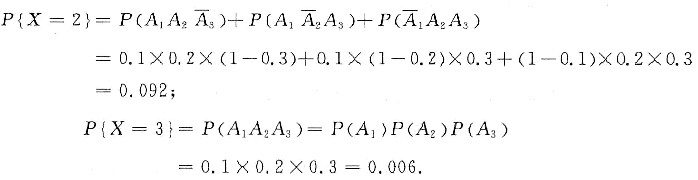
即X的概率分布为
X |
0 |
1 |
2 |
3 |
P |
0.504 |
0.398 |
0.092 |
0.006 |
因此X的数学期望
E(X)=0×P{X=0}+1×P{X=1}+2×P{X=2}+3×P{X=3}
=0×0.504+1×0.398+2×0.092+3×0.006
=0.6.
又因为E(X
2)=0
2×P{X=0}+1
2×P{X=1)+2
2×P{X=2}+3
2×P{X=3}
=0×0.504+1×0.398+4×0.092+9×0.006
=0.82.
所以X的方差
D(X)=E(X
2)-[E(X)]
2=0.82-0.6
2=0.46.
[详解2] 设
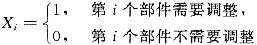
,i=1,2,3.则X
1,X
2,X
3相互独立,且X
1,X
2.X
3分别服从参数为0.1,0.2,0.3的0-1分布.即:
由题设知,X=X
1+X
2+X
3,显然X的所有可能取值为0,1,2,3.且
P{X=0}=P{X
1=0,X
2=0,X
3=0}=P{X
1=0}P{X
2=0}P{X
3=0}
=0.9×0.8×0.7=0.504;
P{X=3}=P{X
1=1,X
2=1,X
3=1}=P{X
1=1}P{X
2-1}P{X
3=1}
=0.1×0.2×0.3=0.006;
P{X=1}=P{X
1=1,X
2=0,X
3=0}+P{X
1=0,X
2=1,X
3=0}+P{X
1=0,
X
2=0,X
3=1}
=0.1×0.8×0.7+0.9×0.2×0.7+0.9×0.8×0.3=0.398;
P{X=2}=1-P{X=0}-P{X=1}-P{X=3}
=1-0.504-0.398-0.006=0.092.
因此X的概率分布为
X |
0 |
1 |
2 |
3 |
P |
0.504 |
0.398 |
0.092 |
0.006 |
因为X
i均服从0-1分布,所以
E(X
1)=0.1,E(X
2)=0.2,E(X
3)=0.3,
D(X
1)=0.1×0.9=0.09,D(X
2)=0.2×0.8=0.16,D(X
3)=0.3×0.7=0.21.
于是E(X)=E(X
1+X
2+X
3)=E(X
1)+E(X
2)+E(X
3)=0.6.
D(X)=D(X
1+X
2+X
3)=D(X
1)+D(X
2)+D(X
3)=0.46.
[解析] 先确定X的所有可能取值,然后分别求出每一取值的概率,再按定义求数学期望和方差即可.
[评注] 详解1思路直观,容易想到;详解2借助独立性及其运算性质,思路巧妙.

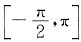 上可导,f'(x)=xcosx>0在区间
上可导,f'(x)=xcosx>0在区间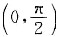 上成立,f'(x)<0在
上成立,f'(x)<0在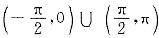 上成立,所以函数f(x)在区间
上成立,所以函数f(x)在区间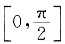 上单调增加,在
上单调增加,在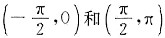 上分别单调递减,所以f(0)是极小值,
上分别单调递减,所以f(0)是极小值,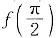 是极大值.故选B.
是极大值.故选B.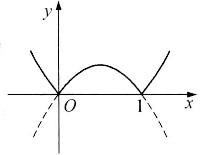
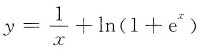
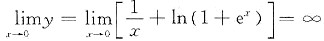 ,则x=0是曲线的垂直渐近线;
,则x=0是曲线的垂直渐近线;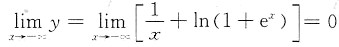 ,则y=0是曲线的水平渐近线;
,则y=0是曲线的水平渐近线;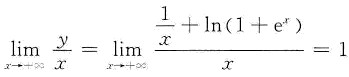 ,则y=x是曲线的斜渐近线.
,则y=x是曲线的斜渐近线.
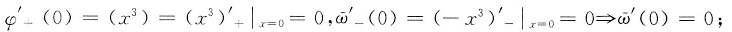
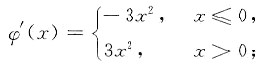
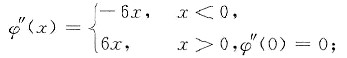
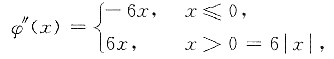
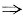 ψ"(0)不存在.应选C.
ψ"(0)不存在.应选C.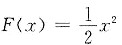 ,不是单调增函数.
,不是单调增函数.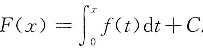 。于是
。于是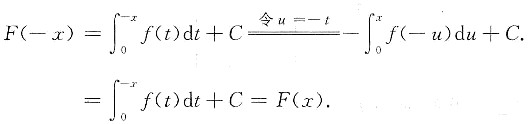
 是奇函数.
是奇函数.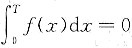 ,则f(x)的每个原函数都是以T为周期的周期函数.
,则f(x)的每个原函数都是以T为周期的周期函数.
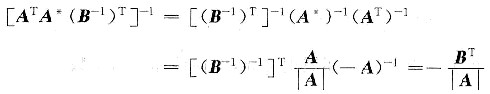
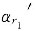 为α1,α2,…,αs的极大线性无关组,则它也是α1,α2,…,αs,β1,β2,…,βs的极大线性无关组,所以D结论成立.
为α1,α2,…,αs的极大线性无关组,则它也是α1,α2,…,αs,β1,β2,…,βs的极大线性无关组,所以D结论成立.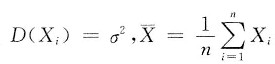 ,S2=
,S2=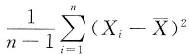 A.S是σ的无偏估计量 B.S是σ的最大似然估计量
A.S是σ的无偏估计量 B.S是σ的最大似然估计量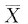 相互独立
相互独立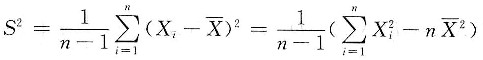
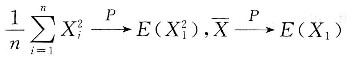
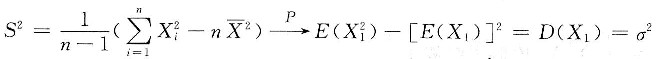
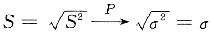

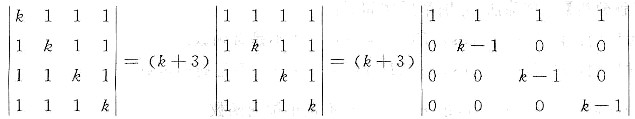

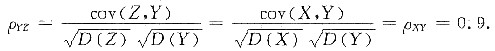
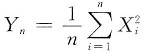 依概率收敛于______.
依概率收敛于______.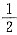
 也独立同分布,且
也独立同分布,且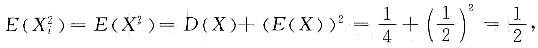
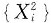 服从大数定律,即
服从大数定律,即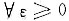 ,
,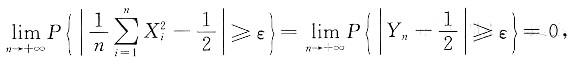
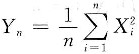 依概率收敛于
依概率收敛于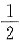 。
。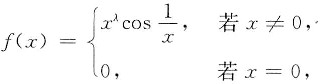 其导函数在x=0处连续,则λ的取值范围是______.
其导函数在x=0处连续,则λ的取值范围是______.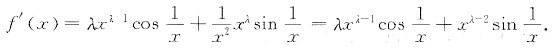
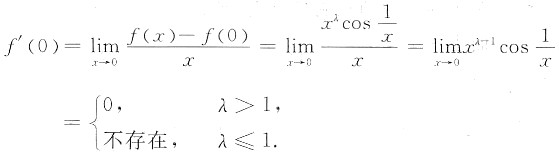
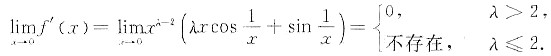
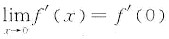 ,即f'(x)在x=0处连续.所以λ的取值范围是λ>2.
,即f'(x)在x=0处连续.所以λ的取值范围是λ>2.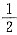
 |α1,α2…αn|=0.根据题意有
|α1,α2…αn|=0.根据题意有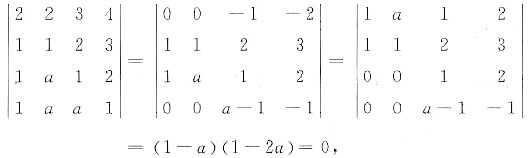
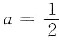 。
。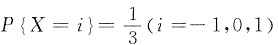 ,Y的概率密度为
,Y的概率密度为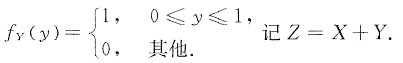
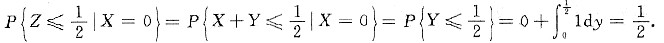
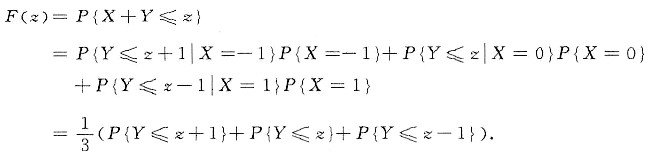
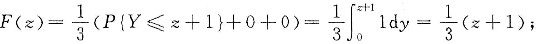
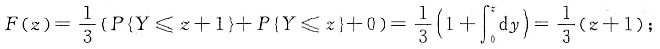
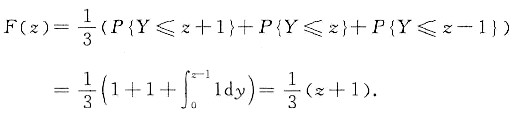
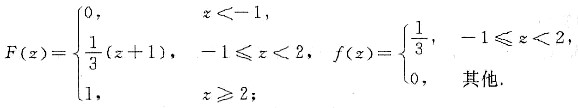
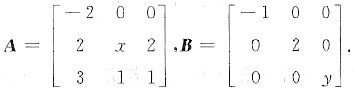
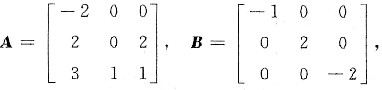
 ,满足P-1AP=B.
,满足P-1AP=B.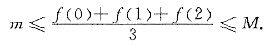
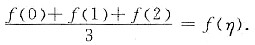
 ,使f'(ξ)=0.证毕.
,使f'(ξ)=0.证毕.
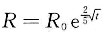 ,从而
,从而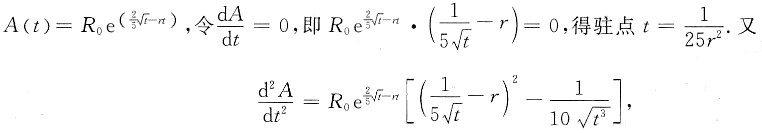
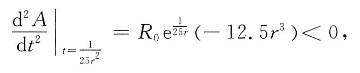
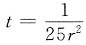 是A的极大值点,从而也就是最大值点,即应窖藏
是A的极大值点,从而也就是最大值点,即应窖藏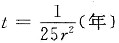 售出,
售出,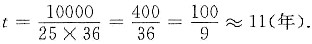
 ,求f(x).
,求f(x).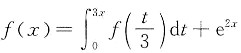 两边对x求导得
两边对x求导得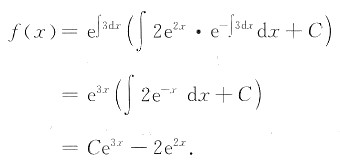
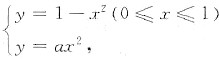 得曲线l1与曲线l2的交点为
得曲线l1与曲线l2的交点为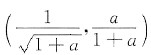 ,所求平面图形面积为
,所求平面图形面积为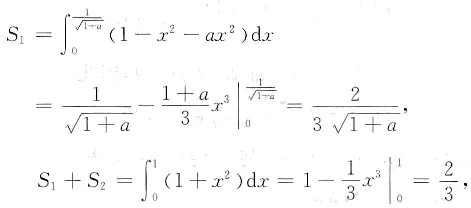
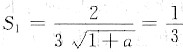 ,得a=3.
,得a=3.
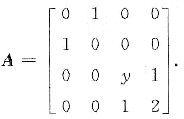




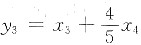 ,y4=x4,得
,y4=x4,得


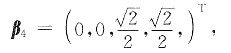
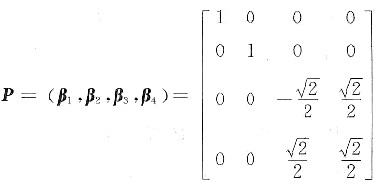
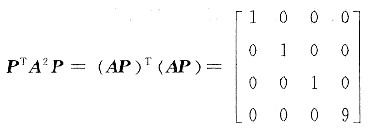
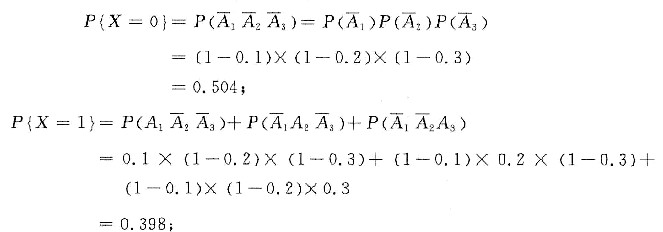
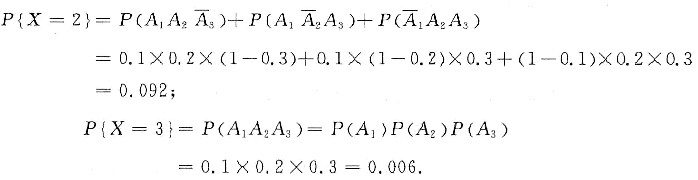
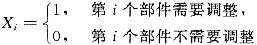 ,i=1,2,3.则X1,X2,X3相互独立,且X1,X2.X3分别服从参数为0.1,0.2,0.3的0-1分布.即:
,i=1,2,3.则X1,X2,X3相互独立,且X1,X2.X3分别服从参数为0.1,0.2,0.3的0-1分布.即:
