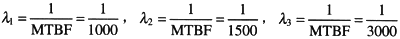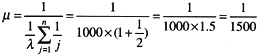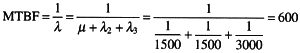1. 三个可靠度只均为0.8的部件串联构成一个系统,如图3-1所示。

则该系统的可靠度为
。
- A.0.240
- B.0.512
- C.0.800
- D.0.992
A B C D
B
[解析]
计算机系统是一个复杂的系统,而且影响其可靠性的因素也非常繁复,很难直接对其进行可靠性分析;但通过建立适当的数学模型,把大系统分割成若干子系统,可以简化其分析过程。常见的系统可靠性数学模型有以下三种。
1.串联系统
假设一个系统由n个子系统组成,当且仅当所有的子系统都能正常工作时,系统才能正常工作,这种系统称为串联系统,如图3-2所示。

设系统各个子系统的可靠性分别用R
1,R
2,…,R
n表示,则系统的可靠性为:
R=R
1×R
2×…×R
n 如果系统的各个子系统的失效率分别用λ
1,λ
2,…,λ
n来表示,则系统的失效率为:
λ=λ
1+λ
2+…+λ
n 2.并联系统
假如一个系统由n个子系统组成,只要有一个子系统能够正常工作,系统就能正常工作,这种系统称为并联系统,如图3-3所示。
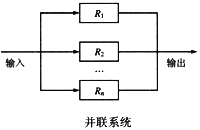
设系统各个子系统的可靠性分别用R
1,R
2,…,R
n表示,则系统的可靠性为
R=1-(1-R
1)×(1-R
2)×…×(1-R
n)
假如所有的子系统的失效率均为l则系统的失效率为:
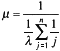
在并联系统中只有一个子系统是真正需要的,其余n-1个子系统称为冗余子系统,随着冗余子系统数量的增加,系统的平均无故障时间也增加了。
3.模冗余系统
m模冗余系统由m个(m=2n+1,为奇数)相同的子系统和一个表决器组成,经过表决器表决后,m个子系统中占多数相同结果的输出作为系统的输出,如图3-4所示。
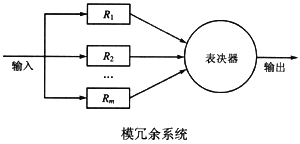
在m个子系统中,只有n+1个或n+1个以上子系统能正常工作,系统就能正常工作,输出正确结果。假设表决器是完全可靠的,每个子系统的可靠性为R
0,则m模冗余系统的可靠性为:
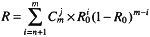
其中
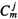
为从m个元素中取j个元素的组合数。
显然,本题是一个简单的串联系统可靠性计算的试题,其可靠性为
R=0.8×0.8×0.8=0.512
表3-1 各类指令的平均指令周期和使用频度 指令类别 | 平均机器周期数/指令 | 使用频度 |
访内存 | 2.5 | 25% |
一般算术逻辑运算 | 1.25 | 40% |
比较与转移等 | 1.5 | 25% |
乘除 | 15 | 5% |
其他 | 5 | 5% |
若某项事务处理工作所要执行的机器指令数是:控制程序(以访问内存、比较与转移等、其他指令为主)220000条指令和业务程序(以包括乘除在内的算术逻辑运算为主)90000条指令,旦指令使用频度基本如表3-1所示,则该计算机系统的事务处理能力约为 (6) 项/秒。若其他条件不变,仅提高主振频率至150MHz,则此时该计算机速度平均约为 (7) 兆条指令/秒,对上述事务的处理能力约为 (8) 项/秒。若主频仍为100MHz,但由于采用了流水线和专用硬件等措施,使各类指令的每条指令平均机器周期数都变为1.25,此时,计算机的速度平均约为 (9) 兆条指令/秒。 分别考虑如图3-6的a,b,c和d所示的系统。若其中单个I/O的可靠性都是R1,单个CPU的可靠性都是R2,单个MEM的可靠性都是R3,而三选二表决器的可靠性为1,则图a系统的可靠性为 10 ,图b系统的可靠性为 11 ,图c系统的可靠性为 12 ,图d系统的可靠性为 13 。
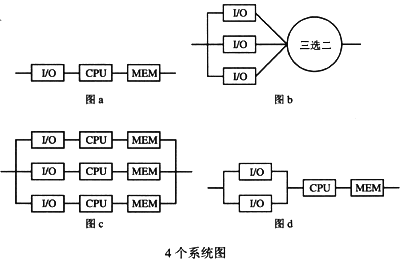
对于如图3-6所示的d所示系统,若单个I/O,CPU和MEM的平均无故障间隔时间 (MTBF)分别为1000小时、1500小时和3000小时,则系统的MTBF为 14 小时。14.
A B C D
B
[解析]
图3-6(a)中,I/O、CPU和MEM三者是串联的,根据3.1.1节中的串联系统模型公式,得到图3-6(a)系统的可靠性为:
R=R
1×R
2×R
3 图3-6(b)是冗余系统模型。在一个有m=2n+1个子系统的冗余系统中,只要有 n+1个或n+1个以上子系统能正常工作,系统就能正常工作,输出正确结果。现在我们用题目给出的数据代入到3.1.1节中的冗余系统模型公式,则n+1=2,m=3。图3-6(b)系统的可靠性为:
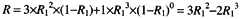
图3-6(c)为先串联再并联,I/O,CPU,MEM串联的可靠性前面已经求得为 R
1×R
2×R
3。现把它们看成一个整体,进行并联。把题目数据代入到3.1.1节中的并联系统模型公式,得到图3-6(c)系统的可靠性为:
R=1-(1-R
1×R
2×R
3)
3 图3-6(d)为先并联再串联,两个I/O系统并联的可靠性为1-(1-R
1)
2。再把它与 CPU和MEM进行串联得图3-6(d)系统的可靠性为:
[1-(1-R
1)
2]×R
2×R
3=(1-(1-2R
1+
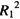
))×R
2×R
3=(2-R
1)×R
1×R
2×R
3 接下来是求MTBF,MTBF是系统的平均无故障时间。由于平均无故障时间MTBF与失效率A之间有关系:MTBF=
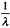
,则根据题目中的条件,有
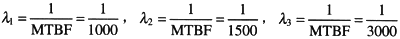
图3-6(d)的前半部分是两个I/O系统并联,根据第1题中的并联系统失效率公式,可得:
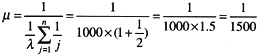
因此,根据第1题中的串联系统的失效率公式,整个图3-6(d)系统的MTBF为:
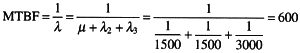
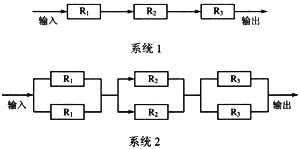
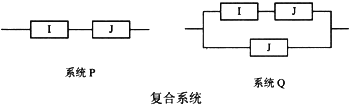 设在图3-8和图3-9所示的系统中,R1,R2,R3为3个加工部件,每个加工部件的失效率均为丸,可靠性均为只。则图3-8系统的失效率为 20 ,可靠性为 21 。图3-9中系统的失效率为 22 ,可靠性为 23 。若每个加工部件的平均无故障时间为5000小时,则图3-9中系统的平均无故障时间为 24 小时。
设在图3-8和图3-9所示的系统中,R1,R2,R3为3个加工部件,每个加工部件的失效率均为丸,可靠性均为只。则图3-8系统的失效率为 20 ,可靠性为 21 。图3-9中系统的失效率为 22 ,可靠性为 23 。若每个加工部件的平均无故障时间为5000小时,则图3-9中系统的平均无故障时间为 24 小时。
 发展容错技术可提高计算机系统的可靠性。利用元件冗余可保证在局部有故障的情况下系统正常工作。带有热备份的系统称为 25 系统。它是 26 ,因此只要有一个子系统能正常工作,整个系统仍能正常工作。
发展容错技术可提高计算机系统的可靠性。利用元件冗余可保证在局部有故障的情况下系统正常工作。带有热备份的系统称为 25 系统。它是 26 ,因此只要有一个子系统能正常工作,整个系统仍能正常工作。


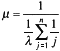

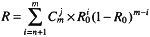
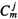 为从m个元素中取j个元素的组合数。
为从m个元素中取j个元素的组合数。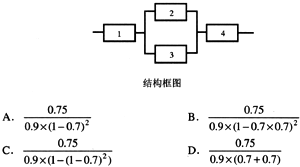

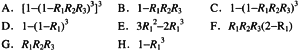
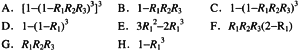
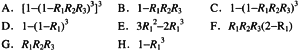
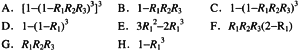
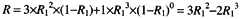
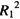 ))×R2×R3=(2-R1)×R1×R2×R3
))×R2×R3=(2-R1)×R1×R2×R3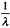 ,则根据题目中的条件,有
,则根据题目中的条件,有