第一部分 常识判断根据题目要求,在四个选项中选出一个最恰当的答案。9. 歌曲是时代的产物,下列歌词按反映的时代先后排序,正确的是:______
①打倒列强!打倒列强!除军阀!除军阀!
②我的家在东北松花江上……从那个悲惨的时候,脱离了我的家乡
③雄赳赳,气昂昂,跨过鸭绿江。保和平,为祖国,就是保家乡
④如今的南泥湾,与往年不一般……是陕北的好江南
⑤驱除鞑虏,还我中华!铁血男儿壮志冲九霄
- A.②①③⑤④
- B.④①⑤②③
- C.③①⑤④②
- D.⑤①②④③
A B C D
D
[解析] ①歌词出自《国民革命歌》。1925年2月20日,《国民革命歌》在《中国军人》创刊号上刊登,由黄埔军人创作词曲。该歌出现后广为传唱,反映了在国民革命时期,广东革命根据地民众“打倒列强,除军阀”的愿望。
②歌词出自《松花江上》。《松花江上》是1935年张寒晖在西安目睹东北军和东北人民流亡惨状而创作的一首抗日歌曲。歌曲唱出了“九一八”事变(1931年)后东北民众以至中国人民的悲愤情怀。
③歌词出自《中国人民志愿军战歌》。《中国人民志愿军战歌》创作于1950年,由麻扶摇作词、周巍峙作曲,反映了中华人民共和国成立初期中国人民志愿军抗美援朝(1950—1953年)的决心。
④歌词出自《南泥湾》。《南泥湾》由贺敬之写于1943年,反映了20世纪40年代初南泥湾经过大生产运动后发生的翻天覆地的巨大变化。
⑤歌词出自《辛亥首义歌》。《辛亥首义歌》创作于武昌起义后不久,反映的是发生于1911年的武昌起义。选项中歌词按反映的时代先后排序,正确的是⑤①②④③。
故本题选D。
第二部分 言语理解与表达本部分包括表达与理解两方面的内容。请根据题目要求,在四个选项中选出一个最恰当的答案。26. ①交通的高速发展使人们感觉生活在“地球村”,空间成为虚拟符号或只意味着数字的变化
②正如有人指出的,“在城市消费时代,艺术的接受者与创造者都趋向于职业化”
③民俗是在特定地理环境下产生有明显地域性的文化,当地方性消弭时民俗也随之消失
④大众传播媒介使时空缩小,网络瞬时传播的速度和广度超越以往任何时候
⑤即由于地理气候等因素长期养成的生存智慧失去了优势,地方文化的多样性也不复存在了
⑥一些传统民俗在当代被商家和政府征用,变成了量贩式的“工业产品”
将以上6个句子重新排列,语序正确的是:______
- A.④⑤③①②⑥
- B.⑥⑤③②①④
- C.③⑤④①⑥②
- D.①⑤⑥②④③
A B C D
C
[解析] 本题从首句入手较难做出判断。通读题干所给句子,发现⑤以“即”开头,应是对其前一句内容的解释说明。⑤指出长期养成的生存智慧失去了优势,地方文化的多样性也不复存在了,与之对应的只能是③中的“当地方性消弭时民俗也随之消失”,故③⑤应前后相连,排除A、B、D。
验证C项,首先③⑤引出“民俗”的话题,并指出民俗随地方性消弭而消失;然后④①提出大众传播媒介、交通的高度发展使得时空缩小,地域性差异逐渐消失;⑥指出一些传统民俗在当代的发展过程中变成了量贩式的“工业产品”;②中的“职业化”对⑥中的“量贩式的‘工业产品’”进一步说明,逻辑无误。
故本题选C。
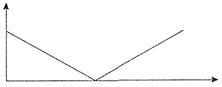
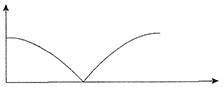
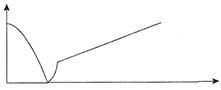
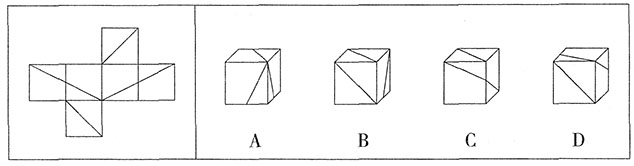
第三部分 数量关系在这部分试题中,每道题呈现一段表述数字关系的文字,要求你迅速、准确地计算出答案。2. 甲、乙两辆小车从相距100米的轨道两端同时出发相向而行,甲车以2米/秒的速度匀速行驶,乙车从静止状态开始以1米/秒
2的加速度均匀加速行驶,到达终点后停下,问:以下哪个图能准确描述甲、乙各自到达终点前,两车之间的距离与时间的关系(横轴为时间,纵轴为直线距离)?______
A.
B.
C.

D.
A B C D
D
[解析] 根据s=vt,可知甲行驶到终点所用时间
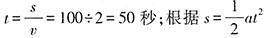
,可知乙行驶到终点所用时间
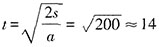
秒,乙比甲先到达终点,故该运动过程可分为三个阶段,即两车相遇前、相遇后和乙到达终点后。
设两车的行驶时间为t,两车之间的距离为s。①甲、乙两车相遇之前,两车之间的距离等于轨道长减去两车的行驶路程,那么
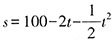
,是开口朝下的抛物线;②甲、乙两车相遇之后,背向而行,两车之间的距离等于两车的行驶路程之和减去轨道长,那么
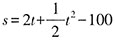
,是开口朝上的抛物线;③乙车到达终点后,甲车继续行驶,此时两车之间的距离即甲车的行驶路程,那么s=2t,是一元一次函数。故本题选D。
[备注:已知该运动过程分为三个阶段,选项中只有D项的函数图象分三段,可直接确定选D。]
3. 甲、乙两个箱子中分别装有不同数量的某种商品,总数不到100件。如果从甲箱或乙箱中随机拿出1件这种商品,拿到次品的概率分别为5%和10%。如果将两箱内的商品混合后再随机拿出1件,则拿到次品的概率为6%。问:从乙箱中随机拿出3件这种商品,均不为次品的概率x在以下哪个范围内?______
- A.x<72%
- B.72%≤x<81%
- C.81%≤x<90%
- D.x≥90%
A B C D
A
[解析] 方法一,根据题意可知,随机拿出一件商品是次品的
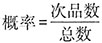
。设甲、乙两箱商品的数量分别为a、b,可列方程5%a+10%b=6%×(a+b),化简得到ab6=4:1。已知两箱商品混合后,随机拿出一件商品是次品的概率为
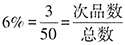
,那么商品总数应是50的整数倍,且少于100件,由此判定两箱商品总数只能是50件。乙箱商品数量为
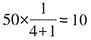
件,次品数为10×10%=1件,正品数为9件。则从乙箱中随机拿出3件商品,均不为次品的概率
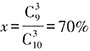
。故本题选A。
方法二,已知甲、乙两箱商品符自的次品率,以及两箱商品混合后的次品率,可运用十字交叉法,计算甲、乙两箱商品的数量比。
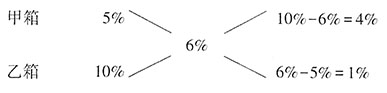
所以甲、乙两箱中商品的数量之比为4:1。根据两箱商品混合后次品率为
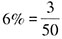
,即商品总数是50的整数倍,商品总数不到100件,可知商品总数只能是50件。乙箱商品数量为10件,次品数为1件,正品数为9件。从乙箱中随机拿出3件商品,均不为次品的概率
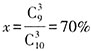
。故本题选A。
5. 某种圆珠笔单支购买1.7元/支,另有5元/3支和15元/10支两种包装供购买。办公室购买这种圆珠笔x支,最低可能的购买总价为(1.7x-2.3)元。则x可能的最大值为:______
A B C D
A
[解析] 比较三种包装的圆珠笔价格,
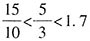
。若想总价最低,应尽可能购买15元/10支包装的笔,再购买5元/3支包装的笔。
方法一,已知办公室购买这种圆珠笔x支,最低可能的购买总价为(1.7x-2.3)元,可逐项代入验证。
A项,当x=19时,可购买1包10支和3包3支,总价为15+5×3=30元。1.7x-2.3=1.7×19-2.3=30元。A项符合。
B项,当x=21时,可购买2包10支和1支,总价为15×2+1.7=31.7元。1.7x-2.3=1.7×21-2.3=33.4元≠31.7元。B项不符合。
C项,当x=29时,可购买2包10支和3包3支,总价为15×2+5×3=45元。1.7x-2.3=1.7×29-2.3=47元≠45元。C项不符合。
D项,当x=31时,可购买3包10支和1支,总价为15×3+1.7=46.7元。1.7x-2.3=1.7×31-2.3=50.4元≠46.7元。D项不符合。故本题选A。
方法二,假设办公室购买的圆珠笔均为1.7元/支,则购买总价为1.7x元。实际购买总价为(1.7x-2.3)元,说明购买5元/3支和15元/10支包装的笔比购买单支笔优惠了2.3元。购买15元/10支包装的笔比购买单支笔优惠1.7×10-15=2元,购买5元/3支包装的笔比购买单支笔优惠1.7×3-5=0.1元。2.3=1×2+3×0.1,所以可购买1包10支和3包3支的,共1×10+3×3=19支。故本题选A。
8. 某单位举办乒乓球比赛,经过初赛之后最终只有甲、乙、丙、丁四人进入半决赛。半决赛随机抽签决定对手,胜者进入决赛。按平时的练习情况,甲对乙的胜率是
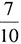
,甲对丙的胜率是

,甲对丁的胜率是
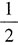
,乙对丙的胜率是
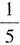
,乙对丁的胜率是
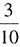
,丙对丁的胜率是

。则下列判断正确的是:______
- A.一定存在一种分组方式,丁比丙夺冠的概率更大
- B.一定存在一种分组方式,乙夺冠的概率能超过10%
- C.当甲和丁、乙和丙进行半决赛时,甲夺冠的可能性最大
- D.甲和乙进行半决赛时,甲夺冠可能性大于甲和丙进行半决赛的情况
A B C D
D
[解析] 丙对甲的胜率为
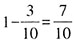
,丙对乙的胜率为
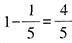
,丙对丁的胜率
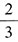
,丙对甲、乙、丁的胜率都超过

,则无论如何分组,丙夺冠的概率最大,排除A、C。
B项,半决赛乙可以与其余三人中的任意一个比赛,分三种情况讨论。乙先和甲进行半决赛,再和丙、丁之间的胜者进行决赛,乙夺冠的概率为
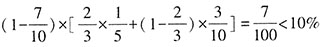
;乙先和丙进行半决赛,再和甲、丁之间的胜者进行决赛,乙夺冠的概率为
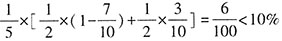
;乙先和丁进行半决赛,再和甲、丙之间的胜者进行决赛,乙夺冠的概率
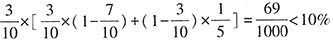
。无论哪种分组,乙夺冠的概率都低于10%,排除B。故本题选D。
验证D项,甲和乙进行半决赛,再和丙、丁之间的胜者进行决赛,甲夺冠的概率为
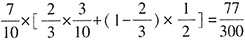
;甲和丙进行半决赛,再和乙、丁之间的胜者进行决赛,甲夺冠的概率为
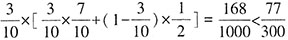
,正确。
9. 一个质量为x千克的圆台形容器如图所示,其口部半径是底面半径的2倍,在容器中装满水,总质量为9千克。从中倒出部分水使得液面高度为装满时的一半,总质量下降到4.5千克。问:x的值在以下哪个范围内?______
- A.x<1.5
- B.1.5≤x<2
- C.2≤x<2.5
- D.x≥2.5
A B C D
C
[解析] 方法一,根据圆台的上、下底面及倒出水后的液面可画图如下,DE即倒出部分水后的液面,O、N分别为上、下底面的圆心,连接ON并延长,和GC、FB的延长线交于点A,即将圆台向下延伸补全为一个圆锥。
根据题意可知,OM=MN,OG=2NC。根据△ANC∽△AME∽△AOG可知,
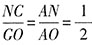
,又因MN=MO,则AN:AM:AO=1:1.5:2=2:3:4。根据相似三角形的性质可知,NC:ME:OG=2:3:4。设NC、ME、OG分别为2、3、4,设AN、AM、AO分别为2a、3a、4a。则倒出水的体积为
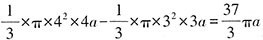
,对应的质量是9-4.5=4.5千克。剩余水的体积
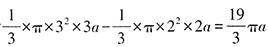
,对应的质量是(4.5-x)千克。因水的密度一定,则质量比等于体积比,可列方方程
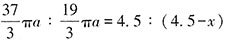
,解得x≈2.2。故本题选C。
方法二,如下图所示,ME即倒出部分水后的液面,O、N分别为上、下底面的圆心,连接ON并延长和GC的延长线交于点A。由题意可知,OM=MN,OG=2NC。根据相似三角形的性质,AN:AM:AO=NC:ME:OG=2:3:4。设NC、ME、OC,分别为2、3、4,设OM、NM、ON分别为a、a、2a。
根据圆台的体积公式
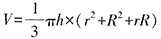
(r为上底面半径,R为下底面半径)可知,从容器中倒出的水的体积为
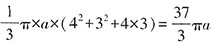
,对应的质量是9-4.5=4.5千克。容器中剩余的水的体积为
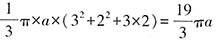
,对应的质量是(4.5-x)千克。
因水的密度一定,那么容器中剩余水的质量为
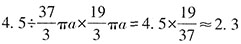
千克,则容器的质量x约为4.5-2.3=2.2千克。故本题选C。
二、定义判断每道题先给出定义,然后列出四种情况,要求你严格依据定义,从中选出一个最符合或最不符合该定义的答案。注意:假设这个定义是正确的、不容置疑的。 三、类比推理每道题先给出一组相关的词,要求你在备选答案中找出一组与之在逻辑关系上最为贴近、相似或匹配的词。 四、逻辑判断每道题给出一段陈述,这段陈述被假设是正确的、不容置疑的,要求你根据这段陈述,选择一个答案。注意:正确的答案应与所给的陈述相符合,不需要任何附加说明即可从陈述中直接推出。9. 张先生拟购买几种鲜花,购买意向如下:
(1)玫瑰、郁金香至多购买一种。
(2)牡丹、玫瑰和雏菊至少购买一种。
(3)郁金香、雏菊、百合至少购买两种。
(4)如果购买郁金香,则不购买牡丹。
根据上述意向,可以得出张先生:______
- A.必须购买百合
- B.郁金香、牡丹至少购买了一种
- C.雏菊、玫瑰至少购买了一种
- D.至少购买了三种鲜花
A B C D
C
[解析] 题干条件可整理为:①玫瑰、郁金香至多购买一种;②牡丹、玫瑰和雏菊至少购买一种;③郁金香、雏菊、百合至少购买两种;④购买郁金香→不购买牡丹。
题干有三个条件都出现了郁金香,可以对郁金香的购买情况进行假设。
假设购买郁金香,根据④可知,不购买牡丹,根据①可知,不购买玫瑰。由于不购买玫瑰、牡丹,根据②可知,购买雏菊。根据现有条件无法推知是否购买百合。
假设不购买郁金香,根据③可知,购买雏菊、百合。根据现有条件无法推知玫瑰、牡丹的购买情况。
A项,根据上述分析可知,当购买郁金香时,可以不购买百合,无法得出。
B项,根据上述分析可知,当仅购买雏菊和百合时,符合题干条件,而牡丹和郁金香可以均不购买,无法得出。
C项,根据上述分析可知,一定购买雏菊,因此“雏菊、玫瑰至少购买了一种”必然正确,可以得出。
D项,根据上述分析可知,可以仅购买郁金香、雏菊,也可以仅购买雏菊、百合,并非至少购买三种鲜花,无法得出。
故本题选C。




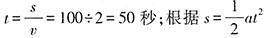 ,可知乙行驶到终点所用时间
,可知乙行驶到终点所用时间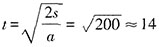 秒,乙比甲先到达终点,故该运动过程可分为三个阶段,即两车相遇前、相遇后和乙到达终点后。
秒,乙比甲先到达终点,故该运动过程可分为三个阶段,即两车相遇前、相遇后和乙到达终点后。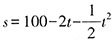 ,是开口朝下的抛物线;②甲、乙两车相遇之后,背向而行,两车之间的距离等于两车的行驶路程之和减去轨道长,那么
,是开口朝下的抛物线;②甲、乙两车相遇之后,背向而行,两车之间的距离等于两车的行驶路程之和减去轨道长,那么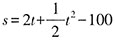 ,是开口朝上的抛物线;③乙车到达终点后,甲车继续行驶,此时两车之间的距离即甲车的行驶路程,那么s=2t,是一元一次函数。故本题选D。
,是开口朝上的抛物线;③乙车到达终点后,甲车继续行驶,此时两车之间的距离即甲车的行驶路程,那么s=2t,是一元一次函数。故本题选D。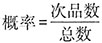 。设甲、乙两箱商品的数量分别为a、b,可列方程5%a+10%b=6%×(a+b),化简得到ab6=4:1。已知两箱商品混合后,随机拿出一件商品是次品的概率为
。设甲、乙两箱商品的数量分别为a、b,可列方程5%a+10%b=6%×(a+b),化简得到ab6=4:1。已知两箱商品混合后,随机拿出一件商品是次品的概率为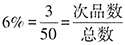 ,那么商品总数应是50的整数倍,且少于100件,由此判定两箱商品总数只能是50件。乙箱商品数量为
,那么商品总数应是50的整数倍,且少于100件,由此判定两箱商品总数只能是50件。乙箱商品数量为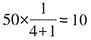 件,次品数为10×10%=1件,正品数为9件。则从乙箱中随机拿出3件商品,均不为次品的概率
件,次品数为10×10%=1件,正品数为9件。则从乙箱中随机拿出3件商品,均不为次品的概率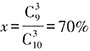 。故本题选A。
。故本题选A。
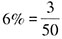 ,即商品总数是50的整数倍,商品总数不到100件,可知商品总数只能是50件。乙箱商品数量为10件,次品数为1件,正品数为9件。从乙箱中随机拿出3件商品,均不为次品的概率
,即商品总数是50的整数倍,商品总数不到100件,可知商品总数只能是50件。乙箱商品数量为10件,次品数为1件,正品数为9件。从乙箱中随机拿出3件商品,均不为次品的概率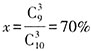 。故本题选A。
。故本题选A。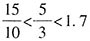 。若想总价最低,应尽可能购买15元/10支包装的笔,再购买5元/3支包装的笔。
。若想总价最低,应尽可能购买15元/10支包装的笔,再购买5元/3支包装的笔。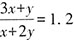 ,解得
,解得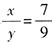 。乙企业的出资额增加50%,即1.5x,则其分配的利润为甲企业的
。乙企业的出资额增加50%,即1.5x,则其分配的利润为甲企业的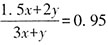 。故本题选B。
。故本题选B。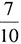 ,甲对丙的胜率是
,甲对丙的胜率是 ,甲对丁的胜率是
,甲对丁的胜率是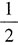 ,乙对丙的胜率是
,乙对丙的胜率是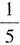 ,乙对丁的胜率是
,乙对丁的胜率是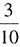 ,丙对丁的胜率是
,丙对丁的胜率是 。则下列判断正确的是:______
。则下列判断正确的是:______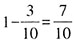 ,丙对乙的胜率为
,丙对乙的胜率为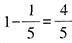 ,丙对丁的胜率
,丙对丁的胜率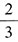 ,丙对甲、乙、丁的胜率都超过
,丙对甲、乙、丁的胜率都超过 ,则无论如何分组,丙夺冠的概率最大,排除A、C。
,则无论如何分组,丙夺冠的概率最大,排除A、C。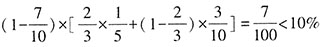 ;乙先和丙进行半决赛,再和甲、丁之间的胜者进行决赛,乙夺冠的概率为
;乙先和丙进行半决赛,再和甲、丁之间的胜者进行决赛,乙夺冠的概率为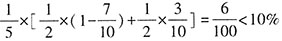 ;乙先和丁进行半决赛,再和甲、丙之间的胜者进行决赛,乙夺冠的概率
;乙先和丁进行半决赛,再和甲、丙之间的胜者进行决赛,乙夺冠的概率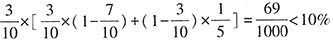 。无论哪种分组,乙夺冠的概率都低于10%,排除B。故本题选D。
。无论哪种分组,乙夺冠的概率都低于10%,排除B。故本题选D。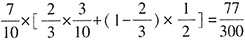 ;甲和丙进行半决赛,再和乙、丁之间的胜者进行决赛,甲夺冠的概率为
;甲和丙进行半决赛,再和乙、丁之间的胜者进行决赛,甲夺冠的概率为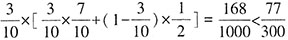 ,正确。
,正确。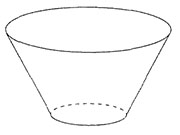
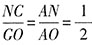 ,又因MN=MO,则AN:AM:AO=1:1.5:2=2:3:4。根据相似三角形的性质可知,NC:ME:OG=2:3:4。设NC、ME、OG分别为2、3、4,设AN、AM、AO分别为2a、3a、4a。则倒出水的体积为
,又因MN=MO,则AN:AM:AO=1:1.5:2=2:3:4。根据相似三角形的性质可知,NC:ME:OG=2:3:4。设NC、ME、OG分别为2、3、4,设AN、AM、AO分别为2a、3a、4a。则倒出水的体积为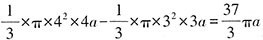 ,对应的质量是9-4.5=4.5千克。剩余水的体积
,对应的质量是9-4.5=4.5千克。剩余水的体积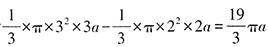 ,对应的质量是(4.5-x)千克。因水的密度一定,则质量比等于体积比,可列方方程
,对应的质量是(4.5-x)千克。因水的密度一定,则质量比等于体积比,可列方方程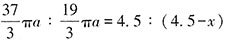 ,解得x≈2.2。故本题选C。
,解得x≈2.2。故本题选C。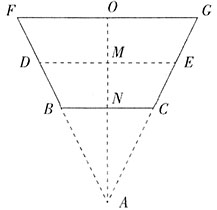
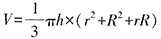 (r为上底面半径,R为下底面半径)可知,从容器中倒出的水的体积为
(r为上底面半径,R为下底面半径)可知,从容器中倒出的水的体积为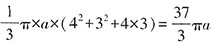 ,对应的质量是9-4.5=4.5千克。容器中剩余的水的体积为
,对应的质量是9-4.5=4.5千克。容器中剩余的水的体积为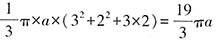 ,对应的质量是(4.5-x)千克。
,对应的质量是(4.5-x)千克。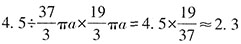 千克,则容器的质量x约为4.5-2.3=2.2千克。故本题选C。
千克,则容器的质量x约为4.5-2.3=2.2千克。故本题选C。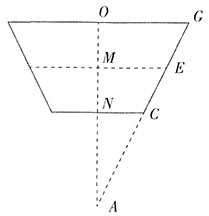
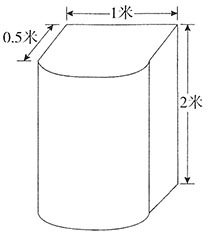
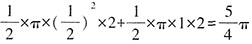 平方米。那么平均每平方米的涂漆成本为
平方米。那么平均每平方米的涂漆成本为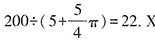 元。故本题选B。
元。故本题选B。

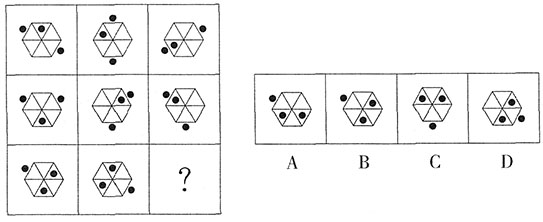

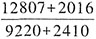 。
。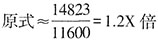 ,最接近的是B。
,最接近的是B。 。
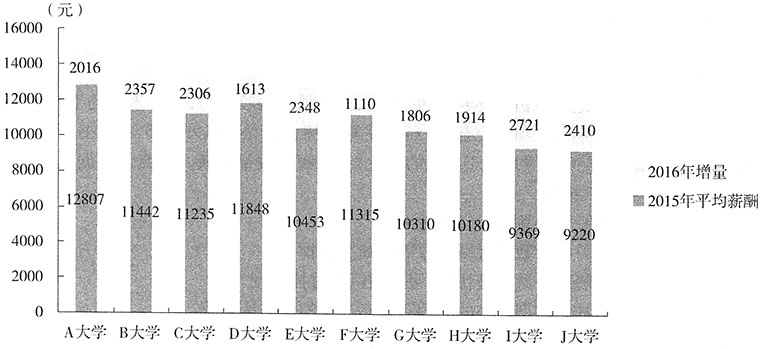
。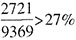 ,简单估算其他大学的增速,除了J大学,其余大学的增速均未超过25%,J大学的增速为
,简单估算其他大学的增速,除了J大学,其余大学的增速均未超过25%,J大学的增速为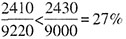 ,所以I大学的增逐最快,能够推出。
,所以I大学的增逐最快,能够推出。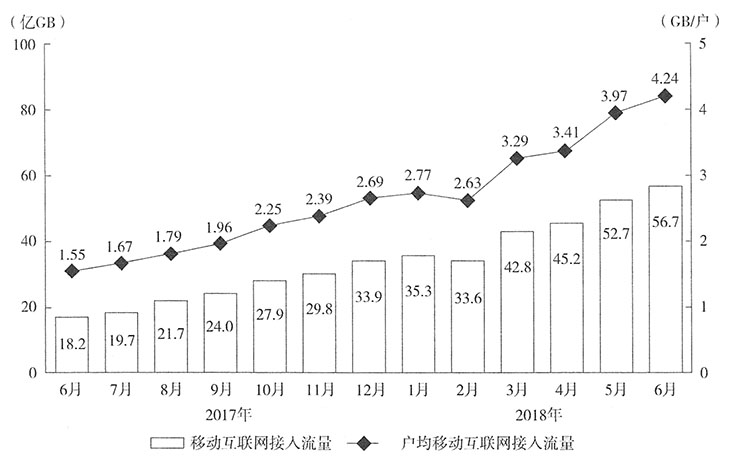
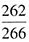 ,通过非手机设备上网的占比为
,通过非手机设备上网的占比为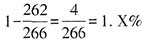 ,故本题选B。
,故本题选B。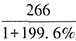 亿GB。根据条形图可知,2017年下半年全国移动互联网接入流量为19.7+21.7+24.0+27.9+29.8+33.9=157亿GB,则所求为
亿GB。根据条形图可知,2017年下半年全国移动互联网接入流量为19.7+21.7+24.0+27.9+29.8+33.9=157亿GB,则所求为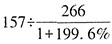 。
。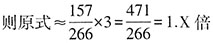 。符合题意的只有A。
。符合题意的只有A。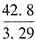 亿户。
亿户。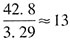 ,即所求约为13亿户。
,即所求约为13亿户。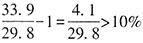 ,即环比增速超过10%,可以推出。
,即环比增速超过10%,可以推出。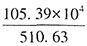 。
。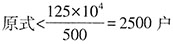 ,不到3000户。故本题选A。
,不到3000户。故本题选A。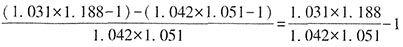 。
。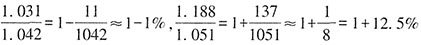 ,则原式≈(1-1%)×(1+12.5%)-1≈11.5%,增长了5%以上。故本题选B。
,则原式≈(1-1%)×(1+12.5%)-1≈11.5%,增长了5%以上。故本题选B。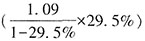 亿元。由前面题目可知,企业户数为
亿元。由前面题目可知,企业户数为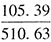 万户,则所求为
万户,则所求为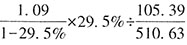 。
。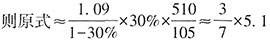 ,列式结果的首位数为2,单位为万元。
,列式结果的首位数为2,单位为万元。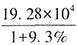 万元;2017年人均年薪酬6.64万元,比2016年增加0.60万元,故2016年人均年薪酬为6.64-0.60=6.04万元,所求为
万元;2017年人均年薪酬6.64万元,比2016年增加0.60万元,故2016年人均年薪酬为6.64-0.60=6.04万元,所求为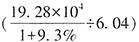 人。
人。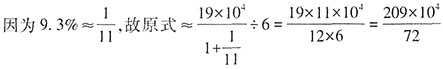 ,列式结果的前两位数字为29,只有C项符合。
,列式结果的前两位数字为29,只有C项符合。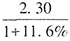 ,营业税金及附加为
,营业税金及附加为 。前者是后者的
。前者是后者的
 倍,即2016年企业缴纳营业增值税没有超过营业税金及附加的2倍,无法推出。
倍,即2016年企业缴纳营业增值税没有超过营业税金及附加的2倍,无法推出。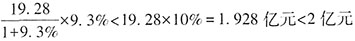 ,无法推出。
,无法推出。 ”,根据两期平均数大小比较的核心结论可知,-29.5%<3.1%,则2017年S市服务业小微样本企业平均每万元营业收入缴纳营业税及附加低于上年水平,无法推出。
”,根据两期平均数大小比较的核心结论可知,-29.5%<3.1%,则2017年S市服务业小微样本企业平均每万元营业收入缴纳营业税及附加低于上年水平,无法推出。