一、1. 工程上,梁的斜弯曲可以分解为______;梁发生偏心压缩[拉伸]时,变形可分解为______的变形组合。
以两个主轴为中性轴发生的两个平面弯曲,压缩[拉伸]与弯曲。
2. 长为dx的圆轴微段受扭转作用的变形能表达式为______,表达式中各符号的物理(几何) 意义为______。
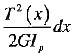
,T(x) 是扭矩,G是剪切弹性模量,I
P是极惯矩。
3. 材料力学主要研究构件在______范围内的______变形情况。因构件是变形固体,在研究构件的平衡时,应按变形______的尺寸进行计算。
二、1. 压杆稳定设计的内容一般包括那几个方面?
压杆稳定设计中需要考虑四方面的影响:压杆长度,约束条件,压杆的细长比及材料的影响。
2. 具有对称面的梁受外力作用时,什么情况下发生斜弯曲?
在横向力通过弯曲中心,但不与形心主轴平行的情况下,梁将发生斜弯曲。
3. 由下图所示三角形薄板,a=120mm,受外力作用而变形,角点B垂直向上位移为δ=0.03mm,但AB和BC仍保持为直线,试求OB的平均应变和AB与BC两边在B点的角度改变。
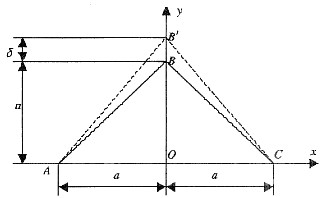
由应变定义
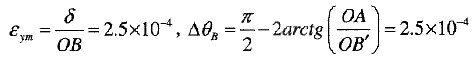
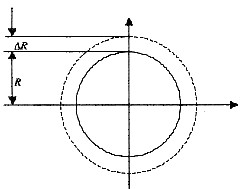
4. 求下图所示圆形薄板在半径方向和外圆周方向的平均线应变。已知外圆半径R=80mm,半径增加量△R=3×10
-3mm。
三、1. 图示为一组合轴,由变截面空心铜轴和实心钢轴组成,两轴间无相对滑动。铜和钢的剪切弹性模量分别为G
C和G
S。试求组合轴承受扭矩T时的切应力公式。
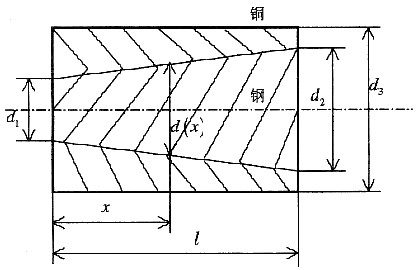
钢轴直径
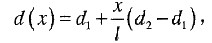
钢轴的极惯性矩
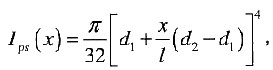
铜轴的极惯性矩
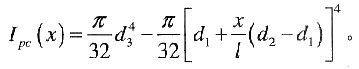
因为两轴间无相对滑动,所以两轴的单位长度扭转角相等,即变形几何条件成立:θ
s=θ
c。
两轴在同一截面处的扭矩是T
c(x) +T
s(x) =T。而物理条件:
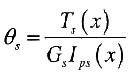
,
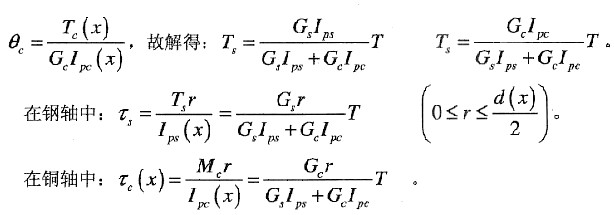
2. 如图所示-U形刚架ABCD,三段长度均为L,且抗弯刚度均为EI,现要保证在F
1和F
2作用下A与D间无相对位移(不考虑轴力和剪力的作用) ,应如何匹配F
1和F
2的大小?
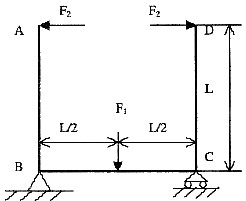
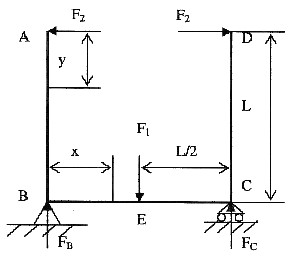
由于对称,所以支反力
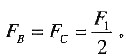
AB杆的弯矩方程:
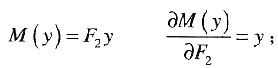
BE杆的弯矩方程:
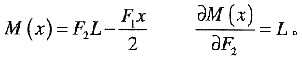
A,D两点的相对位移为
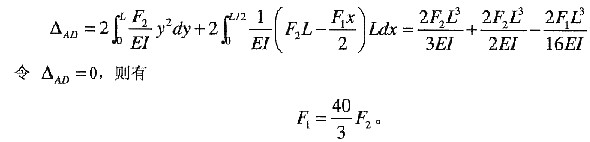
3. 求下图所示矩形截面梁AB承受的最大应力。梁截面的宽为b,高为h。
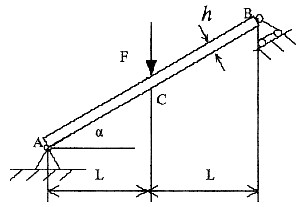

AB梁发生压弯组合变形,E
x=F sinα,F
v=F cosα。压应力σ
N=F sinα/A。
最大弯矩
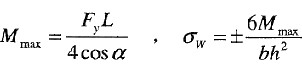
。
最大拉应力发生在点C右截面下边缘

。
最大压应力发生在点C左截面上边缘
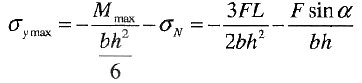
。
4. 如图所示,有一截面为矩形的闭口薄壁杆件,其截面面积A和厚度δ之积保持不变,而比值β=a/b可以改变。试证明:在扭矩T作用下,切应力τ正比于(1+β)
2/β。
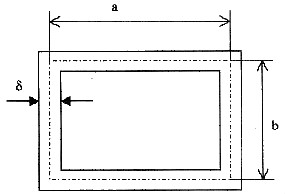
证明:由2(a+b) δ=const,所以2b(a/b+1) δ=const,得
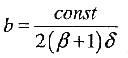
。
截面上的应力为:
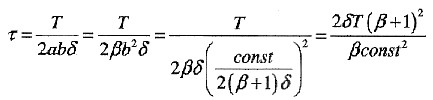
所以
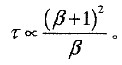
5. 已知应力状态如图所示。(1) 求出主应力大小和主平面位置;(2) 求出此应力状态下的应力圆的圆心和半径。
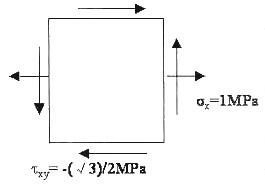
已知条件
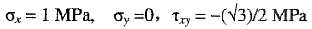
,求主应力
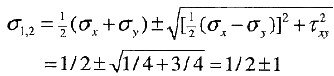
即σ
1=3/2,σ
2=-1/2。
应力圆心坐标为(σ
1十σ
2) /2=1/2;应力圆半径为(σ
1-σ
2) /2=1;
主平面位置
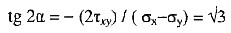
。
6. 一变截面的外伸梁如图所示,AB段的刚度为EI
1,BC段的刚度为EI
2,在C端受集中力F的作用,求截面C的挠度和转角。
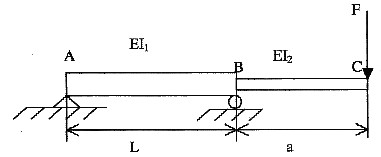
先设梁在B点的截面不转动,BC段视为悬臂梁,如图所示。由转角和挠度公式可得
θ
c1=F·a
2/(2EI
2) ,y
c1=-F·a
3/(3EI
2) 。
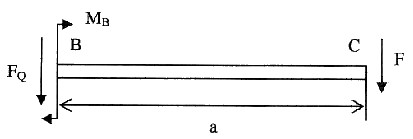
以B点右端处将梁截开,列平衡方程,F
Q+F=0;F
Q=-F;
∑M
B=0,-MB-F·a=0,解得M
B=-F·a。其中剪力FQ可由B端的支座反力所平衡,不引起梁的变形,而弯矩M
B相当于一集中力偶,在B端产生的转角为
θ
c2=θ
B=-F·a·L(3EI
1) ,y
c2=θB·a=-F·a
2·L/(3EI
1) ,
所以θ=θ
c1+θ
c2=-F·a
2/(2EI
2) -F·a·L/(3EI
1) ,y
c=y
c1+y
c2=-F·a
3/(3EI
2) -F·a
2·L/(3EI
1) 。