银符考试题库B12
现在是：
试卷总分：150.0
您的得分：
考试时间为：
点击“开始答卷”进行答题
交卷
评分
存入我的题库
晒成绩
打印模式
隐藏答案解析
打印
下载
背景
字体
较大
大
中
小
较小
退出
流体力学B卷真题2007年
一、
提示：张量形式的动量方程为
1. 在描述流动时常用到流线、迹线和脉线等概念。试问陨星下坠时在天空划过的白线是什么线?烟囱里冒出的烟是什么线?
陨星下坠时在天空划过的白线是迹线，烟囱里冒出的烟是脉线(或烟线) 。
2. 流动满足质量守恒的数学表达式是什么?对于不可压缩流动，它被简化成什么?
，对于不可压缩流动，简化为
。
3. 试述物质导数(又称随体导数) 和当地导数的定义，并阐明两者关系。
物质导数是研究流体随体运动的物理量的时间变化率，数学描述为
；当地导数是指欧拉描述中空间点上的物理量随时间的变化率，数学描述为
。两者间的关系为
。
4. 作用于流体微元的力分为体积力和面积力两类。体积力做功会改变流体的内能吗?流体的内能改变通常由哪些因素决定?
体积力不会改变流体的内能。改变内能的因素有体积应变率(可压缩性) 、粘性力做功、热传导、辐射和化学反应等。
5. 要研究在大气中飞行的真实飞机受力情况，通常会在实验室里通过测量飞机模型在风洞中的受力来进行比拟。请问，要使该实验具有说服力，必须满足哪些相似条件?
要使得实验具有说服力，必须满足几何相似、时间相似、运动相似和动力相似。流动控制参数相等，即St、Re等，边界条件相似，即要求无量纲后的物理量边界条件相等。
二、
1. 已知速度分布a=x
2
-y
2
，v=-2xy，w=0。求流线方程。
该流动满足无旋条件
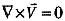
，则存在流函数ψ，满足
．
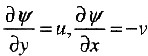
积分得到
。
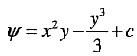
该问题中流线就是流函数的等值线，所以流线方程是
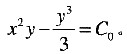
2. 以Lagrange变量(a，b，c) 给出的流场
x=ae
-2t/k
，y=b(1+t/k)
2
，z=ce
t/k
(1+t/k)
-2
式中k为非零常数。请判断该流场(a) 是否定常?
(b) 是否是可压缩的?
(c) 是否是有旋流场?
根据Lagrange描述得
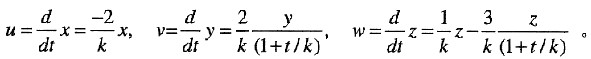
(a) 因为速度u，v，w是时间的函数，因此该流动为非定常流动。
(b)
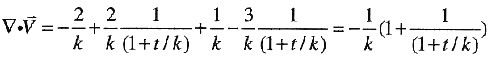
，所以流动可压缩。
(c)
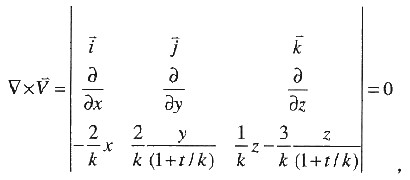
所以流动是无旋的。
3. 如图，两无穷大平行平板的间距为h，中间充满着不可压缩粘性流体，上板(z=h) 相对于下板(z=0) 在自身平面内以不变的速度u=U沿x轴运动，同时流场受到沿x轴的常压力梯度
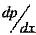
=-G的作用。若流体的粘性系数为μ，求流动达到定常时的速度场和体积流量。
满足该流动的动量方程为
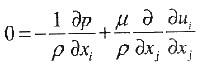
简化得0=
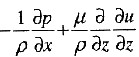
，边界条件为：y=0，u=0；y=h，u=U。
解得
。
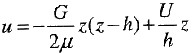
则体积流量为
。
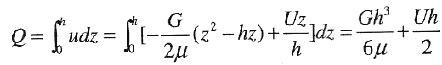
一、
1
2
3
4
5
二、
1
2
3
深色：已答题 浅色：未答题
提交纠错信息
评价难易度
提交知识点
，对于不可压缩流动，简化为
。
；当地导数是指欧拉描述中空间点上的物理量随时间的变化率，数学描述为
。两者间的关系为
。
，则存在流函数ψ，满足
．
。
，所以流动可压缩。
=-G的作用。若流体的粘性系数为μ，求流动达到定常时的速度场和体积流量。
，边界条件为：y=0，u=0；y=h，u=U。
。
。
深色：已答题 浅色：未答题