数量关系8. 同样价格的某商品在4个商场销售时都进行了两次价格调整。甲商场第一次提价的百分率为a,第二次提价的百分率为b(a>0,b>0,且a≠b);乙商场两次提价的百分率均为

;丙商场第一次提价的百分率为

,第二次提价的百分率为

;丁商场第一次提价的百分率为b,第二次提价的百分率为a。那么,两次提价后该商品售价最高的商场是______。
A B C D
B
[解析] 设该商品原来的价格为1,则4个商场经过两次价格调整后的售价如下:
甲商场:(1+a)×(1+b))=1+a+b+ab;
乙商场:

丙商场:

丁商场:(1+b)×(1+a)=1+a+b+ab。
易知甲、丁两商场两次提价后售价相同,不可能是最高的,故排除A、D两项。比较乙、丙两商场两次提价后的售价,只需比较

的大小即可,明显有

,即乙商场该商品两次提价后的售价最高。故本题选B。
9. 6对新人举办集体婚礼,6位新娘分别坐入6顶花轿中,每位新郎任选一顶花轿且每顶花轿均有人选择,则恰好只有1位新郎选对自己新娘的概率为:______
A.

B.

C.

D.
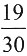
A B C D
B
[解析] 本题为概率问题,给情况数求概率,则概率=

。总情况数为6位新郎选择6顶花轿,共有

=6!种情况。满足情况数为恰好只有1位新郎选对自己新娘,即6位新郎中有1位选对,其余5位均选错,6位新郎任选1位,有

种情况,其他5位新郎没选对新娘,即5人错位排列,有D
5=44种情况,所以共有

×D
5=(6×44)种情况。财概率=
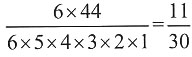
。
故正确答案为B。
12. 如图,有两个小正方形和一个大正方形,大正方形的边长是小正方形边长的2倍,阴影部分三角形面积为240,请问三个正方形的面积和是多少?______
A B C D
C
[解析] 设小正方形边长为x,连接大正方形的对角线,得到阴影三角形的底边为
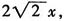
高为
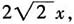
则
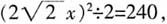
x
2=60。三个正方形的面积和为2x
2+(2x)
2=6x
2=360。本题也可如下考虑,大正方形面积是小正方形面积的4倍,则三个正方形面积之和应是6的倍数,选项中只有C是6的倍数,故选择C。
13. 一个袋子里面有10个球,包括红球、白球和黑球。已知从袋中任意摸一个球,得到黑球的概率是

从袋中任意摸两个球,至少有一个是白球的概率是

问袋子里有多少个红球?______
A B C D
A
[解析] 任意摸一个球,得到黑球的概率是
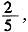
因此黑球有
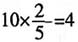
个。设白球有x个,那么任意摸两个球,至少有一个是白球的概率为

解得x=5,故红球有10-4-5=1个。
15. 连接正方体每个面的中心构成一个正八面体(如下图所示)。已知正方体的边长为6厘米,则正八面体的体积为______立方厘米。
A.
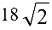
B.
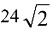
C.36
D.72
A B C D
C
[解析] 由图中可以看出,将正八面体拆解为两个完全相同的四棱锥,而每个棱锥的体积

,高度h正好为正方体边长的一半,即3厘米,现在只需要求棱锥的底面积S。将棱锥的底面单独拿出来看,如下图所示:
棱锥底面积正好等于正方体底面积的一半,即为6×6÷2=18平方厘米。因此每个棱锥的体积为

立方厘米,正八面体体积为18×2=36立方厘米。
17. 在政策的扶持下,老李决定在自家29亩稻田中养蟹,每亩稻田可养殖180千克的蟹。到了蟹上市的时节,老李捕捞蟹的量从第二天起,每天都比前一天多20千克,直到第18天刚好捕捞完。捕捞的蟹当天售卖,前一半时间蟹的销售价格是后一半时间的1.5倍,最终老李销售蟹的总收入为61.2万元,则前一半时间蟹的销售价格是多少?______
- A.100元/千克
- B.125元/千克
- C.150元/千克
- D.200元/千克
A B C D
C
[解析] 已知老李捕捞蟹的总量为(29×180)千克,每天捕捞蟹的量是公差为20(千克)、项数为18的等差数列,设第一天捕捞蟹的量为a
1千克,根据等差数列求和公式“
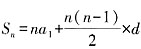
”可知,
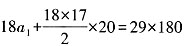
,解得a
1=120。根据等差数列中项求和公式可知,前9天捕捞蟹的量为9×(120+4×20)=1800千克,则后9天捕捞蟹的量为29×180-1800=3420千克。设后9天蟹的销售价格为x元/千克,则前9天蟹的销售价格为1.5x元/千克,可列方程1800×1.5x+3420×x=61.2×10
4,解得x=100,则前一半时间蟹的销售价格为1.5x=150元/千克。故本题选C。
18. 某办公用品店举办促销活动,打八五折出售某款耗材,活动第一天销量是未打折时的3倍,利润是未打折时的1.2倍。活动第二天打九折出售,则销量要是未打折时的多少倍,两天活动的平均利润才能与平时相当?______
A.

B.1.5
C.
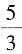
D.2
A B C D
A
[解析] 根据题意,假设耗材成本价为x,促销前售价为100,每天销量为1,则利润为(100-x)。活动第一天售价为85,销量为3,利润为(85-x)×3=1.2(100-x),解得x=75,则活动第一天利润为(85-75)×3=30。活动第二天售价为90,两天活动的平均利润要想与平时相当,活动第二天的利润应该达到(100-75)×2-30=20,销量应为未打折时的20÷(90-75)=
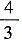
倍。故本题选A。
19. 如图,已知三角形ABC的面积为8cm
2,AE=ED,

则阴影部分的面积为______。
A B C D
C
[解析] 几何问题。如图所示,连接DF,因为AE=ED,所以S△DFE=S△AEF,S△ABE=S△BED;因为

所以BD=2DC,S△BDF=2S△FDC(同高底共线,面积比=底长比)。设△AFE=S
1,△FDC=S
2,则S△ABE=S△BED=2S-S。因为S△ABC=8cm
2,所以8=2(2S
2-S
1)+2S
1+S
2=5S
2,
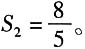
阴影部分的面积为:

故选C。
28. 某年级有甲、乙、丙、丁四个兴趣小组,甲和丁小组人数之和是乙和丙人数之和的2倍,甲小组人数是乙的5倍,丙小组人数是丁的3倍。问:丁小组人数相当于四个小组总人数的:______
A.
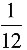
B.
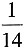
C.

D.
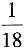
A B C D
B
[解析] 根据题意有,甲+丁=2(乙+丙)①,甲=5乙②,丙=3丁③,将②③代入①中,可得3乙=

丙,总人数=3(乙+丙)=

丙=14丁,则丁小组人数相当于四个小组总人数的

。故本题选B。
35. 一项工作,若甲单独做可比规定时间提前3天完成,若乙单独做则要比规定时间多5天才能完成。现甲、乙两人合作了4天,剩下的由乙单独做,结果正好按时完成。甲、乙两人合作需______天即可完成这项工作。
A B C D
B
[解析] 由“乙单独做需要比规定时间多5天才能完成”和“甲、乙两人合作了4天,剩下的由乙单独做,结果正好按时完成”可知,甲做4天相当于乙做5天所完成的工作量。因此甲的效率是乙的效率的

倍。两人单独做,乙所需要的时间比甲多8天。
方法一:甲完成这项工作所需要的时间=8÷(

-1)=32(天)。所以甲、乙两人合作完成这项工作所需要的时间=32÷(1+

)=

。
方法二:设工作量为1,甲的速度为5a,乙的速度为4a,则有

,得a=

。那么,题目所求为

。故答案为B。
45. 某市公租房的房源位于A、B、C三个片区,若每位符合条件的申请者只能申请其中一个片区的房源,且申请任何一个片区的房源都是等可能的,那么该市任意4名申请者中有人与其他人不存在竞争关系的概率是:______
A.

B.

C.

D.

A B C D
B
[解析] “不存在竞争关系”即4人中有人申请的片区与其他三人不重叠。申请公租房的情况有3
4=81种;3人申请在同一片区情况有

种;2人申请在同一片区,其他片区各1人的情况有

种;则任意4名申请者中有人与其他人不存在竞争关系的概率是

。故本题选B。
 。故本题选C。
。故本题选C。

 ;丙商场第一次提价的百分率为
;丙商场第一次提价的百分率为 ,第二次提价的百分率为
,第二次提价的百分率为 ;丁商场第一次提价的百分率为b,第二次提价的百分率为a。那么,两次提价后该商品售价最高的商场是______。
;丁商场第一次提价的百分率为b,第二次提价的百分率为a。那么,两次提价后该商品售价最高的商场是______。

 的大小即可,明显有
的大小即可,明显有 ,即乙商场该商品两次提价后的售价最高。故本题选B。
,即乙商场该商品两次提价后的售价最高。故本题选B。


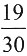
 。总情况数为6位新郎选择6顶花轿,共有
。总情况数为6位新郎选择6顶花轿,共有 =6!种情况。满足情况数为恰好只有1位新郎选对自己新娘,即6位新郎中有1位选对,其余5位均选错,6位新郎任选1位,有
=6!种情况。满足情况数为恰好只有1位新郎选对自己新娘,即6位新郎中有1位选对,其余5位均选错,6位新郎任选1位,有 种情况,其他5位新郎没选对新娘,即5人错位排列,有D5=44种情况,所以共有
种情况,其他5位新郎没选对新娘,即5人错位排列,有D5=44种情况,所以共有 ×D5=(6×44)种情况。财概率=
×D5=(6×44)种情况。财概率=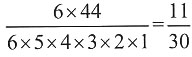 。
。

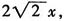 高为
高为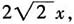 则
则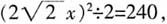 x2=60。三个正方形的面积和为2x2+(2x)2=6x2=360。本题也可如下考虑,大正方形面积是小正方形面积的4倍,则三个正方形面积之和应是6的倍数,选项中只有C是6的倍数,故选择C。
x2=60。三个正方形的面积和为2x2+(2x)2=6x2=360。本题也可如下考虑,大正方形面积是小正方形面积的4倍,则三个正方形面积之和应是6的倍数,选项中只有C是6的倍数,故选择C。 从袋中任意摸两个球,至少有一个是白球的概率是
从袋中任意摸两个球,至少有一个是白球的概率是 问袋子里有多少个红球?______
问袋子里有多少个红球?______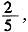 因此黑球有
因此黑球有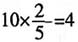 个。设白球有x个,那么任意摸两个球,至少有一个是白球的概率为
个。设白球有x个,那么任意摸两个球,至少有一个是白球的概率为 解得x=5,故红球有10-4-5=1个。
解得x=5,故红球有10-4-5=1个。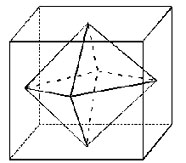
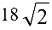
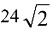
 ,高度h正好为正方体边长的一半,即3厘米,现在只需要求棱锥的底面积S。将棱锥的底面单独拿出来看,如下图所示:
,高度h正好为正方体边长的一半,即3厘米,现在只需要求棱锥的底面积S。将棱锥的底面单独拿出来看,如下图所示:
 立方厘米,正八面体体积为18×2=36立方厘米。
立方厘米,正八面体体积为18×2=36立方厘米。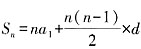 ”可知,
”可知,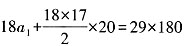 ,解得a1=120。根据等差数列中项求和公式可知,前9天捕捞蟹的量为9×(120+4×20)=1800千克,则后9天捕捞蟹的量为29×180-1800=3420千克。设后9天蟹的销售价格为x元/千克,则前9天蟹的销售价格为1.5x元/千克,可列方程1800×1.5x+3420×x=61.2×104,解得x=100,则前一半时间蟹的销售价格为1.5x=150元/千克。故本题选C。
,解得a1=120。根据等差数列中项求和公式可知,前9天捕捞蟹的量为9×(120+4×20)=1800千克,则后9天捕捞蟹的量为29×180-1800=3420千克。设后9天蟹的销售价格为x元/千克,则前9天蟹的销售价格为1.5x元/千克,可列方程1800×1.5x+3420×x=61.2×104,解得x=100,则前一半时间蟹的销售价格为1.5x=150元/千克。故本题选C。
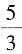
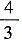 倍。故本题选A。
倍。故本题选A。 则阴影部分的面积为______。
则阴影部分的面积为______。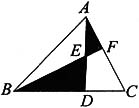
 所以BD=2DC,S△BDF=2S△FDC(同高底共线,面积比=底长比)。设△AFE=S1,△FDC=S2,则S△ABE=S△BED=2S-S。因为S△ABC=8cm2,所以8=2(2S2-S1)+2S1+S2=5S2,
所以BD=2DC,S△BDF=2S△FDC(同高底共线,面积比=底长比)。设△AFE=S1,△FDC=S2,则S△ABE=S△BED=2S-S。因为S△ABC=8cm2,所以8=2(2S2-S1)+2S1+S2=5S2,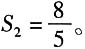 阴影部分的面积为:
阴影部分的面积为: 故选C。
故选C。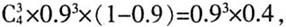 4人全被治愈的概率为0.94,因此至少3人被治愈的概率为两者之和,0.93×(0.4+0.9)=0.9477,选C。
4人全被治愈的概率为0.94,因此至少3人被治愈的概率为两者之和,0.93×(0.4+0.9)=0.9477,选C。
 ,解得x%=27.5%,因此余下的桌椅是打
,解得x%=27.5%,因此余下的桌椅是打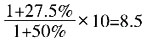 折出售的。
折出售的。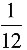
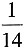

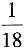
 丙,总人数=3(乙+丙)=
丙,总人数=3(乙+丙)= 丙=14丁,则丁小组人数相当于四个小组总人数的
丙=14丁,则丁小组人数相当于四个小组总人数的 。故本题选B。
。故本题选B。 解得
解得 所以食堂每天最多供125人用餐能保证食用油库存不被消耗。故本题选A。
所以食堂每天最多供125人用餐能保证食用油库存不被消耗。故本题选A。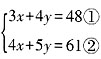 ,①×4-②×3得y=9,则2班女学生有5×9=45人。故本题选C。
,①×4-②×3得y=9,则2班女学生有5×9=45人。故本题选C。 倍。两人单独做,乙所需要的时间比甲多8天。
倍。两人单独做,乙所需要的时间比甲多8天。 -1)=32(天)。所以甲、乙两人合作完成这项工作所需要的时间=32÷(1+
-1)=32(天)。所以甲、乙两人合作完成这项工作所需要的时间=32÷(1+ )=
)= 。
。 ,得a=
,得a= 。那么,题目所求为
。那么,题目所求为 。故答案为B。
。故答案为B。 ,问这堆立方体最少有多少个?______
,问这堆立方体最少有多少个?______
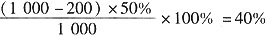 ,第二次倒出200克后,浓度变为
,第二次倒出200克后,浓度变为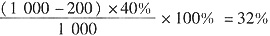 ,第三次倒出200克后,浓度变为
,第三次倒出200克后,浓度变为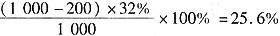 。故选C。
。故选C。
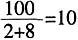 天。选C。
天。选C。



 种;2人申请在同一片区,其他片区各1人的情况有
种;2人申请在同一片区,其他片区各1人的情况有 种;则任意4名申请者中有人与其他人不存在竞争关系的概率是
种;则任意4名申请者中有人与其他人不存在竞争关系的概率是 。故本题选B。
。故本题选B。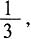 乙溶液倒掉一半,然后混合在一起,此时得到溶液浓度约为:______
乙溶液倒掉一半,然后混合在一起,此时得到溶液浓度约为:______