银符考试题库B12
现在是：
试卷总分：100.0
您的得分：
考试时间为：
点击“开始答卷”进行答题
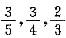装配若干机器，那么原来存有甲种部件 ．
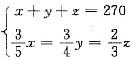，解得
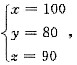选(C)．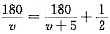
，解得v=40或v=-45(舍去)，故提速后为v=45，选(B)．
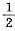(D)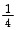 
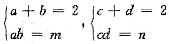，已知四个根为首项为
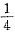的等差数列，所以末项应为
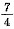，从而可得中间两项分别为
，m，n分别为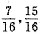
．从而等差数列为
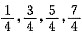所以|m-n|=
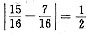．选(C)．
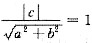，所以a2+b2=c2，选(B)．
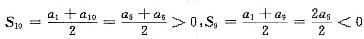，选(C)．
=
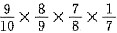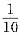，选(D)．
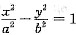，则取M的坐标为(0，b)，而F1的坐标为(c，0)，又∠OMF2=60°，即
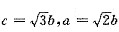，所以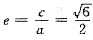
，选(B)．
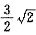，设球半径为r，则
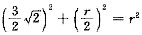，即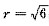
，所以球体积为
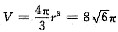，选(B)．
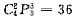，选(C)．
|z-i|=5，表示圆心在(0，1)，半径为5的圆，选(C)．
的半径为 ．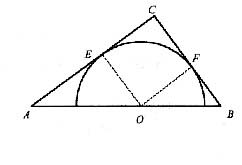
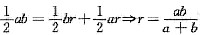，选(B)．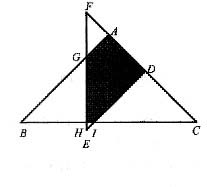
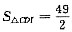；AB=12，AG=3，BG=9，故
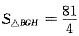，从而阴影部分面积是S△ABC-S△BGH=S△CDI=
，选(D)．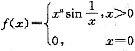
，则下列结论中错误的是 ．
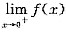不存在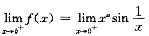
不存在，(A)正确；0＜a≤1时，
=
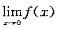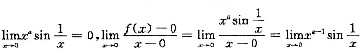不存在，故f(x)在x=0处连续但不可导，B正确；1＜a＜2时，
．
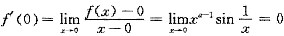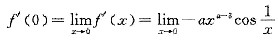不存在，故f(x)在x=0处可导但导函数不连续，(C)正确；a=2时，f'(0)=
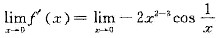不存在，(D)错误，选(D)．
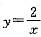在x＞0的某点处相切，则k= ．
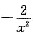，令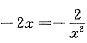
，即x=1，y=2，所以，两直线过(1，2)点，从而有k=3，选(C)．
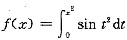，当x→0时，与f(x)等价的无穷小量是 ．
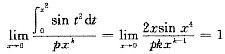，有k=6，
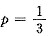，即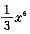
，选(D)．
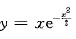与直线x=-2，x=2及x轴所围成的平面图形的面积为 ．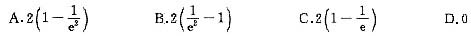
在(-2，2)内是奇函数，所以
=
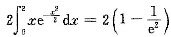，选(A)．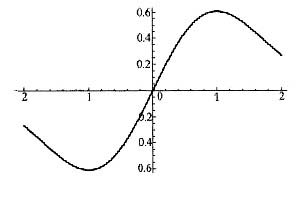
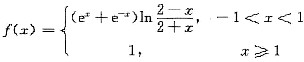，则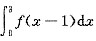
= ．
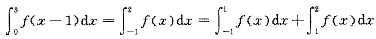，而-1＜x＜1时f(x)为奇函数，故
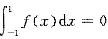，又
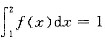，所以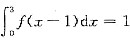
，选(C)．
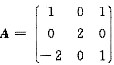，则|B|=( )．
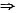(A-E)B=A+E，由A-E可逆，从而|B|=|(A-E)-1(A+E)|=9，选(B)．
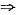2A2+8A+E=0，有(A+E)(2A+6E)=5E，故A+E可逆；(A+2E)(2A+4E)=7E，故A+2E可逆；(A+3E)(2A+2E)=5E，故A+3E可逆；2A(A+4E)=-E，故A+4E可逆，选(D)．
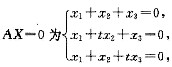若存在3阶非零矩阵B，使得AB=0，则 ．
，显然t=1时，B矩阵只要满足r(B)≤2即可，若t≠1需要B=0，选(D)．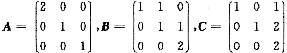
，则 ．
深色：已答题 浅色：未答题