一、单项选择题(在每小题给出的四个选项中,有一项是符合题目要求的)
二、多项选择题(以下每小题的备选答案中,有两个或两个以上选项符合题目要求)
三、填空题1. 美国行为主义心理学家______曾经说过,给他一打健康的婴儿,不管他们祖先的状况如何,他可以任意把他们培养成从领袖到小偷等各种类型的人.
2. 《义务教育数学课程标准》的总目标的四个方面是______、______、______、______.
3. “数与代数”的教学应遵循的原则是______、______、______.
一、选择题(在每小题给出的四个选项中,有一项是符合题目要求的)
1. 设集合I={(x,y)|x∈R,y∈R},A={(x,y)|2x-y+m>0},B={(x,y)|x+y-n≤0},那么点P(2,3)∈A∩(C
IB)的充要条件是
.
- A.m>-1,n<5
- B.m<-1,n<5
- C.m>-1,n>5
- D.m<-1,n>5
A B C D
A
[解析] 由题设知P(2,3)∈A,且P(2,3)∈C
IB,
又C
IB={(x,y)|x+y-n>0},∴可得
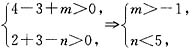
故本题应选A.
4. 给出下列三个命题:
①函数
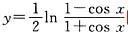
与
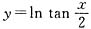
是同一函数;
②若函数y=f(x)与y=g(x)的图象关于直线y=x对称,则函数y=f(2x)与y=
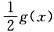
的图象也关于直线y=x对称;
③若奇函数f(x)对定义域内任意x都有f(x)=f(2-x),则f(x)为周期函数.其中真命题是
.
A B C D
C
[解析] ①函数
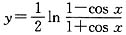
的定义域满足
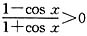
,即cosx≠±1,x≠kπ(k∈Z),
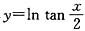
的定义域满足
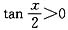
,即
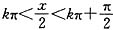
,2kπ<x<2kπ+π(k∈Z),两函数定义域不相同,不是同一函数;②函数y=f(2x)反解得2x=f
-1(y),即
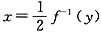
,
∴y=f(2x)的反函数为
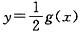
,所以②正确;③∵f(x)是奇函数,则f(-x)=-f(x),又
f(x)=f(2-x),∴-f(-x)=f(2-x),即f(x+2)=-f(x),∴f(x+4)=-f(x+2),
6. 某人要作一个三角形,要求它的三条高的长度分别是
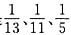
,则此人将
.
- A.不能作出满足要求的三角形
- B.作出一个锐角三角形
- C.作出一个直角三角形
- D.作出一个钝角三角形
A B C D
D
[解析] 设三角形三边长为a,b,c.根据三角形面积公式得
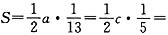
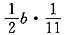
,∴a=26S,c=10S,b=22S.由大角对大边知26S对应的角最大,
∴
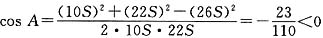
.
又A∈(0,π),∴∠A为钝角,∴D正确.
二、填空题1. 设函数
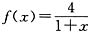
,若f(a)=2,则实数a=______.
1
[解析]
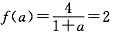
,解得:a=1.
2. 已知指数不等式(a
2+2a+5)3x>(a
2+2a+5)
1-x,则x的取值范围是______.
[解析] ∵a
2+2a+5=(a+1)
2+4≥4>1,
∴函数y=(a
2+2a+5)
x在(-∞,+∞)上是增函数,
∴3x>1-x,解得
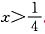
.∴x的取值范围是

.
3. 若直线x-2y+5=0与直线2x+my-6=0互相垂直,则实数m=______.
1
[解析] 因为直线x-2y+5=0与直线2x+my-6=0互相垂直,所以(1,-2)(2,m)=2-2m=0,m=1.
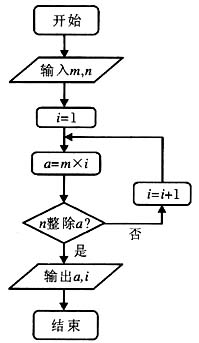
4. 阅读下面的程序框图,若输入m=4,n=6,则输出a=______,i=______.
(注:框图中的赋值符号“=”也可以写成“←”)
12 3
[解析] 输入m=4,当i=1,则a=m×i=4,但6不整除4;第一次循环之后,i=1+1=2,a=4×2=8,但6不整除8;第二次循环之后,i=2+1=3,a=4×3=12,此时6整除12,满足输出条件,输出a为12,i为3.
5. 某商家一月份至五月份累计销售额达3860万元,预测六月份销售额为500万元,七月份销售额比六月份递增x%,八月份销售额比七月份递增x%,九、十月份销售总额与七、八月份销售总额相等,若一月至十月份销售总额至少达7000万元,则x的最小值为______.
20
[解析] 依题意得:3860+500+2[500(1+x%)+500(1+x%)2]≥7000,化简得:(x%)2+3·x%≥0.64,根据二次函数的性质可得:x≥20.
6. 某射手射击所得环数ξ的分布列如下:
已知ξ的期望Eξ=8.9,则y的值为______.
0.4
[解析] x+0.1+0.3+y=1,即x+y=0.6. ①
又7x+0.8+2.7+10y=8.9,化简得7x+10y=5.4. ②
由①②联立解得x=0.2,y=0.4.
三、计算题1. 设二次函数f(x)=x
2+ax+a,方程f(x)=x的两根x
1和x
2满足0<x
1<x
2<1.
(1)求实数a的取值范围;
(2)试比较f(0)f(1)-f(0)与
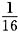
的大小,并说明理由.
解:(1)令g(x)=f(x)-x=x
2+(a-1)x+a,则由0<x
1<x
2<1得,
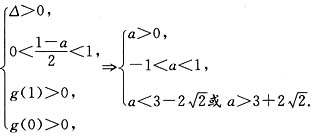
∴
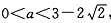
,∴实数a的取值范围是
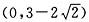
.
(2)f(0)f(1)-f(0)=2a
2,
设h(a)=2a
2,∵当a>0时,h(a)单调递增,
∴
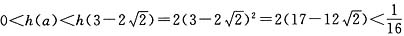
.
2. 已知函数
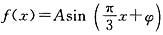
,x∈R,A>0,
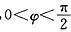
.y=f(x)的部分图象如下图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).

(1)求f(x)的最小正周期及
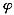
的值;
(2)若点R的坐标为(1,0),

,求A的值.
解:(1)由题意得,
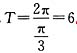
.
因为P(1,A)在
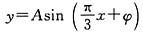
的图象上,
所以
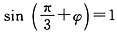
.
又因为
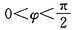
,
所以
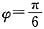
.
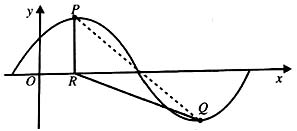
(2)设点Q的坐标为(x
0,-A).
由题意可知
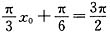
,得x
0=4,所以Q点的坐标为(4,-A).连接PQ,在△PRQ中,

,由余弦定理得:
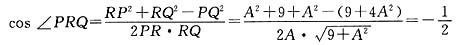
,
解得A
2=3.
又因为A>0,所以
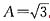
.
四、应用题1. 某车间甲组有10名工人,其中有4名女工人;乙组有5名工人,其中有3名女工人.现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组中共抽取3名工人进行技术考核.
(1)求从甲、乙两组各抽取的人数;
(2)求从甲组抽取的工人中恰有1名女工人的概率;
(3)记ξ表示抽取的3名工人中男工人数,求ξ的分布列及数学期望.
解:(1)由于甲组有10名工人,乙组有5名工人,根据分层抽样原理,若从甲、乙两组中共抽取3名工人进行技术考核,则从甲组抽取2名工人,乙组抽取1名工人.
(2)记A表示事件:从甲组抽取的工人中恰有1名女工人,则
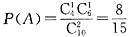
.
(3)ξ的可能取值为0,1,2,3.
A表示事件:从甲组抽取的2名工人中恰有i名男工人,i=0,1,2.
B表示事件:从乙组抽取的是1名男工人.
A
i与B独立,i=0,1,2.
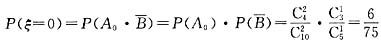
,
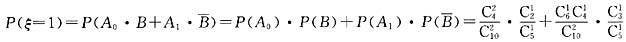
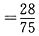
,
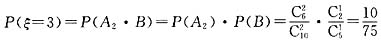
,

.
故ξ的分布列为:
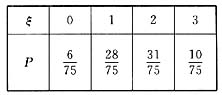
期望值为:
Eξ=0×P(ξ=0)+1×P(ξ=1)+2×P(ξ=2)+3×P(ξ=3)=
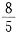
.
 故本题应选A.
故本题应选A.
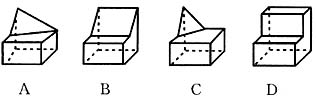
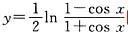 与
与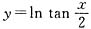 是同一函数;
是同一函数;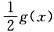 的图象也关于直线y=x对称;
的图象也关于直线y=x对称;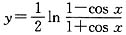 的定义域满足
的定义域满足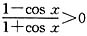 ,即cosx≠±1,x≠kπ(k∈Z),
,即cosx≠±1,x≠kπ(k∈Z),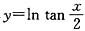 的定义域满足
的定义域满足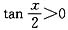 ,即
,即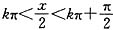 ,2kπ<x<2kπ+π(k∈Z),两函数定义域不相同,不是同一函数;②函数y=f(2x)反解得2x=f-1(y),即
,2kπ<x<2kπ+π(k∈Z),两函数定义域不相同,不是同一函数;②函数y=f(2x)反解得2x=f-1(y),即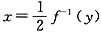 ,
,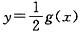 ,所以②正确;③∵f(x)是奇函数,则f(-x)=-f(x),又
,所以②正确;③∵f(x)是奇函数,则f(-x)=-f(x),又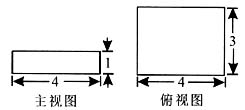
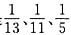 ,则此人将 .
,则此人将 .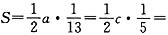
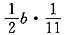 ,∴a=26S,c=10S,b=22S.由大角对大边知26S对应的角最大,
,∴a=26S,c=10S,b=22S.由大角对大边知26S对应的角最大,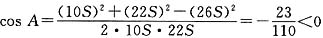 .
.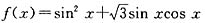 在区间
在区间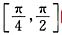 上的最大值是 .
上的最大值是 .
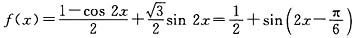 ,因为
,因为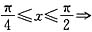
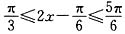 ,所以
,所以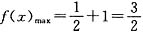 .故选C.
.故选C.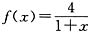 ,若f(a)=2,则实数a=______.
,若f(a)=2,则实数a=______.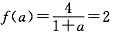 ,解得:a=1.
,解得:a=1.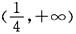
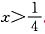 .∴x的取值范围是
.∴x的取值范围是 .
.
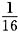 的大小,并说明理由.
的大小,并说明理由.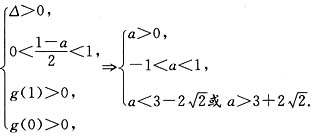
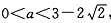 ,∴实数a的取值范围是
,∴实数a的取值范围是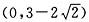 .
.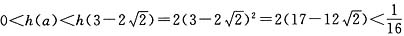 .
.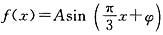 ,x∈R,A>0,
,x∈R,A>0,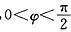 .y=f(x)的部分图象如下图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).
.y=f(x)的部分图象如下图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).
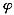 的值;
的值; ,求A的值.
,求A的值.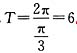 .
.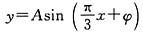 的图象上,
的图象上,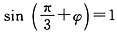 .
.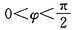 ,
,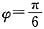 .
.
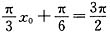 ,得x0=4,所以Q点的坐标为(4,-A).连接PQ,在△PRQ中,
,得x0=4,所以Q点的坐标为(4,-A).连接PQ,在△PRQ中, ,由余弦定理得:
,由余弦定理得: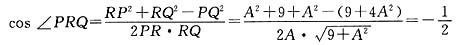 ,
,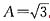 .
.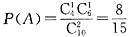 .
.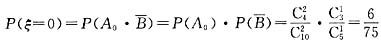 ,
,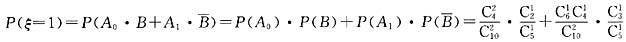
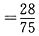 ,
,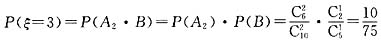 ,
, .
.
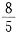 .
.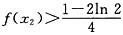 .
.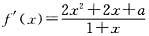 ,且f′(x)=0有两个不同的根x1、x2,
,且f′(x)=0有两个不同的根x1、x2,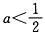 ,
,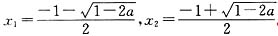 .
.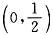 .
.
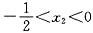 ,a=-2x2(1+x2),
,a=-2x2(1+x2),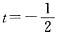 时,g′(t)=0;当
时,g′(t)=0;当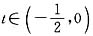 时,g′(t)>0,
时,g′(t)>0,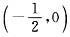 内是增函数.
内是增函数.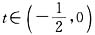 时,
时,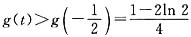 .
.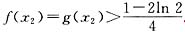 .
.