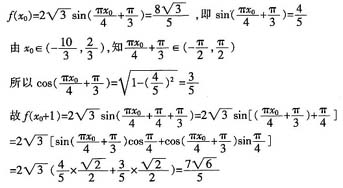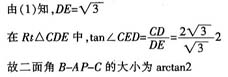一、填空题1. 若
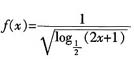
,则f(x)的定义域为______。
2. 函数
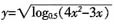
的定义域为______。
[解析] 由题意得log
0.5(4x
2-3x)≥0,则由对数函数性质得0<4x
2-3x≤1,即
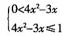
。求得函数的定义域为:
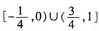
。
3. 已知椭圆G的中心在坐标原点,长轴在x轴上,离心率为
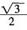
,且G上一点到G的两个焦点的距离之和为12,则椭圆G的方程为______。
[解析] 根据椭圆定义及离心率定义算得a=6,b=3,进而得到椭圆的方程。
4. 已知|a|=|b|=2,(a+2b)·(a-b)=-2,则a与b的夹角为______。
[解析] 根据两个向量数量积的定义求得它们夹角的余弦值。
5. 若直线l
1:
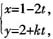
(t为参数)与直线
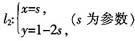
垂直,则k=______。
-1
[解析] l
1斜率为
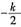
,l
2斜率为-2,两直线斜率之积为-1,故k=-1。
6. {a
n}为等差数列,已知a
1+a
2+a
3=-24,a
11+a
13+a
15=42,则a
19=______。
26
[解析] an为等差数列,则a1+a2+a3=3a1+3d=-24,a11+a13+a15=3a1+36d=42,解得a1=-10,d=2,则a19=a1+18d=26。
7. 若不等式|kx-4|≤2的解集为{x|1≤x≤3},则实数k______。
2
[解析] 由|kx-4|≤2可得-2≤kx-4≤2,即2≤kx≤6,而1≤x≤3,所以k=2.
8. log
34·log
48·log
8m=log
416,则m为______。
9
[解析] 应用对数函数的性质。
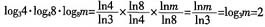
,则m=9。
9. 高度不一的五人排成一排,恰巧中间的人最高,五人中两端人都比相邻的人矮的概率为______。
[解析] 高度不一的五人排成一排的排列为
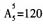
,设此五人分别为1、2、3、4、5,且身高1<2<3<4<5,由题意可知,5恰巧在中间位置,五人中两端人都比相邻的人矮,分情况:
若1在最左端,则有
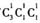
种情况;
若2在最左端,则有
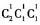
种情况;
若3在最左端,则有
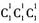
种情况;
故五人中两端人都比相邻的人矮的情况有
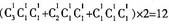
,因此,所求概率为
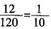
。
10. 在一次英语考试中,全班平均75分,女生的平均分比男生高14分,班里男生人数比女生多80%,则男生的平均分为______。
70
[解析] 设班上女生人数为a,则男生人数a(1+80%),设男生平均分为x分,则女生平均分为x+14,则由全班平均分为75分,可列方程为
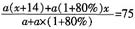
,求得x=70 。
11. 已知m,n是有理数,且方程x
2+mx+n=0有一个根是
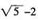
,那么m+n的值______。
3
[解析] 由m,n,均为有理数可知另一根为
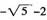
,则m=4,n=-1;m+n=3。
12. 不等式|2x-4|<|x-1|+|x-3|的解集为______。
(1,3)
[解析] 原式可化简为2|x-2|-|x-1|-|x-3|<0,则有
x<1时,原不等式化为2×(2-x)-(1-x)-(3-x)<0,无解;
1<x<2,原不等式化为2×(2-x)-(x-1)-(3-x)<0,解得1<x<2;
2<x<3,原不等式化为2×(x-2)-(x-1)-(3-x)<0,解得2<x<3;
x>3,原不等式化为2×(x-2)-(x-1)-(x-3)<0,无解;
且x=1时,2×|1-2|-|1-1|-|1-3|=0,不等式不成立:
x=2时,2×|2-2|-|2-1|-|2-3|<0,不等式成立;
x=3时,2×|3-2|-|3-1|-|3-3|=0不等式不成立:
故解集为(1,3)。
13. 已知不等式ax
2+bx+2>0的解是
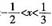
,则a+b的值______。
-14
[解析] ax
2+bx+2>0的解是
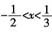
等价于ax
2+bx+2=0的解是
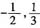
,则有
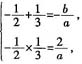
解得

14. 小波通过做游戏的方式来确定周末活动,他随机地往单位圆内投掷一点,若此点到圆心的距离大于
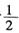
,则周末去看电影;若此点到圆心的距离小于

,则去打篮球;否则,在家看书,则小波周末不在家看书的概率为______。
[解析] 间接法求解。单位圆面积为π·1
2=π,在家看书所占面积为
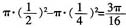
,则不在家看书的概率为

。
15. 已知点P分有向线段
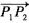
所成的比为
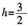
,且点P
1,P的坐标分别是(-3,2),(1,-2),则点P
2的坐标______。
[解析] 设点P
2的坐标(x,y),因为
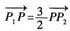
,则
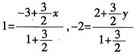
,解得
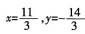
,点P
2的坐标为
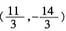
。
二、选择题(在每小题4个备选答案中,选出一个符合题意的正确答案。)
1. 已知命题p:
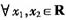
,(f(x
2)-f(x
1))(x
2-x
1)≥0,则-p是
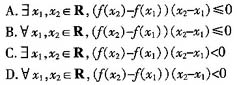
A B C D
C
[解析] 命题p为全称命题,所以其否定p应是特称命题,又(f(x2)-f(x1))(x2-x1)≥0否定为f((x2)-f(x1))(x2-x1)<0,故选C。
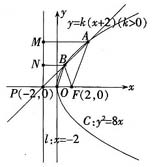
4. 已知直线y=k(x+2)(k>0)与抛物线C:y
2=8x相交于A、B两点,F为C的焦点,若|FA|=2|FB|,则k=

A B C D
D
[解析] 设抛物线C:y
2=8x的准线为l:x=-2,直线y=k(x+2)(k>0)恒过定点P(-2,0)。如图过A、B分别作AM⊥l于M,BN⊥l于N,由|FA|=2|FB|,则|AM|=2|BN|,点B为AP的中点。连结OB,则

,则|OB|=|BF|,点B的横坐标为1,故点B的坐标为
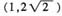
,所以k=
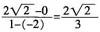
。
三、解答题1. 已知sinA+sinC=psinB(p∈R),且
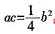
。
(1)当
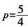
,b=1时,求a,c的值;
(2)若角B为锐角,求p的取值范围;
(1)由题设并利用正弦定理,得

(2)由余弦定理,
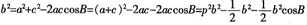
,即
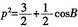
,因为0<cosB<1,得
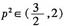
,由题设知p>0,所以
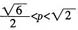
。
2. 某射手每次射击击中目标的概率是

,且各次射击的结果互不影响。
(1)假设这名射手射击5次,求恰有2次击中目标的概率;
(2)假设这名射手射击5次,求有3次连续击中目标,另外2次未击中目标的概率。
(1)设x为射手在5次射击中击中目标的次数,则
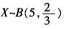
。在5次射击中,恰有2次击中目标的概率
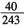
。
(2)设“第i次射击击中目标”为事件A
i(i=1,2,3,4,5);“射手在5次射击中,有3次连续击中目标,另外2次未击中目标”为事件A,则
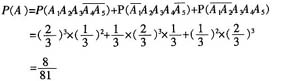
3. 函数

在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形。
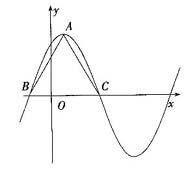
(1)求ω的值及函数f(x)的值域;
(2)
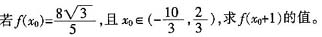
4. 如图,在三棱锥P-ABC中,∠APB=90°,∠PAB=60°,AB=BC=CA,平面PAB⊥平面ABC。
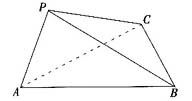
(1)求直线PC与平面ABC所成角的大小;
(2)求二面角B-AP-C的大小。
(1)设AB的中点为D,AD的中点为O,连接PO、CO、CD,由已知,△PAD为等边三角形,
所以PO⊥AD
又平面PAB⊥平面ABC,平面PAB∩平面ABC=AD,
所以PO⊥平面ABC
所以∠OCP为直线PC与平面ABC所成的角


(2)过D作DE⊥AP于E,连接CE
由已知可得,CD⊥平面PAB
根据三垂线定理知,CD⊥PA
所以∠CED为二面角B-AP-C的平面角
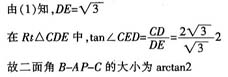

五、教学设计题1. 根据下面给出的题目,编写出科学可行的教学片段。
试编写《圆的认识》一课的教学片段。
教学片段:
师:同学们认识了哪些平面图形?
生:我们认识了长方形、正方形、平行四边形、三角形、梯形。
师:这些平面图形都有一个共同的特点,你知道吗?
生:它们都是由线段围成的平面图形。
师:有没有不是线段围成的平面图形呢?
生:有,比如圆。
师:对,圆是平面上的一种曲线图形,不是由线段围成,那么今天我们就一起来探究平面上的曲线图形——圆。
师:你想知道有关圆的哪些知识?
生:我想知道什么是圆?圆各部分的名称、圆的周长在哪里?怎样求圆的周长、圆的面积?
师:今天我们满足同学们的部分要求,先认识圆,后面再学习周长和面积。相信通过今天的学习,同学们会找到满意的答案。
什么是圆呢?书上已明确地告诉了我们。请打开书阅读第一自然段。
师:同学们知道什么是圆了。找一找,生活中哪些物体是圆形的?
生:硬币、钟面、桌面、茶杯口、饮料瓶底、圆柱的底面…
师:观察得非常仔细。现在老师想把这些圆形画在纸上,能帮老师想想办法吗?四人小组一起商量商量,有哪些办法可以把圆画在纸上?
谁愿意把你想的好办法说给大家听听?
生1:可以用圆规画圆。
生2:可以将瓶底或茶杯放在纸上,沿边画下就是一个圆。
生3:可以用一段线、一支铅笔,将线的一端按住不动,另一端绕上铅笔,在纸上画一圈,就得到一个圆。
师:同学们想的办法真好!那什么方法又快又好呢?
生:将茶杯倒扣在纸上,沿边画一周,又快又好。
师:用又快又好的办法把圆画在纸上,然后剪下。
(紧接着,在认识圆时,又开展了下列活动。)
师:同学们,拿出刚才剪下的圆,我们一起动手来折一折。先对折,打开,换方向对折,打开,再换方向对折,打开,重复几次。
观察圆上的折痕,发现了什么?
生:这些折痕都相交于一点。
师:相交的这一点在哪里?
生:在圆的中心。
师:我们把圆中心的这一点叫做圆心,一般用字母O表示。请同学们在剪下的圆中,找到圆心,标上字母O。
师:请同学们将圆心到圆上任意一点连接起来,想一想,能连多少条?
师:我们把刚才连接圆心到圆上任意一点的线段叫做圆的半径,一般用字母r表示。在剪下的圆中标出半径r。
师:那么,在同一个圆里,有多少条半径?
生:在同一个圆里,有无数条半径。
师:拿出直尺,量一量这些半径,你有什么发现?
生:
师:把两次发现大胆告诉同学们。
生:在同一个圆里,有无数条半径,每条半径都相等。
……
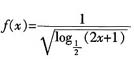 ,则f(x)的定义域为______。
,则f(x)的定义域为______。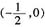
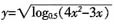 的定义域为______。
的定义域为______。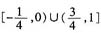
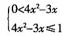 。求得函数的定义域为:
。求得函数的定义域为: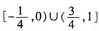 。
。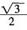 ,且G上一点到G的两个焦点的距离之和为12,则椭圆G的方程为______。
,且G上一点到G的两个焦点的距离之和为12,则椭圆G的方程为______。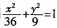
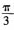
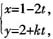 (t为参数)与直线
(t为参数)与直线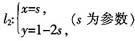 垂直,则k=______。
垂直,则k=______。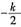 ,l2斜率为-2,两直线斜率之积为-1,故k=-1。
,l2斜率为-2,两直线斜率之积为-1,故k=-1。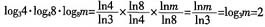 ,则m=9。
,则m=9。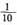
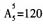 ,设此五人分别为1、2、3、4、5,且身高1<2<3<4<5,由题意可知,5恰巧在中间位置,五人中两端人都比相邻的人矮,分情况:
,设此五人分别为1、2、3、4、5,且身高1<2<3<4<5,由题意可知,5恰巧在中间位置,五人中两端人都比相邻的人矮,分情况: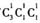 种情况;
种情况;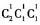 种情况;
种情况;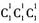 种情况;
种情况;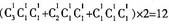 ,因此,所求概率为
,因此,所求概率为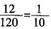 。
。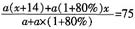 ,求得x=70 。
,求得x=70 。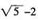 ,那么m+n的值______。
,那么m+n的值______。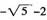 ,则m=4,n=-1;m+n=3。
,则m=4,n=-1;m+n=3。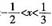 ,则a+b的值______。
,则a+b的值______。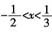 等价于ax2+bx+2=0的解是
等价于ax2+bx+2=0的解是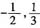 ,则有
,则有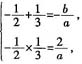

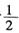 ,则周末去看电影;若此点到圆心的距离小于
,则周末去看电影;若此点到圆心的距离小于 ,则去打篮球;否则,在家看书,则小波周末不在家看书的概率为______。
,则去打篮球;否则,在家看书,则小波周末不在家看书的概率为______。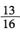
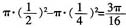 ,则不在家看书的概率为
,则不在家看书的概率为 。
。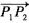 所成的比为
所成的比为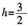 ,且点P1,P的坐标分别是(-3,2),(1,-2),则点P2的坐标______。
,且点P1,P的坐标分别是(-3,2),(1,-2),则点P2的坐标______。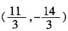
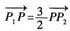 ,则
,则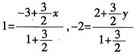 ,解得
,解得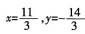 ,点P2的坐标为
,点P2的坐标为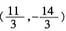 。
。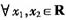 ,(f(x2)-f(x1))(x2-x1)≥0,则-p是
,(f(x2)-f(x1))(x2-x1)≥0,则-p是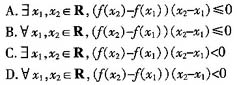
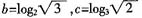 ,则
,则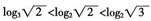 ,所以b>c。又因为
,所以b>c。又因为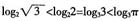 ,故a>b,所以a>b>c,故选A。
,故a>b,所以a>b>c,故选A。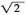 ,则以该正方体各个面的中心为顶点的凸多面体的体积为
,则以该正方体各个面的中心为顶点的凸多面体的体积为
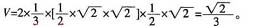

 ,则|OB|=|BF|,点B的横坐标为1,故点B的坐标为
,则|OB|=|BF|,点B的横坐标为1,故点B的坐标为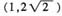 ,所以k=
,所以k=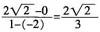 。
。
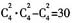 种。
种。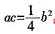 。
。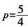 ,b=1时,求a,c的值;
,b=1时,求a,c的值;
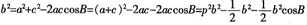 ,即
,即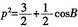 ,因为0<cosB<1,得
,因为0<cosB<1,得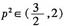 ,由题设知p>0,所以
,由题设知p>0,所以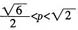 。
。 ,且各次射击的结果互不影响。
,且各次射击的结果互不影响。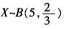 。在5次射击中,恰有2次击中目标的概率
。在5次射击中,恰有2次击中目标的概率 。
。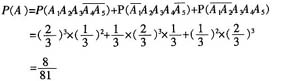
 在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形。
在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形。
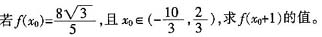
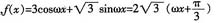

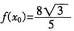 ,由(1)有
,由(1)有