一、选择题1. 设函数f(x)具有连续导数,且
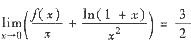
,则
- A.f(0)=0且f'(0)=2.
- B.f(0)=0且f'(0)=1.
- C.f(0)=-1且f'(0)=2.
- D.f(0)=-1且f'(0)=1.
A B C D
C
[解析] 求出f(x)带皮亚诺余项的麦克劳林公式解本题.由极限与无穷小的关系得

其中

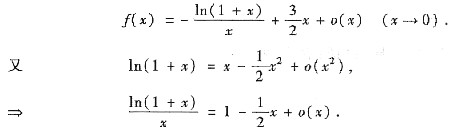
代入得

因此,f(0)=-1,f'(0)=2,应选(C).
[分析二] 利用带皮亚诺余项的麦克劳林公式求解本题.把
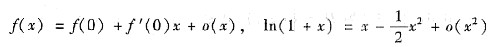
代入题设的极限,可得
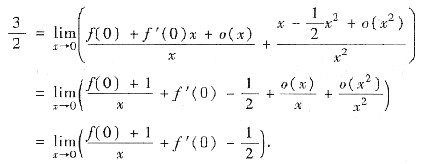
从而f(0)+1=0,

,即f(0)=-1,f'(0)=2.故应选(C).
[分析三] 利用极限的运算法则,导数的定义与洛必达法则来求解本题.由题设可知
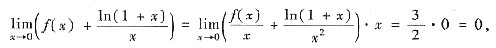
从而
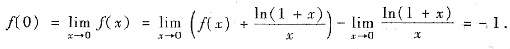
又

故应选(C).
2. 若一条二次曲线把(-∞,0)内的曲线段e
x和(1,+∞)内的曲线段
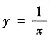
连接成一条一阶可导的曲线,则定义在[0,1]上的这条二次曲线为
- A.y=-2x2+2x+1.
- B.y=-x2-x+1.
- C.y=-x2+x+1.
- D.y=x2-x+1.
A B C D
C
[解析] 设所求二次曲线为y=ax
2+bx+c(0≤x≤1),则依题设有
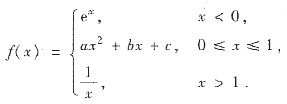
由f(x)的连续性,在x=0点有e
0=c
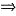
c=1.
在x=1点有a+b+c=1
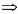
a+b=0.
由f(x)一阶可导,且f'
+(0)=b,f'
-(0)=e
0=I,故b=1,从而还有a=-1.
于是y=-x
2+x+1.所以选项(C)正确.
经验算可知对点x=1,选项(C)也正确.
4. 设f(x),g(x)在x=0的某邻域内连续,f(0)=g(0)≠0,又设

,
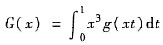
,则当x→0时,F(x)是G(x)的
- A.同阶但不等价无穷小.
- B.等价无穷小.
- C.高阶无穷小.
- D.低阶无穷小.
A B C D
B
[解析]
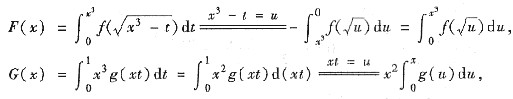
由于
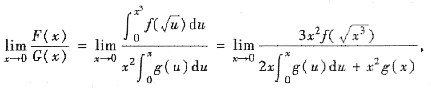
又
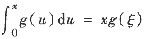
,其中ξ在0与x之间,当x→0时,ξ→0,所以
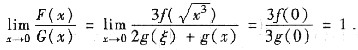
故F(x)是G(x)的等价无穷小,选(B).
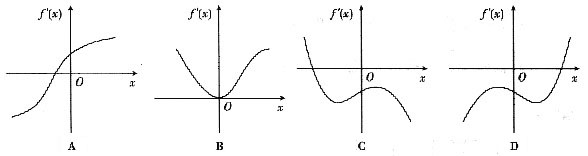
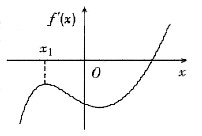
5. 设f(x)二阶可导,且存在极小值点和拐点,则f'(x)的图形可以是
A B C D
D
[解析] 由于f(x)二阶可导,且具有极小值,故存在一点x
0,使f'(x
0)=0,f"(x
0)>0,满足这一条件的有(A)、(D),故排除(B)、(C).又f(x)的图形有拐点,故应存在一点x
1,使得f"(x
1)=0,且在x
1的左右二阶导数异号,可见(A)不具备这样的点,而(D)中的x
1具有该性质(如右图),故选(D).
6. 设
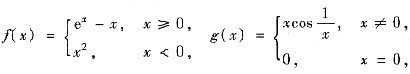
则下面四个命题
① f(x)在[-1,1]上存在原函数 ② g(x)在[-1,1]上存在原函数
③ 存在定积分
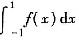
④ g'(0)存在
中正确的是
(A) ①,②. (B) ②,③. (C) ①,②,③.(D) ②,③,④.
A B C D
B
[解析] 由于f(x)在[-1,1]上不连续,从而不存在原函数,故①不正确.由于g(x)在[-1,1]上连续,故存在原函数,所以②正确.
由于
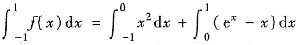
都存在,故③正确.
由于
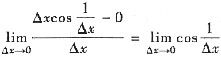
不存在,所以g(x)在x=0处不可导,即g'(0)不存在,故④不正确.
综上所述,②、③正确,故选(B).
7. 设f(x)在(-∞,+∞)内可导,且
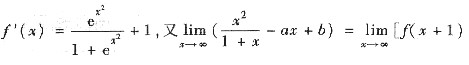
-f(x)],则
- A.a=1,b=3.
- B.a=2,b=2.
- C.a=-1,b=3.
- D.a=3,b=-1.
A B C D
A
[解析] 由拉格朗日中值定理,有
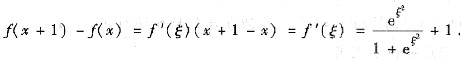
当x→∞时,ξ→∞,于是
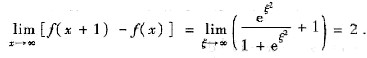
由于
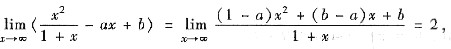
则有
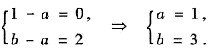
故选(A).
8. 下列反常积分

中收敛的是
A B C D
D
[解析] 由于
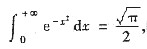
故①收敛.
由于
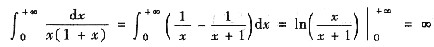
,故②发散.
由于
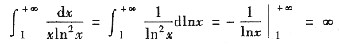
,故③发散.
由于
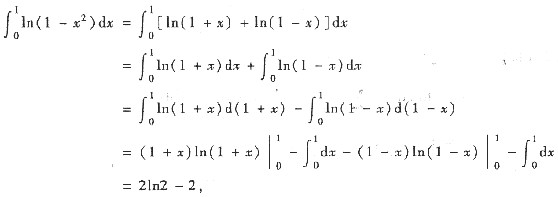
故④收敛.
综上分析,可知应选(D).
二、填空题1.
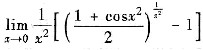
=______.
2. 设

,则
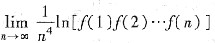
=______.
[解析] 化为定积分求极限,则
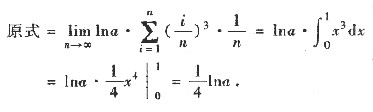
4.
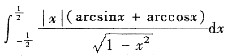
=______.
[解析]

5. 设f(x)二阶可导,且

,则f(0)=______.
6
[解析]
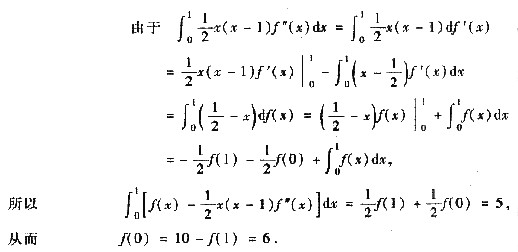
6. 差分方程y
t+1-2y=(3t-4)2
t的通解是______.
[解析] 设差分方程的通解为y
t=c·2
t+(At
2+Bt)·2
t,其中A,B为待定常数,C为任意常数,于是y
t+1=C·2
t+1=(At
2+2At+A+Bt+B)·2
t+1,代入方程可得
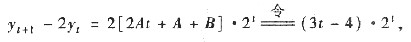
由此可得
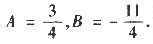
即所求的通解为
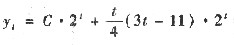
7. 设x=rcosθ,y=rsinθ,把极坐标系中的累次积分
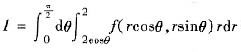
转化为直角坐标系中的累次积分可得I=______.
8. 交换积分顺序
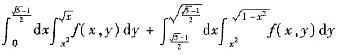
=______.
[解析]
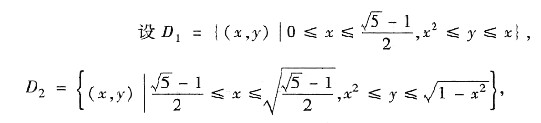
且D=D
1+D
2,则

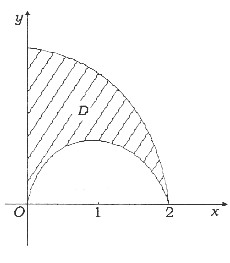
其中积分区域D如图所示.由于D关于直线y=x对称,故交换积分次序即得
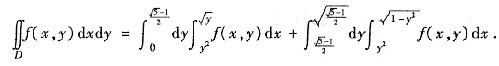

三、解答题1. 设f(x)在x=0邻域有连续的导数,又
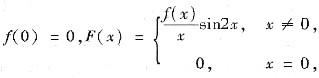
求证:F(x)在x=0有连续导数.
[分析与证明一] 先求F'(0).
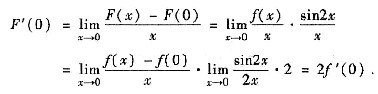
再求
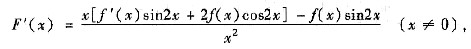
及
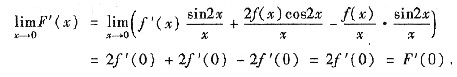
因此,F'(x)在x=0连续.
[分析与证明二] 先证F(x)在x=0连续.
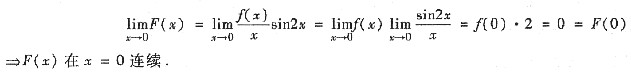
如同[证法一]
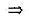
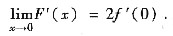
于是F'(0)=2f'(0),F'(x)在x=0连续.
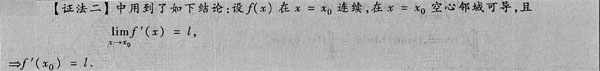
2. 设函数f(x)在x=1的某邻域内连续,且有
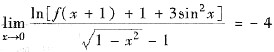
.
(Ⅰ) 求f(1)及f'(1);
(Ⅱ) 设f"(1)存在,求f"(1);
(Ⅲ) x=1是否是f(x)的极值点?若是,是极大值点还是极小值点?
[分析与求解] (Ⅰ) 由条件知,
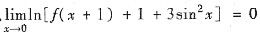
.
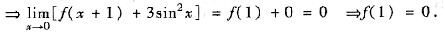
又在x=0空心邻域f(x+1)+3sin
2x≠0,现利用当x→0时的等价无穷小因子替换
ln(1+f(x+1)+3sin
2x)~f(x+1)+3sin
2x,
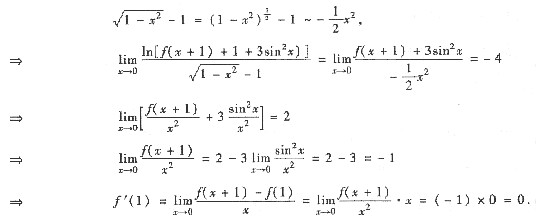
(Ⅱ)由f"(1)存在
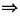
f(x)在x=1某邻域可导
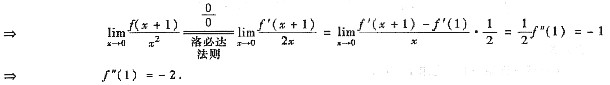
或用泰勒公式
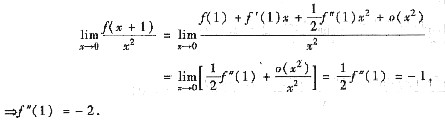
(Ⅲ) 由
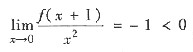
及极限的不等式性质

δ>0,当0<|x|<δ时
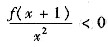
即f(x+1)<0=f(1).
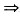
x=1是f(x)的极大值点.

3. 设函数f(u)有连续的一阶导数,f)0)=1,且函数
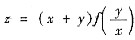
满足:
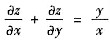
(x≠0),求z的表达式.
[解] 由于
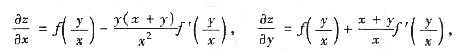
依题设有
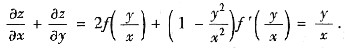
①
令
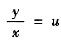
,则①式化为
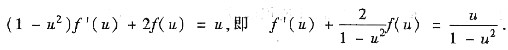
于是
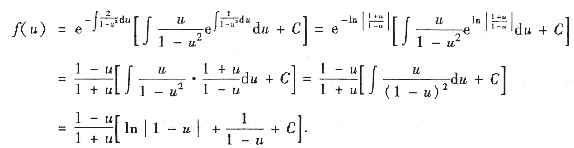
由f(0)=1可知C=0.因此
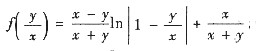
从而
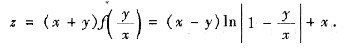
4. 设f(x)在[1,3]上连续,在(1,3)内可导,试证:存在两点ξ,η∈(1,3),使得
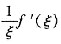
=
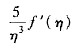
.
[证明] 取g(x)=x
2,则由题设知f(x)与g(x)都在[1,3]上连续,在(1,3)内可导,且g'(x)=2x≠0在x∈(1,3)成立,从而由柯西定理知:存在ξ∈(1,3)使得
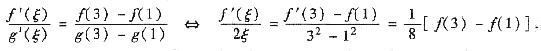
取h(x)=x
4,则由题设知f(x)与h(x)都在[1,3]上连续,在(1,3)内可导,且h'(x)=4x
3≠0在x∈(1,3)成立,从而由柯西定理知:存在η∈(1,3)使得
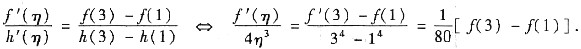
由此可得
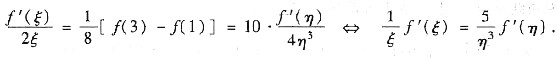
5. 计算二重积分
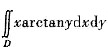
,其中
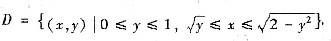
6. 求
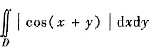
,其中区域
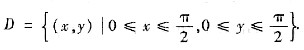
[分析与求解] 这里0≤x+y≤π,且被积函数
|cos(x+y)|
=
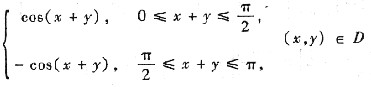
于是,用
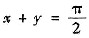
将D分成D
1,D
2两个区域,见右图.用分块积分法得
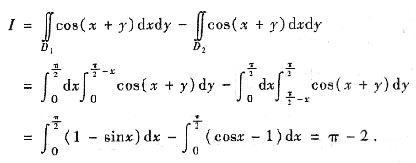

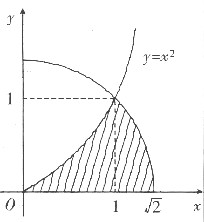
7. 设f(x,y)=max{x,y},D={(x,y)|0≤x≤1,0≤y≤1},计算
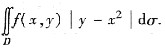
[解] 将D={(x,y)|0≤x≤1,0≤y≤1}分成
D
1={(x,y)|0≤x≤y≤1}与D
2={(x,y)|0≤y≤x≤1}.
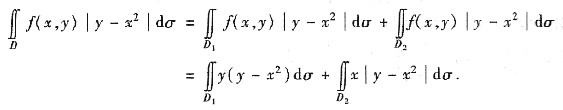
但D
2又可分为曲线y=x
2上方及下方两块,于是
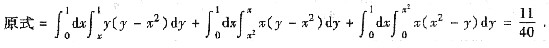
8. (Ⅰ) 将累次积分

化成定积分,其中a>0为常数;
(Ⅱ) 求

.
[分析与求解] (Ⅰ) I(a)是二重积分的一个累次积分,令
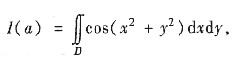
其中D={(x,y)|0≤x≤2a,

,它是半圆域,如图,设x=raosθ,y=rsinθ换为极坐标系,则
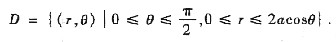
于是
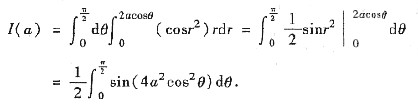

(Ⅱ) 注意当a→0时ln(1+a
2)~a
2,由二重积分中值定理知,
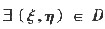
,使得
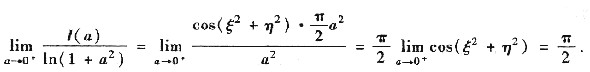
在此利用了当a→0
+时ξ
2+η
2→0,从而
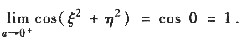
9. 设连续函数f(x)满足方程
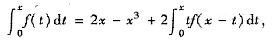
求f(x).
[解] 令u=x-t作换元,则t:0→x
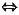
u:x→0,且t=x-u,dt=-du,代入即得
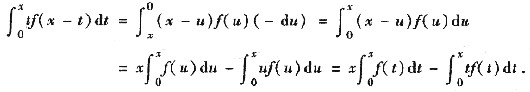
从而原方程可改写为

因f(x)连续,2x-x
3可导,故上式中各项都可导.将上式两端对x求导数,就有
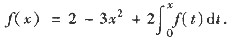
(*)
在(*)式中令x=0可得f(0)=2,又因(*)式右端各项都可导,从而f(x)可导.将(*)式两端对x求导可得
f'(x)=-6x+2f(x).
综上可知f(x)是如下一阶线性微分方程初值问题的特解
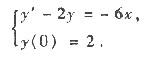
用积分因子e
-2x同乘方程两端得 (e
-2xy)'=-6xe
-2x.积分得
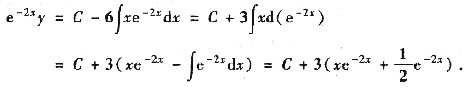
于是方程的通解是
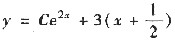
.利用初值y(0)=2可确定常数

.故所求的函数

10. 设f(x)在[0,a]有连续的一阶导数,在(0,a)二阶可导且f"(x)>0(x∈(0,a)),又f(0)=0,求证:
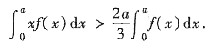
[分析与证明] 引进辅助函数
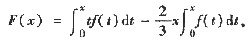
只须证明
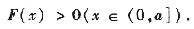
考察

特别有 F(a)>0.
11. 将函数

展开成x的幂级数.
[解] 注意
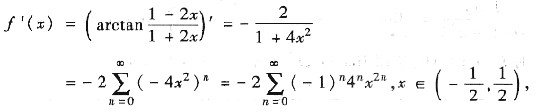
且
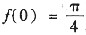
,于是,逐项积分可得
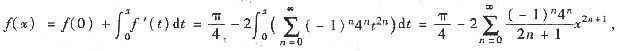
由于所得的展开式不仅在开区间
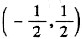
成立,而且还在两个端点
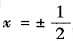
处收敛,故所得的展开式在闭区间
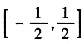
上成立.
12. 判断下列级数的敛散性,并指出收敛时是条件收敛还是绝对收敛:
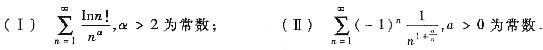
[分析与求解] (Ⅰ)
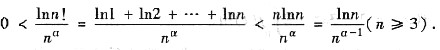
由于α>2
α-1>1,取常数P满足不等式α-1>p>1
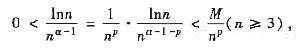
其中
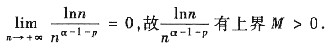
因
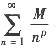
收敛,由比较判别法知,
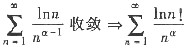
收敛,因是正项级数,故绝对收敛.
(Ⅱ) 由
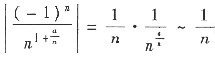
(其中
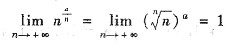
)
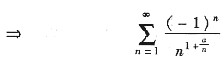
非绝对收敛.
原级数是交错级数,易知
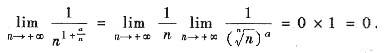
为考察
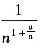
的单调性,令

则
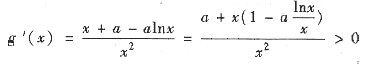
(当x充分大时)
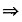
当x充分大时
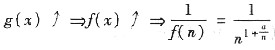
当a充分大时单调减少.由于改变有限项不改变级数的敛散性,由莱布尼兹判别法知原级数收敛,因此是条件收敛.
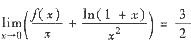 ,则
,则

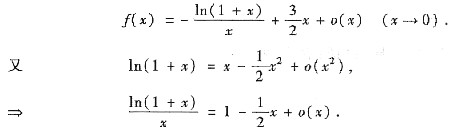

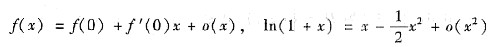
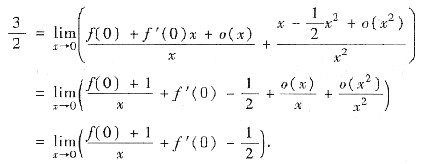
 ,即f(0)=-1,f'(0)=2.故应选(C).
,即f(0)=-1,f'(0)=2.故应选(C).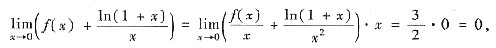
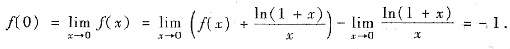

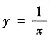 连接成一条一阶可导的曲线,则定义在[0,1]上的这条二次曲线为
连接成一条一阶可导的曲线,则定义在[0,1]上的这条二次曲线为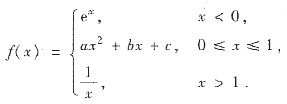
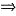 c=1.
c=1.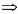 a+b=0.
a+b=0. (其中n为正整数)=
(其中n为正整数)=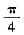 . (C)
. (C) 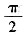 . (D) π.
. (D) π.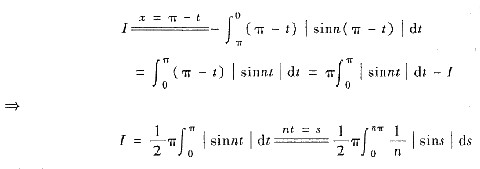
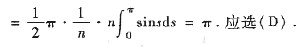
 ,
,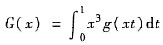 ,则当x→0时,F(x)是G(x)的
,则当x→0时,F(x)是G(x)的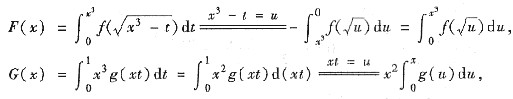
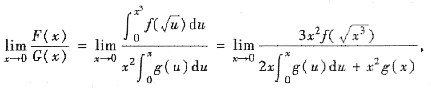
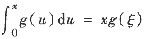 ,其中ξ在0与x之间,当x→0时,ξ→0,所以
,其中ξ在0与x之间,当x→0时,ξ→0,所以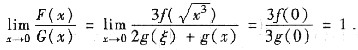


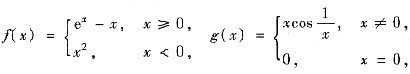 则下面四个命题
则下面四个命题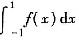 ④ g'(0)存在
④ g'(0)存在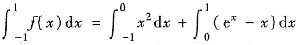 都存在,故③正确.
都存在,故③正确.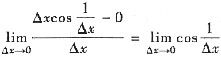 不存在,所以g(x)在x=0处不可导,即g'(0)不存在,故④不正确.
不存在,所以g(x)在x=0处不可导,即g'(0)不存在,故④不正确.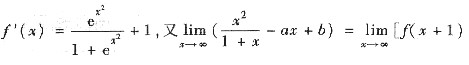 -f(x)],则
-f(x)],则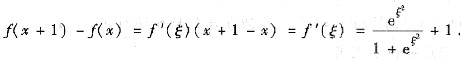
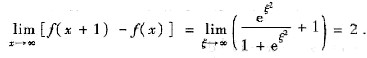
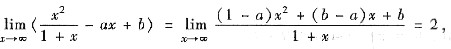
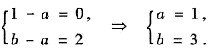 故选(A).
故选(A).
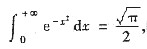 故①收敛.
故①收敛.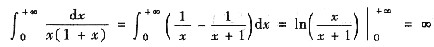 ,故②发散.
,故②发散.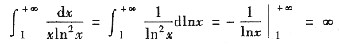 ,故③发散.
,故③发散.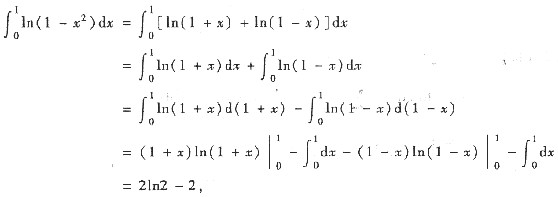
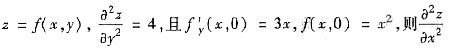 =
=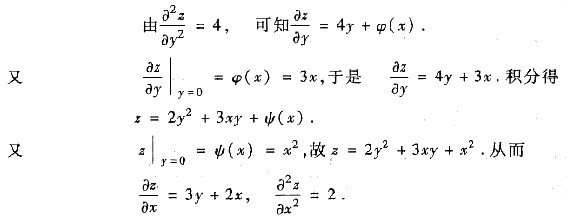
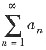 中的负项改为零,其它项保留,所成的级数记为
中的负项改为零,其它项保留,所成的级数记为 ;将级数
;将级数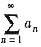 中的正项改为零,其它项保留,所成的级数记为
中的正项改为零,其它项保留,所成的级数记为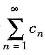 ,则下列说法正确的是
,则下列说法正确的是

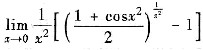 =______.
=______.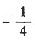
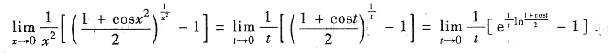

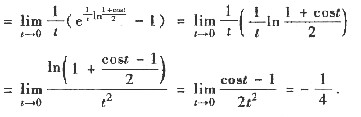
 ,则
,则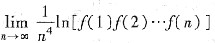 =______.
=______.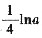
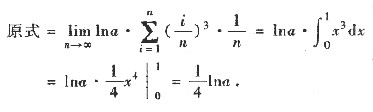
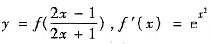 ,则
,则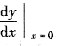 =______.
=______.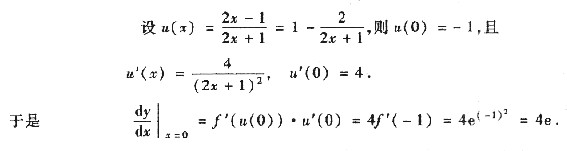
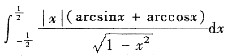 =______.
=______.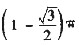

 ,则f(0)=______.
,则f(0)=______.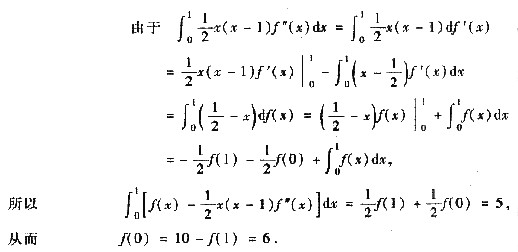
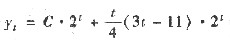
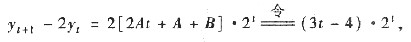
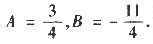 即所求的通解为
即所求的通解为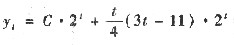
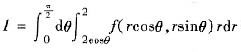 转化为直角坐标系中的累次积分可得I=______.
转化为直角坐标系中的累次积分可得I=______.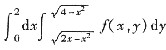

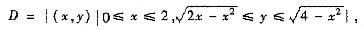

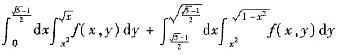 =______.
=______.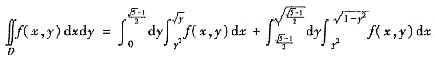
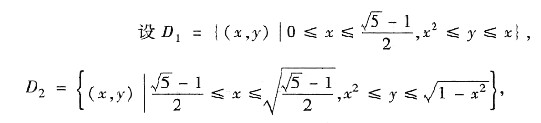

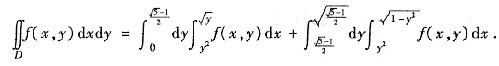

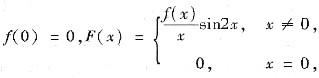 求证:F(x)在x=0有连续导数.
求证:F(x)在x=0有连续导数.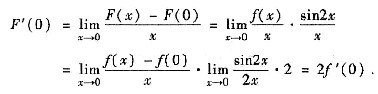
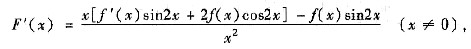
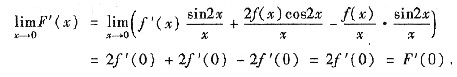
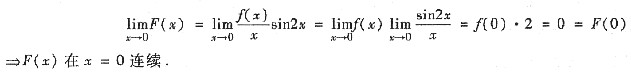
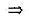
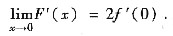
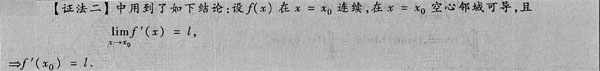
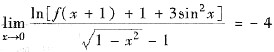 .
.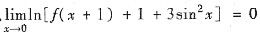 .
.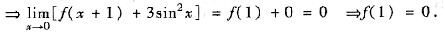
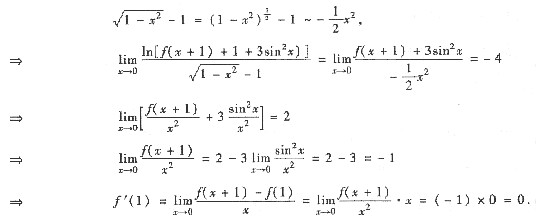
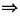 f(x)在x=1某邻域可导
f(x)在x=1某邻域可导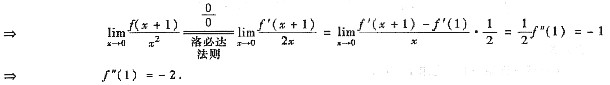
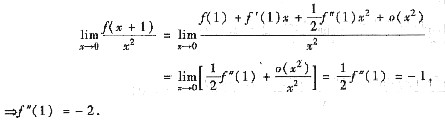
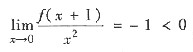 及极限的不等式性质
及极限的不等式性质 δ>0,当0<|x|<δ时
δ>0,当0<|x|<δ时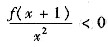 即f(x+1)<0=f(1).
即f(x+1)<0=f(1).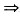 x=1是f(x)的极大值点.
x=1是f(x)的极大值点.
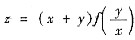 满足:
满足: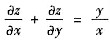 (x≠0),求z的表达式.
(x≠0),求z的表达式.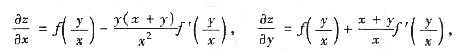
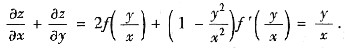 ①
①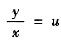 ,则①式化为
,则①式化为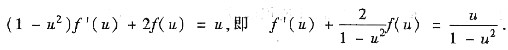
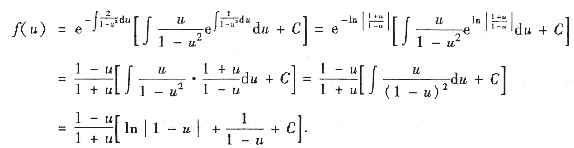
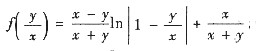
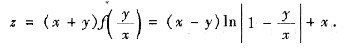
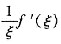 =
=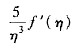 .
.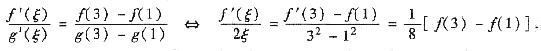
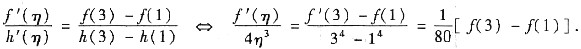
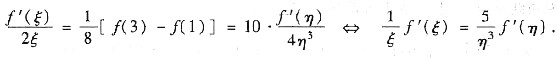
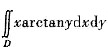 ,其中
,其中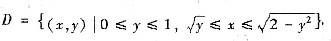

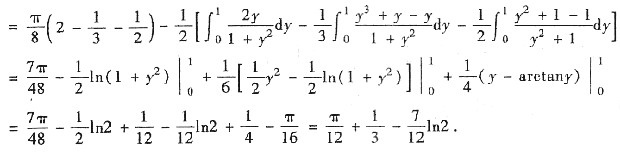
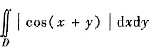 ,其中区域
,其中区域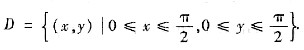
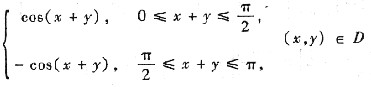
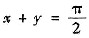 将D分成D1,D2两个区域,见右图.用分块积分法得
将D分成D1,D2两个区域,见右图.用分块积分法得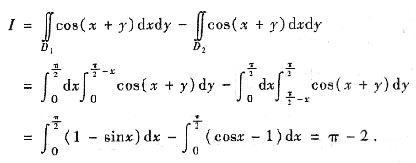

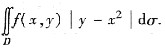
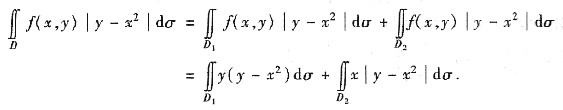
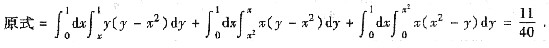
 化成定积分,其中a>0为常数;
化成定积分,其中a>0为常数; .
.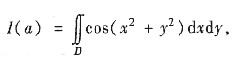
 ,它是半圆域,如图,设x=raosθ,y=rsinθ换为极坐标系,则
,它是半圆域,如图,设x=raosθ,y=rsinθ换为极坐标系,则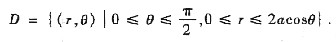
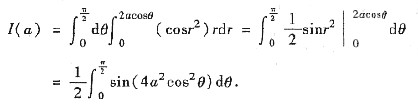

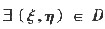 ,使得
,使得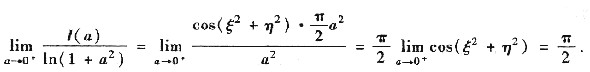
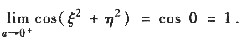
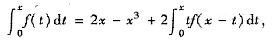 求f(x).
求f(x).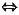 u:x→0,且t=x-u,dt=-du,代入即得
u:x→0,且t=x-u,dt=-du,代入即得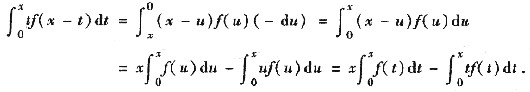

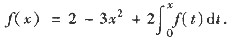 (*)
(*)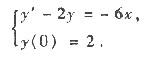
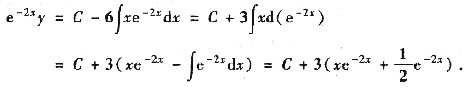
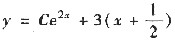 .利用初值y(0)=2可确定常数
.利用初值y(0)=2可确定常数 .故所求的函数
.故所求的函数
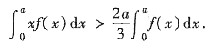
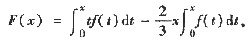
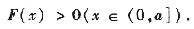

 展开成x的幂级数.
展开成x的幂级数.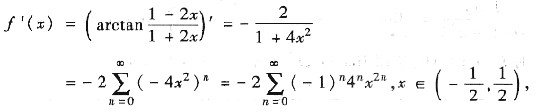
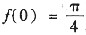 ,于是,逐项积分可得
,于是,逐项积分可得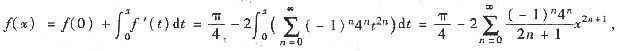
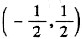 成立,而且还在两个端点
成立,而且还在两个端点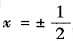 处收敛,故所得的展开式在闭区间
处收敛,故所得的展开式在闭区间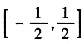 上成立.
上成立.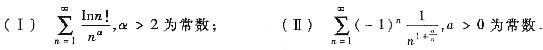
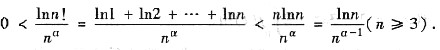
 α-1>1,取常数P满足不等式α-1>p>1
α-1>1,取常数P满足不等式α-1>p>1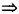
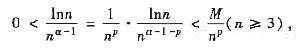
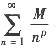 收敛,由比较判别法知,
收敛,由比较判别法知,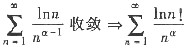 收敛,因是正项级数,故绝对收敛.
收敛,因是正项级数,故绝对收敛.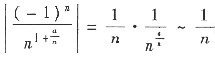 (其中
(其中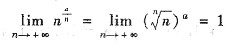 )
)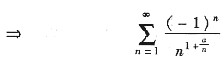 非绝对收敛.
非绝对收敛.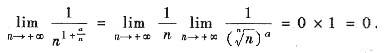
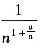 的单调性,令
的单调性,令
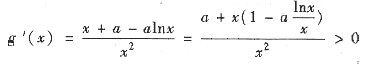
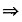 当x充分大时
当x充分大时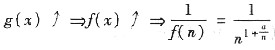 当a充分大时单调减少.由于改变有限项不改变级数的敛散性,由莱布尼兹判别法知原级数收敛,因此是条件收敛.
当a充分大时单调减少.由于改变有限项不改变级数的敛散性,由莱布尼兹判别法知原级数收敛,因此是条件收敛.