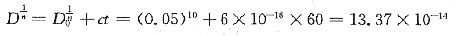论述题1. 有一根长为5m、直径为3mm的铝线,已知铝的弹性模量为70GPa,求在200N的拉力作用下,此线的总长度。
在弹性范围内,应力与应变符合胡克定律σ=Eε,而
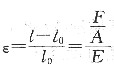
,所以
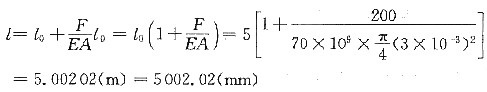
2. 一Mg合金的屈服强度为180MPa,E为45GPa,①求不至于使一块10mm×2mm的Mg板发生塑性变形的最大载荷。②在此载荷作用下,该镁板每mm的伸长量为多少?
①不发生塑性变形的最大载荷可根据应力近似等于屈服强度时来计算:
F=σ
A=180×10
6×10×2×10
-6=3600N
②
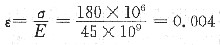
3. 已知烧结Al
2O
3的孔隙度为5%,其E=370GPa。若另一烧结Al
2O
3的E=270GPa,试求其孔隙度。
陶瓷材料的E与其孔隙体积分数φ之间的关系可用下式表示:
E=E
0(1-1.9φ+0.9φ
2)
式中E
0为无孔隙材料的弹性模量。
将已知条件代入上式,可求得
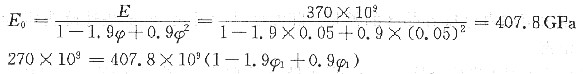
故 φ
1=19.61%
4. 有一Cu-30%Zn黄铜板冷轧25%后厚度变为1cm,接着再将此板厚度减小到0.6cm,试求总冷变形度,并推测冷轧后性能的变化。
冷变形度=
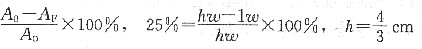
总变形度=
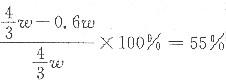
冷轧后黄铜板强度和硬度提高,而塑性、韧性降低,这就是加工硬化现象。
5. 有一截面为10mm×10mm的镍基合金试样,其长度为40mm,拉伸试验结果如下。
载荷/N | 标距长度/mm |
0 | 40.0 |
43100 | 40.1 |
86200 | 40.2 |
102000 | 40.4 |
104800 | 40.8 |
109600 | 41.6 |
113800 | 42.4 |
121300 | 44.0 |
126900 | 46.0 |
127600 | 48.0 |
113800(破断) | 50.2 |
试计算其抗拉强度σ
b、屈服强度σ
0.2、弹性模量E及延伸率δ。
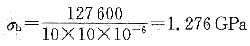
σ
0.2可以从拉伸的应力-应变曲线上求得,为1000MPa,
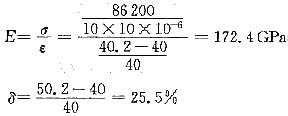
6. 将一根长为20m、直径为14mm的铝棒通过孔径为12.7 mm的模具拉拔,试求:①这根铝棒拉拔后的尺寸;②这根铝棒要承受的冷加工率。
①变形过程中,总的体积不变,设拉拔后的长度为L,则
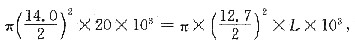
故
L=24.3m
②冷加工率即为断面收缩率
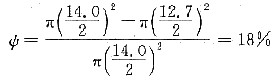
7. 确定下列情况下的工程应变ε
e和真实应变e
T,说明何者更能反映真实的变形特性:
①由L伸长至1.1L; ②由h压缩至0.9h;
③由L伸长至2L; ④由h压缩至0.5h。
①
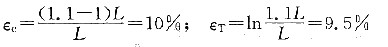
②

③
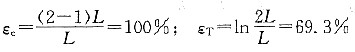
④
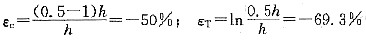
从上得知ε
T≠ε
e,变形量越大,ε
T和ε
e之间的差值就越大。比较③和④,将长度为L的均匀试样伸长1倍与压缩其长度的

,二者真实应变量的绝对值相等,而工程应变量的绝对值却不相等,所以用真实应变更能反映真实的变形特性。
8. 对于预先经过退火的金属多晶体,其真实的应力-应变曲线塑性部分可近似表示为σ
T=
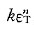
,其中k和n为经验常数,分别称为强度系数和应变硬化指数。若有A,B两种材料,其走值大致相等,而n
A=0.5,n
B=0.2,则问:①哪一种材料的硬化能力较高,为什么?②同样的塑性应变时,A和B哪个位错密度高,为什么?③导出应变硬化指数n和应变硬化率
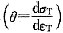
之间的数学公式。
①对
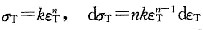
,所以
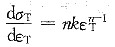
当ε
T<1时,若0<n<1,则n较大者,
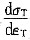
也较大,所以A比B的应变硬化能力高。
②当ε
T<1时,若O<n<1,走值大致相等,在相同的ε
T下,n越大,则σ
T越小,又σ
T∝
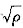
,所以n越大,ρ越小,由于A的n值比B的高,所以在同样的塑性应变时,B的位错密度高。
③
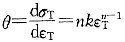
,将

代入,得
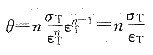
9. 有一70MPa应力作用在fcc晶体的[001]方向上,求作用在(111)
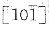
和(111)
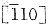
滑移系上的分切应力。
矢量数性积:
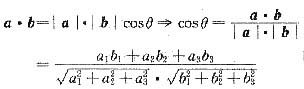
(111)
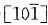
滑移系:
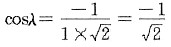
(负号不影响切应力大小,故取正号)
(111)
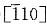
滑移系:
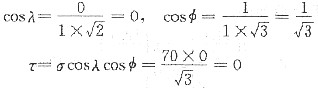
10. 有一bcc晶体的
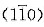
[111]滑移系的临界分切力为60MPa,试问在[001]和[010]方向必须施加多少的应力才会产生滑移?
矢量数性积:
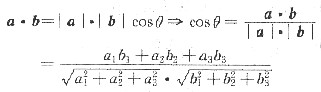
[001]方向:
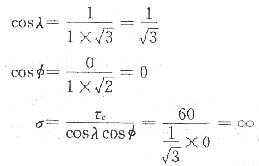
故在此方向上无论施加多大应力都不能产生滑移。
[010]方向:

11. Zn单晶在拉伸之前的滑移方向与拉伸轴的夹角为45°,拉伸后滑移方向与拉伸轴的夹角为30°,求拉伸后的延伸率。
如图26所示,AC和A'C'分别为拉伸前后晶体中两相邻滑移面之间的距离。因为拉伸前后滑移面间距不变,即AC=A'C',故
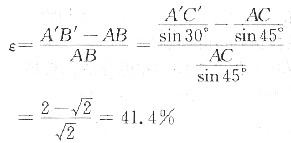
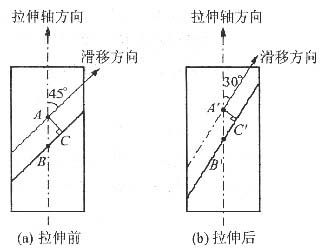
12. Al单晶在室温时的临界分切应力τ
c=7.9×10
5Pa。若在室温下将铝单晶试样做拉伸试验时,拉伸轴为[123]方向,试计算引起该样品屈服所需施加的应力。
Al系fcc晶体结构,其滑移系为{111}<110>。
当外力轴为[123]时,根据映像规则从立方晶系的标准投影图得知,首先开动的滑移系为
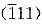
[101],故φ为[123]与
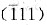
晶面的法线
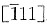
之间的夹角,λ为[123]与[101]之间的夹角,
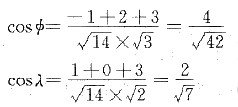
故
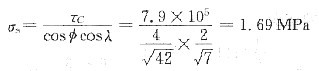
13. 将Al单晶制成拉伸试棒(其截面积为9mm
2)进行室温拉伸,拉伸轴与[001]相交成36.7°,与[011]相交成19.1°,与[111]相交成22.2°,开始屈服时载荷为20.4N,试确定主滑移系的分切应力。
由已知的拉伸轴方向,根据立方晶系(001)标准投影图可以确定主滑移系为
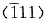
[101]。设应力轴方向为[uvw],从已知条件有
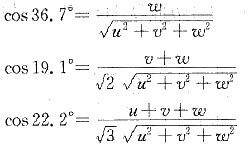
令u
2+v
2+w
2=1,可解得u=0.26,v=0.54,w=0.80
所以
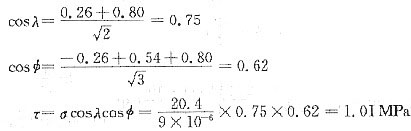
14. Mg单晶体的试样拉伸时,3个滑移方向与拉伸轴分别相交成38°,45°,85°,而基面法线与拉伸轴相交成60°。如果在拉应力为2.05MPa时开始观察到塑性变形,则Mg的临界分切应力为多少?
Mg的滑移面为(0001)面(基面),由滑移面的滑移方向上的分切应力τ=σcosλcosφ可知,当φ为定值(60°)时,λ越小,τ越大,所以在拉应力作用下,晶体沿与拉伸轴交成38°的那个滑移方向滑移而产生塑性变形。因此Mg的临界分切应力
τc=σscosλcosφ=2.05×cos60°×cos38°
=2.05×0.5×0.788=0.8077MPa
15. MgO为NaCl型结构,其滑移面为{110},滑移方向为<110>,试问沿哪一方向拉伸(或压缩)不会引起滑移?
根据氧化镁结构滑移系的特点,只有沿与所有<110>都垂直的方向拉伸(或压缩)才不会引起滑移。
由立方晶系(001)标准投影图可知,不可能存在与所有<110>极点都相距90°的极点,因此,对氧化镁不存在任何不会引起滑移的拉伸(或压缩)方向。
16. 一个交滑移系包含一个滑移方向和包含这个滑移方向的两个晶面,如bcc晶体的(101)
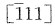
(110),写出bcc晶体的其他3个同类型的交滑移系。
由立方晶系(001)标准投影图可查得,bcc晶体其他3个同类型的交滑移系是:
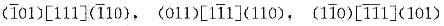
17. fcc和bcc金属在塑性变形时,流变应力与位错密度ρ的关系为
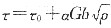
,式中τ
0为没有干扰位错时使位错运动所需的应力,也即无加工硬化时所需的切应力,G为切变模量,b为位错的伯氏矢量,α为与材料有关的常数,α=0.3~0.5。实际上,此公式也是加工硬化方法的强化效果的定量关系式。若Cu单晶体的τ
0=700kPa,初始位错密度ρ
0=10
5cm
-2,则临界分切应力为多少?已知Cu的G=42×10
3MPa,b=0.256nm,[111]eu单晶产生1%塑性变形所对应的σ=40MPa,求它产生1%塑性变形后的位错密度。
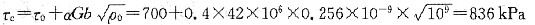
由立方晶系(001)标准投影图查得拉伸轴为[111]时,可开动的滑移系为
[011]及另外5个与其等效的滑移系,可算得开动其中任一滑移系时取向因子都为
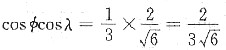
故
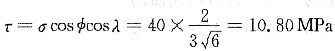
由
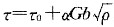
,可算得:

18. 证明:bcc及fcc金属产生孪品时,孪晶面沿孪生方向的切变均为0.707。
bcc晶体的孪晶面为{112},孪生方向为<111>,孪生时切过距离为
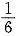
<111>,故孪生时孪晶面沿孪生方向的切变
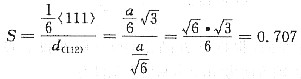
fcc晶体的孪晶面为{111},孪生方向为<112>,孪生时切过距离为
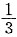
<112>,故孪生时孪晶面沿孪生方向的切变
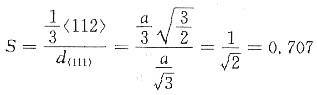
19. 试指出Cu和α-Fe两晶体易滑移的晶面和晶向,并求出他们的滑移面间距,滑移方向上的原子间及点阵阻力。(已知G
Cu=48.3GPa,G
α-Fe=81.6GPa,υ=0.3)。
Cu系fcc结构,其易滑移面为{111},易滑移方向为<110>。
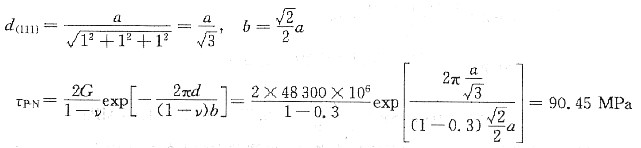
α-Fe系bcc结构,其滑移面为{110},易滑移方向为(111)。
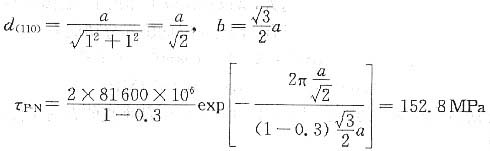
20. 设运动位错被钉扎以后,其平均间距
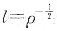
(ρ为位错密度),又设Cu单晶已经应变硬化到这种程度,作用在该晶体所产生的分切应力为14MPa,已知G=40GPa,b=0.256nm,计算Cu单晶的位错密度。
运动位错被钉扎以后,长度为l的位错线段可作为位错源,所产生的分切应力即为开动此位错源所需的分切应力,即
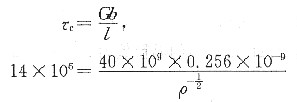
故
ρ=1.869×10
12m
-2
21. 设合金中一段直位错线运动时受到间距为λ的第二相粒子的阻碍,试求证:使位错按绕过机制继续运动所需的切应力为:
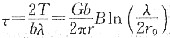
,式中,T为线张力;b为伯氏矢量;G为切变模量;r
0为第二相粒子半径;B为常数。
不可变形粒子的强化作用:
运动的位错与不可变形粒子相遇时,将受其阻挡,使位错线绕着它发生弯曲。由于位错具有线张力T,故要使位错线弯曲,必须克服其线张力的作用。位错线绕过间距为λ的粒子时,所需切应力

位错的线张力相似于液体的表面张力,可用单位长度位错的能量来表示,而单位长度位错的能量
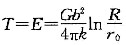
,代入上式,则
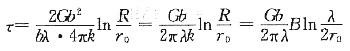
其中
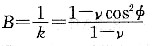
22. 40钢经球化退火后,渗碳体全部呈半径为10μm的球状,且均匀地分布在α-Fe基础上。已知Fe的切变模量G=7.9×10
4MPa,α-Fe的点阵常数a=0.28nm,试计算40钢的切变强度。
为了方便起见,计算时忽略基体相α-Fe中的ω
C,并忽略Fe与Fe
3C密度上的差异。对40钢,碳的质量分数ω
C=0.004,则Fe
3C相所占体积分数
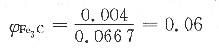
若单位体积内Fe
3C的颗粒数为N
V,则
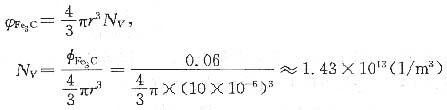
故
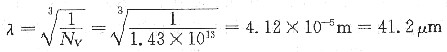
第二相硬质点的弥散强化效果决定于第二相的分散度,故
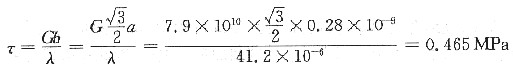
23. 已知平均晶粒直径为1mm和0.0625mm的α-Fe的屈服强度分别为112.7MPa和196MPa,问平均晶粒直径为0.0196mm的纯铁的屈服强度为多少?
24. 已知工业纯铜的屈服强度σ
S=70MPa,其晶粒大小为N
A=18个/mm
2,当N
A=4025个/mm
2时,σ
S=95MPa。试计算N
A=260个/mm
2时的σ
S。
设晶粒的平均直径为d,每mm
2内的晶粒数为N
A,可以证明:
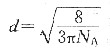
故

代入Hall-Petch公式,即

解得
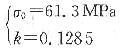
故
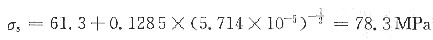
25. 简述陶瓷材料(晶态)塑性变形的特点。
总的来说,相对于金属材料和高分子材料而言,陶瓷材料显得硬而脆,这是由其原子之间键合的类型所决定的。陶瓷材料原子之间通常是由离子键、共价键所构成的。在共价键合的陶瓷中,原子之间是通过共用电子对形式进行键合的,具有方向性和饱和性,并且其键能相当高。在塑性变形时,位错的运动势必会破坏原子间的共价键合,其点阵阻力(P-N力)很大。因此,共价键合的陶瓷表现为硬而脆的特性。而对离子键合的陶瓷材料则分为两种情况:单晶体(如NaCl,FeO等)在室温压应力作用下,可承受较大的塑性变形,然而,对于离子键的多晶陶瓷,往往很脆,且易在晶界形成裂纹,这是因为离子晶体要求正负离子相间排列。在外力作用下,当位错运动一个原子间距时,由于存在巨大的同号离子的库仑静电斥力,致使位错沿垂直或平行于离子键方向很难运动。但若位错沿45°方向而不是沿水平方向运动,则在滑移过程中,相邻晶面始终由库仑力保持相吸,因此具有相当好的塑性。然而,多晶体陶瓷变形时,要求相邻晶粒变形相互协调、相互制约,由于陶瓷的滑移系较少而难以实现,以至在晶界产生开裂现象,最终导致脆断。
另一方面,烧结合成的陶瓷材料在加热冷却过程中,由于热应力的存在,往往导致显微裂纹的产生;由于腐蚀等因素也会在其表面形成裂纹,因此在陶瓷材料中先天性裂纹或多或少地总是存在。在外力作用下,在裂纹尖端会产生严重的应力集中。按照弹性力学估算,裂纹尖端的最大应力可达到理论断裂强度;何况陶瓷晶体中可动位错少,位错运动又困难,故一旦达到屈服强度往往就脆断了。当然,在拉伸或压缩的情况下,陶瓷材料的力学特性也有明显的不同,通常陶瓷的压缩强度总是高于抗拉强度。
26. 脆性材料的抗拉强度可用下式表示:
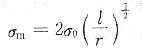
式中,σ
0为名义上所施加的拉应力;l为表面裂纹的长度或者为内部裂纹长度的
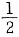
;r为裂纹尖端的曲率半径;σ
m实际上为裂纹尖端处应力集中导致的最大应力。现假定Al
2O
3陶瓷的表面裂纹的临界长度为l=2×10
-3mm,其理论的断裂强度为
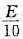
(E为材料的弹性模量),且为393GPa,试计算:当Al
2O
3陶瓷试样施加上275MPa拉应力时,产生断裂的裂纹尖端临界曲率半径r
c。
当拉应力σ
m达到材料的断裂强度
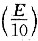
时,Al
2O
3断裂,因此
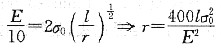
故
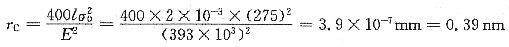
27. 三点弯曲试验常用来检测陶瓷材料的力学行为。有一圆形截面的Al
2O
3试样,其截面半径r=3.5mm,两支点间距为50mm,当负荷达到950N时,试样断裂。试问:当支点间距为40mm时,另一个具有边长为12mm正方形截面的同样材料试样在多大负荷时会发生断裂?
当采用三点弯曲法检测时,对矩形断面样品,其断裂强度
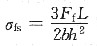
式中F
f为断裂时负荷;L为支点间距离;b为截面宽度;h为截面高度。对于圆形截面样品,则其断裂强度
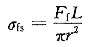
式中r为试样截面半径。
将已知条件代入相关公式,得

故
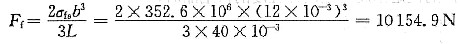
28. 对于许多高分子材料,其抗拉强度σ
b是数均相对分子质量
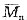
的函数:
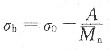
式中,σ
0为无限大分子量时的抗拉强度;A为常数。已知两种聚甲基丙烯酸甲酯的数均相对分子质量分别为4×10
4和6×10
4,所对应的抗拉强度则分别为107MPa和170MPa,试确定数均相对分子质量为3×10
4时的抗拉强度σ
b。
29. 解释高聚物在单向拉伸过程中细颈截面积保持基本不变的现象。
很多高聚物在塑性变形时往往会出现均匀变形的不稳定性。如将某一高聚物样品进行单向拉伸试验,开始时应力随应变线性增加,试样被均匀地拉长,过了屈服点后,在试样某个部位的应变突然比整体应变增加得更快,使原来均匀的截面变得不均匀,出现一个或几个细颈。继续变形时,颈缩区不断扩展,沿着试样长度方向不断延伸,直到整个试样的截面都均匀变细为止,在这一变形过程中应力几乎不变。如《材料科学基础》第221页中图5.83所示。这是因为超过屈服强度后,试样产生塑性变形,并在颈缩处出现了加工硬化。XRD分析证明,高聚物中的大分子无论是非晶态还是结晶态,随着变形程度的增加,都逐渐发生沿外力方向的定向排列。由于键(主要是共价键)的方向性,在产生定向排列后发生了应变硬化。
30. 现有一φ6mm铝丝须最终加工至φ0.5mm铝材,但为保证产品质量,此铝材的冷加工量不能超过85%,如何制订其合理的加工工艺?

故
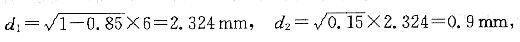
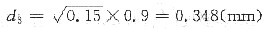
因此,可先将φ6mm的铝丝冷拔至φ2.324mm,接着进行再结晶退火,以消除加工硬化,然后冷拔至φ0.9mm,再进行再结晶退火,最终冷拔至φ0.5mm即可。
31. 铁的回复激活能为88.9kJ/mol,如果将经冷变形的铁在400℃下进行回复处理,使其残留加工硬化为60%需160min,问在450℃下回复处理至同样效果需要多少时间?
32. Ag冷加工后位错密度为10
12/cm
2,设再结晶晶核自大角度晶界向变形基体移动,求晶界弓出的最小曲率半径(Ag:G=30GPa,b=0.3nm,γ=0.4J/m
2)。
Ag再结晶晶核自大角度晶界向变形基体移动的驱动力F为冷加工存储能,F=Gb
2(ρ
1-ρ
0),由于ρ
1>>ρ
0,故F≈Gb
2ρ
1。
弓出后的晶界会受到指向其曲率中心的力厂作用,当弓出的曲率半径为R时,f=
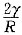
,f与F反向,晶界弓出的最小曲率半径R
min应为f与F平衡时的半径,
F=f

33. 已知纯铁经冷轧后,在527℃加热产生50%的再结晶所需的时间为10
4s,而在727℃加热产生50%再结晶所需的时间仅为0.1s,试计算在10
5s时间内产生50%的再结晶的最低温度为多少摄氏度?
在两个不同的恒定温度产生同样程度的再结晶时,
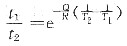
或
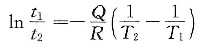
故

34. 假定将再结晶温度定义为退火1h内完成转变量达95%的温度,已知获得95%转变量所需要的时间:
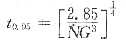
式中,N,G分别为再结晶的形核率和长大线速度,
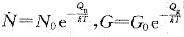
。
①根据上述方程导出再结晶温度T
R与G
0,N
0,Q
R及Q
n的函数关系。
②说明下列因素是怎样影响G
0,N
0,Q
R及Q
n的:
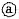
预变形度;

原始晶粒度;

金属纯度。
③说明上述3个因素是怎样影响再结晶温度的。
①
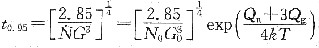
将T=T
R,t
0.95=1代入,得

故
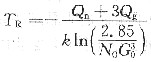
②一次再结晶的驱动力是晶体经变形后的畸变能。晶体从畸变后的高能态向退火状态的低能态转变是一自发趋势。但这一能态的变化要求原子越过一势垒△E,势垒的高度取决于变形后的晶格畸变能,当畸变能高时,△E减小,则形核和长大激活能Q
n,Q
g均降低,再结晶速度便加快。因此,一切影响变形后畸变能的因素均会影响Q
n,Q
g及T
R。
由上述分析,在一定形变度范围内,预先变形程度越高,原始晶粒越细,则形变后畸变能越大,Q
n,Q
g越低。 金属的纯度对Q
n,Q
g的影响可以从两方面考虑,一方面杂质会增加畸变能,使Q
n,Q
g降低;另一方面,杂质也会阻碍界面迁移,使Q
n,Q
g增高;两个相反的作用同时存在,看何者占主导地位。N
0G
0只与金属的本性有关,预变形度、原始晶粒尺寸和金属纯度对其无多大影响。
③由②的分析可知,增大预变形度,细化原始晶粒,将使T
R下降。
杂质对T
R的影响具有双重性,若杂质的存在使畸变能增大这一因素占主导地位,则纯度较低的金属,其T
R较低;反之,若杂质的存在使界面迁移减慢这一因素占主导地位,则纯度越高的金属,其T
R越低。不同的杂质原子对T
R的影响不同,一般来说,少量杂质原子的存在会阻碍金属的再结晶,从而使T
R上升,其提高的程度因杂质种类不同而异。
35. 已知Fe的T
m=1538℃,Cu的T
m=1083℃,试估算Fe和Cu的最低再结晶温度。
根据经验公式,再结晶温度T再≈0.4Tm
故Fe的最低再结晶温度T再=0.4×(1538+273)=724.4K=451.4℃
Cu的最低再结晶温度T再=0.4×(1083+273)=542.4K=269.4℃
生产中为了提高生产效率,工厂中实际再结晶退火温度通常选定为T再+(1.0~200)℃。
36. 工业纯铝在室温下经大变形量轧制成带材后,测得室温力学性能为冷加工态的性能。查表得知:工业纯铝的再结晶温度T
再=150℃,但若将上述工业纯铝薄带加热至100℃,保温16d后冷至室温再测其强度,发现强度明显降低,请解释其原因。
查表所得工业纯铝的再结晶温度T
再=150℃是指在1h退火完成再结晶的温度。实际上,除了退火温度外,保温时间也对再结晶过程产生影响。对经大冷变形后的金属材料,即使在T<T
再时进行退火,只要保温时间足够,同样可发生再结晶过程。可用两种方法加以判断:①金相检验;②将已知的T
1,t
1,t
2,Q代入公式
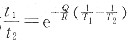
,求得T
2,将其与100℃比较,即可得知是否发生再结晶。
37. 某工厂用一冷拉钢丝绳将一大型钢件吊人热处理炉内,由于一时疏忽,未将钢丝绳取出,而是随同工件一起加热至860℃,保温时间到了,打开炉门,要吊出工件时,钢丝绳发生断裂,试分析原因。
冷拉钢丝绳系经大变形量的冷拔钢丝绞合而成。加工过程的冷加工硬化使钢丝的强度、硬度大大提高,从而能承载很重的工件。但是当将其加热至860℃时,其温度已远远超过钢丝绳的再结晶温度,以致产生回复再结晶现象,加工硬化效果完全消失,强度、硬度大大降低。再把它用来起重时,一旦负载超过其承载能力,必然导致钢丝绳断裂事故。
38. 已知H70黄铜[ω(Zn)=30%]在400℃的恒温下完成再结晶需要1h,而在390℃下完成再结晶需要2h,试计算在420℃恒温下完成再结晶需要多少时间?
再结晶是一热激活过程,再结晶速率
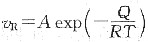
,它与产生某一体积分数所需的时间t成反比,即
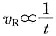
,故
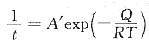
在两个不同的恒定温度产生同样程度的再结晶时,
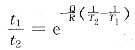
两边取对数得
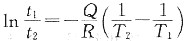
;同样
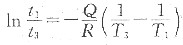
故得
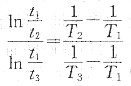
代入相应的数据,得到
t
3=0.26h
39. 设有1cm
3黄铜,在700℃退火,原始晶粒直径为2.16×10
-3cm,黄铜的界面能为0.5J/m
2,由量热计测得保温2h共放出热量0.035J,求保温2h后的晶粒尺寸。
设保温2h放出的热量是由于晶粒长大、晶界总面积减小而释放的能量,而从定量金相得知,单位体积界面面积S
V和截面上晶粒直径d之间有
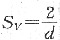
的关系,因此,
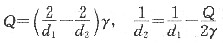
代入相应的数据,得
d
2=8.9×10
-3cm
40. 设冷变形后位错密度为10
12/cm
2的金属中,存在着加热时不发生聚集长大的第二相微粒,其体积分数φ=1%,半径为1μm,问这种第二相微粒的存在能否完全阻止此金属加热时再结晶(已知G=10
5MPa,b=0.3nm,比界面能σ=0.5J/m
2)。
再结晶驱动力
F=Gb
2(ρ-ρ
0)≈Gb
2ρ=10
11×(3×10
-10)
2×10
16=9×10
7N/m
2 再结晶阻力
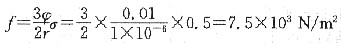
F>>f,故这种第二相微粒的存在不能完全阻止再结晶。
41. W具有很高的熔点(T
m=3410℃),常被选为白炽灯泡的发热体。但当灯丝存在横跨灯丝的大晶粒时就会变得很脆,并在频繁开关的热冲击下产生破断。试介绍一种能延长灯丝寿命的方法。
影响再结晶晶粒正常长大的因素,除了温度外,弥散分布的第二相粒子的存在,对晶界迁移也起着重要作用。例如,可在钨丝中形成弥散分布的ThO
2第二相质点,以阻碍灯丝在高温工作过程中晶粒长大。若ThO
2质点的体积分数为φ,质点半径为r时,则晶粒的极限尺寸为:
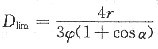
式中α为接触角。因此,选择合适的φ和r,可使D
lim尽可能小,而且晶粒细化可提高其强度,同时保持较高水平的韧性,从而有效地延长灯丝的使用寿命。
42. Fe-3%Si合金含有MnS粒子时,若其半径为0.05μm,体积分数为0.01,在850℃以下退火过程中,当基体晶粒平均直径为6μm时,其正常长大即行停止,试分析其原因。
对含有半径为0.05μm,体积分数为0.01的MnS粒子的矽钢片再结晶时,其极限晶粒的平均直径
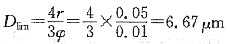
正因为有这种分散相粒子的存在,从而使矽钢片在850℃以下退火时,当基体晶粒平均直径为6μm时,其正常长大即行停止。
43. 工程上,常常认为钢加热至760℃时晶粒并不长大,而在870℃时晶粒将明显长大。若钢的原始晶粒直径为0.05mm,晶粒长大经验公式为
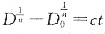
,其中:D为长大后的晶粒直径;D
0为原始晶粒直径;c为比例常数;t为保温时间。
已知760℃时,n=0.1,c=6×10
-16;870℃时,n=0.2,c=2×10
-8,求叫(C)为0.8%的钢在上述两温度下保温1h的晶粒直径。
760℃时:
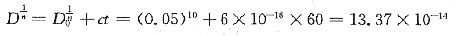
D=0.0516mm
故此晶粒基本上未长大;
870℃时:D
5=(0.05)
5+2×10
-8×60=1.513×10
-6 D=0.0686mm
相对的原始晶粒直径已明显长大(约37%)。
44. 简述一次再结晶与二次再结晶的驱动力,并如何区分冷、热加工?动态再结晶与静态再结晶后的组织结构的主要区别是什么?
一次再结晶的驱动力是基体的弹性畸变能,而二次再结晶的驱动力是来自界面能的降低。再结晶温度是区分冷、热加工的分界线。动态再结晶后的组织结构虽然也是等轴晶粒,但晶界呈锯齿状,晶粒内还包含着被位错缠结所分割的亚晶粒,这与静态再结晶后所产生的位错密度很低的晶粒不同,故同样晶粒大小的动态再结晶组织的强度和硬度要比静态再结晶的高。动态再结晶后的晶粒大小与流变应力成正比。此外,应变速率越低,形变温度越高,则动态再结晶后的晶粒越大,而且越完整。
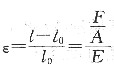 ,所以
,所以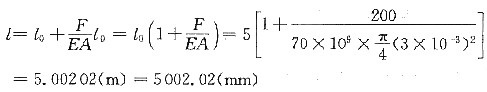
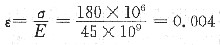
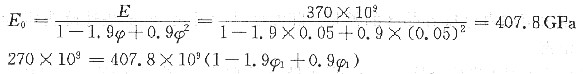
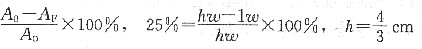
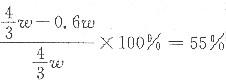
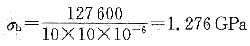
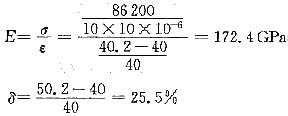
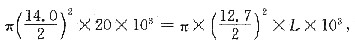
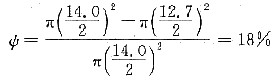
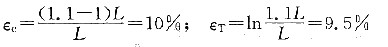

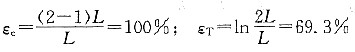
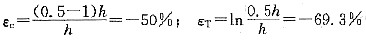
 ,二者真实应变量的绝对值相等,而工程应变量的绝对值却不相等,所以用真实应变更能反映真实的变形特性。
,二者真实应变量的绝对值相等,而工程应变量的绝对值却不相等,所以用真实应变更能反映真实的变形特性。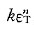 ,其中k和n为经验常数,分别称为强度系数和应变硬化指数。若有A,B两种材料,其走值大致相等,而nA=0.5,nB=0.2,则问:①哪一种材料的硬化能力较高,为什么?②同样的塑性应变时,A和B哪个位错密度高,为什么?③导出应变硬化指数n和应变硬化率
,其中k和n为经验常数,分别称为强度系数和应变硬化指数。若有A,B两种材料,其走值大致相等,而nA=0.5,nB=0.2,则问:①哪一种材料的硬化能力较高,为什么?②同样的塑性应变时,A和B哪个位错密度高,为什么?③导出应变硬化指数n和应变硬化率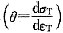 之间的数学公式。
之间的数学公式。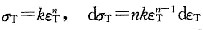 ,所以
,所以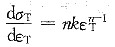
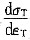 也较大,所以A比B的应变硬化能力高。
也较大,所以A比B的应变硬化能力高。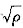 ,所以n越大,ρ越小,由于A的n值比B的高,所以在同样的塑性应变时,B的位错密度高。
,所以n越大,ρ越小,由于A的n值比B的高,所以在同样的塑性应变时,B的位错密度高。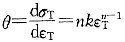 ,将
,将 代入,得
代入,得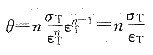
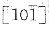 和(111)
和(111)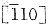 滑移系上的分切应力。
滑移系上的分切应力。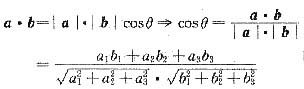
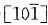 滑移系:
滑移系: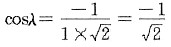 (负号不影响切应力大小,故取正号)
(负号不影响切应力大小,故取正号)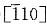 滑移系:
滑移系: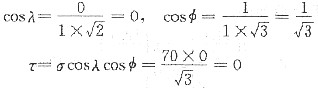
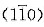 [111]滑移系的临界分切力为60MPa,试问在[001]和[010]方向必须施加多少的应力才会产生滑移?
[111]滑移系的临界分切力为60MPa,试问在[001]和[010]方向必须施加多少的应力才会产生滑移?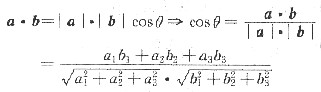
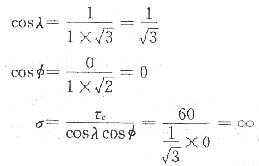

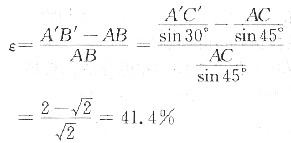

 [101],故φ为[123]与
[101],故φ为[123]与 晶面的法线
晶面的法线 之间的夹角,λ为[123]与[101]之间的夹角,
之间的夹角,λ为[123]与[101]之间的夹角,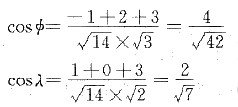
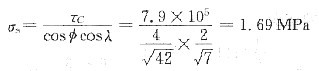
 [101]。设应力轴方向为[uvw],从已知条件有
[101]。设应力轴方向为[uvw],从已知条件有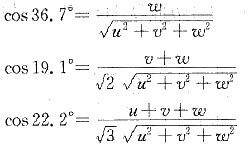
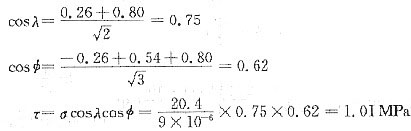
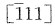 (110),写出bcc晶体的其他3个同类型的交滑移系。
(110),写出bcc晶体的其他3个同类型的交滑移系。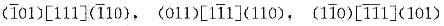
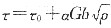 ,式中τ0为没有干扰位错时使位错运动所需的应力,也即无加工硬化时所需的切应力,G为切变模量,b为位错的伯氏矢量,α为与材料有关的常数,α=0.3~0.5。实际上,此公式也是加工硬化方法的强化效果的定量关系式。若Cu单晶体的τ0=700kPa,初始位错密度ρ0=105cm-2,则临界分切应力为多少?已知Cu的G=42×103MPa,b=0.256nm,[111]eu单晶产生1%塑性变形所对应的σ=40MPa,求它产生1%塑性变形后的位错密度。
,式中τ0为没有干扰位错时使位错运动所需的应力,也即无加工硬化时所需的切应力,G为切变模量,b为位错的伯氏矢量,α为与材料有关的常数,α=0.3~0.5。实际上,此公式也是加工硬化方法的强化效果的定量关系式。若Cu单晶体的τ0=700kPa,初始位错密度ρ0=105cm-2,则临界分切应力为多少?已知Cu的G=42×103MPa,b=0.256nm,[111]eu单晶产生1%塑性变形所对应的σ=40MPa,求它产生1%塑性变形后的位错密度。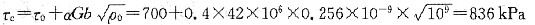
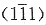 [011]及另外5个与其等效的滑移系,可算得开动其中任一滑移系时取向因子都为
[011]及另外5个与其等效的滑移系,可算得开动其中任一滑移系时取向因子都为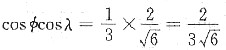
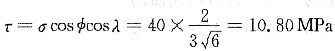
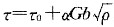 ,可算得:
,可算得:
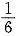 <111>,故孪生时孪晶面沿孪生方向的切变
<111>,故孪生时孪晶面沿孪生方向的切变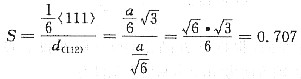
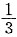 <112>,故孪生时孪晶面沿孪生方向的切变
<112>,故孪生时孪晶面沿孪生方向的切变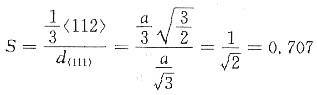
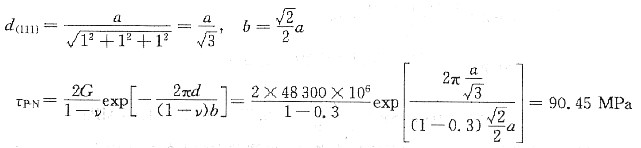
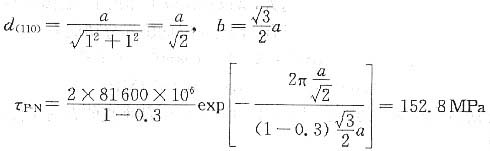
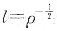 (ρ为位错密度),又设Cu单晶已经应变硬化到这种程度,作用在该晶体所产生的分切应力为14MPa,已知G=40GPa,b=0.256nm,计算Cu单晶的位错密度。
(ρ为位错密度),又设Cu单晶已经应变硬化到这种程度,作用在该晶体所产生的分切应力为14MPa,已知G=40GPa,b=0.256nm,计算Cu单晶的位错密度。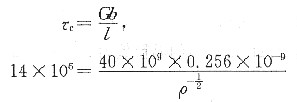
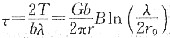 ,式中,T为线张力;b为伯氏矢量;G为切变模量;r0为第二相粒子半径;B为常数。
,式中,T为线张力;b为伯氏矢量;G为切变模量;r0为第二相粒子半径;B为常数。
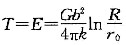 ,代入上式,则
,代入上式,则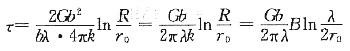
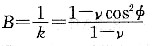
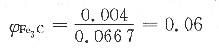
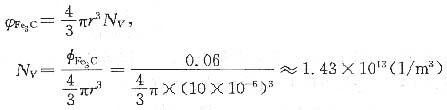
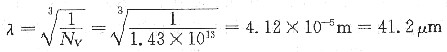
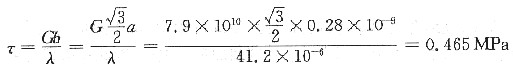
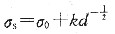


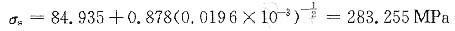
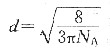


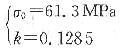
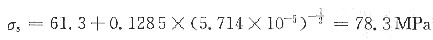
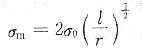
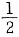 ;r为裂纹尖端的曲率半径;σm实际上为裂纹尖端处应力集中导致的最大应力。现假定Al2O3陶瓷的表面裂纹的临界长度为l=2×10-3mm,其理论的断裂强度为
;r为裂纹尖端的曲率半径;σm实际上为裂纹尖端处应力集中导致的最大应力。现假定Al2O3陶瓷的表面裂纹的临界长度为l=2×10-3mm,其理论的断裂强度为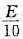 (E为材料的弹性模量),且为393GPa,试计算:当Al2O3陶瓷试样施加上275MPa拉应力时,产生断裂的裂纹尖端临界曲率半径rc。
(E为材料的弹性模量),且为393GPa,试计算:当Al2O3陶瓷试样施加上275MPa拉应力时,产生断裂的裂纹尖端临界曲率半径rc。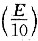 时,Al2O3断裂,因此
时,Al2O3断裂,因此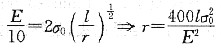
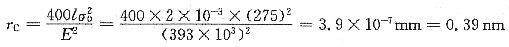
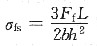
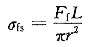

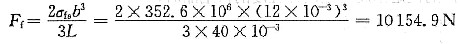
 的函数:
的函数: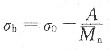
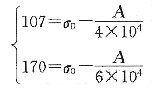
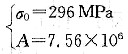
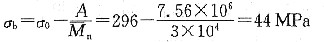

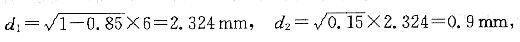
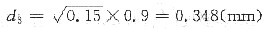
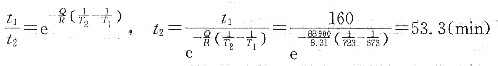
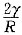 ,f与F反向,晶界弓出的最小曲率半径Rmin应为f与F平衡时的半径,
,f与F反向,晶界弓出的最小曲率半径Rmin应为f与F平衡时的半径,
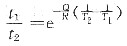
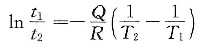

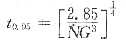
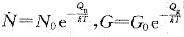 。
。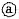 预变形度;
预变形度; 原始晶粒度;
原始晶粒度; 金属纯度。
金属纯度。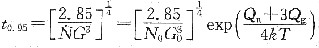

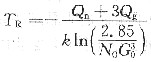
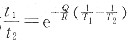 ,求得T2,将其与100℃比较,即可得知是否发生再结晶。
,求得T2,将其与100℃比较,即可得知是否发生再结晶。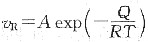 ,它与产生某一体积分数所需的时间t成反比,即
,它与产生某一体积分数所需的时间t成反比,即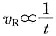 ,故
,故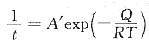
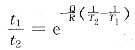
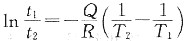 ;同样
;同样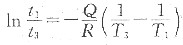
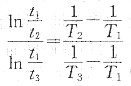
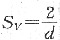 的关系,因此,
的关系,因此,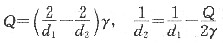
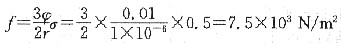
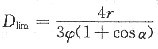
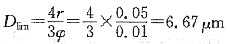
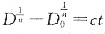 ,其中:D为长大后的晶粒直径;D0为原始晶粒直径;c为比例常数;t为保温时间。
,其中:D为长大后的晶粒直径;D0为原始晶粒直径;c为比例常数;t为保温时间。