银符考试题库B12
现在是:
试卷总分:100.0
您的得分:
考试时间为:
点击“开始答卷”进行答题
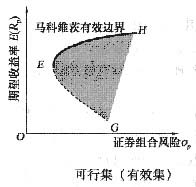
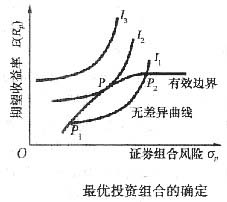
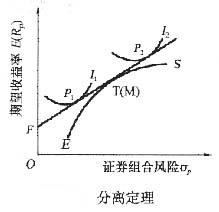
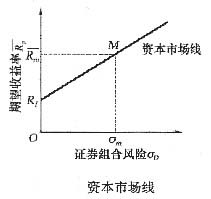
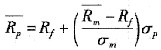 (5-1)
(5-1)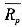 表示最优投资组合的预期收益率;Rf表示无风险利率;
表示最优投资组合的预期收益率;Rf表示无风险利率;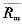 表示市场组合预期收益率;σm表示市场组合的标准差;σp表示最优投资组合的标准差。
表示市场组合预期收益率;σm表示市场组合的标准差;σp表示最优投资组合的标准差。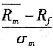 ,它们分别代表时间报酬和风险报酬。因此,从本质上说,证券市场提供了时间和风险进行交易的场所,其价格则由供求双方的力量来决定。资本市场线的实质就是在允许无风险借贷情况下的有效集。它反映了当市场达到均衡时,市场组合与无风险资产所形成的有效组合的收益与风险的关系。
,它们分别代表时间报酬和风险报酬。因此,从本质上说,证券市场提供了时间和风险进行交易的场所,其价格则由供求双方的力量来决定。资本市场线的实质就是在允许无风险借贷情况下的有效集。它反映了当市场达到均衡时,市场组合与无风险资产所形成的有效组合的收益与风险的关系。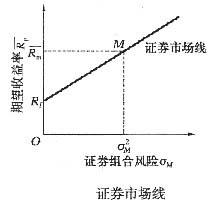
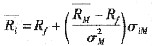 (5-2)
(5-2)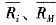 和Rf分别表示单个证券的预期收益率、市场组合预期收益率和无风险利率;
和Rf分别表示单个证券的预期收益率、市场组合预期收益率和无风险利率;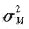 表示市场组合的方差(风险);σim表示证券i与市场组合的协方差。
表示市场组合的方差(风险);σim表示证券i与市场组合的协方差。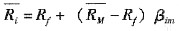 (5-3)
(5-3)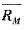 ,因此其坐标为(1,
,因此其坐标为(1,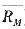 )。在无风险资产那一点,β值为0,预期收益率为Rf,因此其坐标为(0,Rf)。
)。在无风险资产那一点,β值为0,预期收益率为Rf,因此其坐标为(0,Rf)。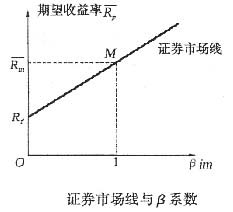
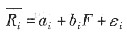 (5-4)
(5-4)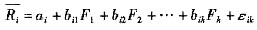 (5-5)
(5-5) (5-6)
(5-6)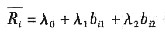 (5-7)
(5-7)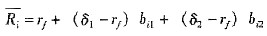 (5-8)
(5-8)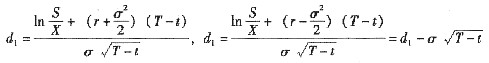
 半强势信息集
半强势信息集 强势信息集
强势信息集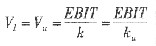 (5-10)
(5-10)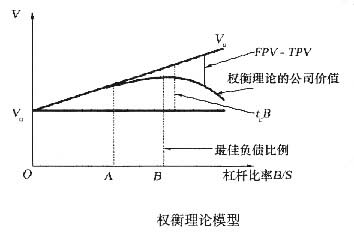
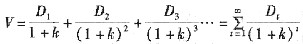 (5-13)
(5-13)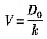 (5-14)
(5-14)

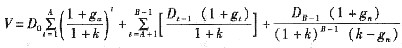 (5-15)
(5-15)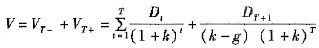 (5-16)
(5-16)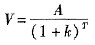 (5-17)
(5-17)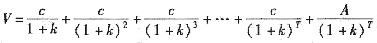 (5-18)
(5-18)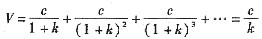 (5-19)
(5-19)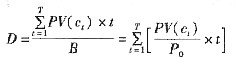 (5-20)
(5-20)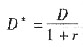
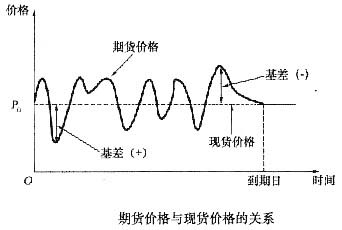
表5-1 债券属性与债券收益率
|
