一、单项选择题2. 已知函数f(x,y)在(0,1)处的偏导数存在,则
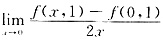
A.f
x(0,1) B.f
x(0,2)
C.
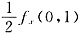
D.2f
x(0,1)
A B C D
C
[解析] 本题考查偏导数.
[要点透析]
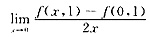
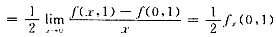
3. n为半球x
2+y
2+z
2≤1,z≥0,则三重积分
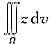

A B C D
D
[解析] 本题考查球面坐标下的三重积分.
[要点透析] 由球面坐标下三重积分的计算公式可得
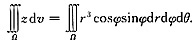
由Ω为半球x
2+y
2+z
2≤1,x≥0可知,0≤r≤1,
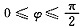
,0≤θ≤2π
于是
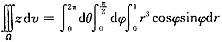
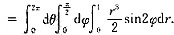
二、填空题1. 微分方程
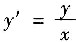
满足初始条件y(1)=1的特解是______.
y=x
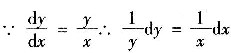
两端积分得lny=lnx+lnC∴通解为y=cx,把x=1,y=1代入得
c=1,故特解为y=x
2. 三重积分
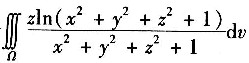
=______,其中Ω是球x
2+y
2+z
2≤1.
0
因为Ω关于平面z对称,
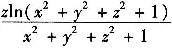
为z的奇函数
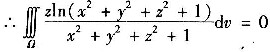
3. 极限
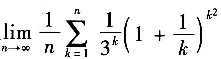
=______.
0
考虑级数
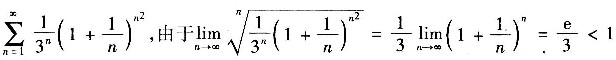
所以,这一正项级数收敛,因此
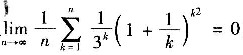
4. 微分方程y"+4y'+3y=0的通解为y=______.
c1e-x+c2e-3x
∵特征方程为r2+4r+3=0∴r1=-3,r2=-1,从而通解为y=c1e-x+c2e-3x
5. 设f(x)是周期为2π的周期函数,它在[-π,π]上表达式为
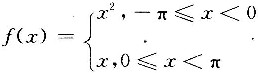
,s(x)是f(x)的傅里叶级数的和函数,则s(π)=______.
三、计算题1. 计算二重积分
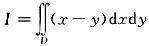
,其中D是由x+y=-1,x=0,y=0所围成的区域.
积分区域D,如下图所示,于是
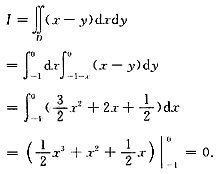
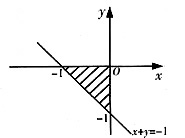
[考点点击] 主要考查的知识点为二重积分的计算.
3. 求过点A
0,1,1),B1,2,0)与x轴平行的平面方程.
设所求平面的法向量为n,则
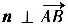
又
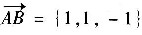
,在x轴上取单位向量i={1,0,0},则n⊥i,取
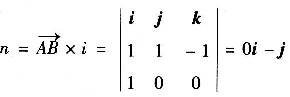
-k,故所求平面方程为(-1)(y-1)+(-1)(z-1)=0,即y+z-2=0
4. 判断无穷级数
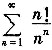
的敛散性.
由正项级数比值审敛法
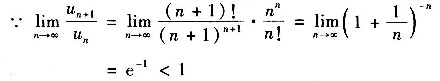
∴原级数收敛
5. 求过点P(-1,2,-3),并且与直线x=3+t,y=t,z=1-t垂直的平面方程.
解:∵平面的法向量为{1,1,-1}
∴所求平面方程为1·(x+1)+1·(y-2)+(-1)(z+3)=0
即x+y-z-4=0.
6. 设函数z=ln(x
2+y
2)-sinxy,求全微分dz.
7. 设函数
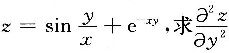
.
8. 求函数f(x,y)=x
2+xy+y
2+x-y+2的极值.
∵F(x,y) =x
2+xy+y
2+x-y+2 令
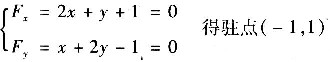
A=F
xx(-1,1)=2,B=F
xy(-1,1)=1,C=F
yy(-1,1)=2
∴B=AC=-3<0又A=2>0 ∴f(x,y)在(-1,1)处取得极小值.
极小值为f(-1,1)=1
9. 设由方程
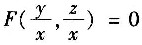
确立的隐函数z=f(x,y),其中F具有连续的一阶偏导数,求
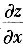
,
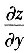
.
用隐函数求偏导公式
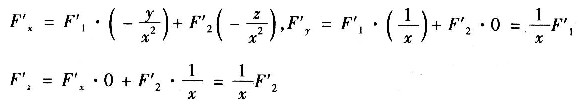
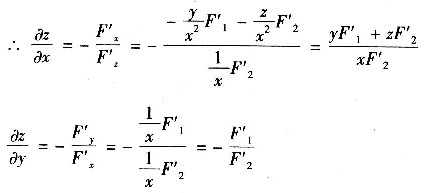
10. 已知a={1,1,-4},b={1,-2,2},求(1)a·b;(2)a与b的夹角;(3)a在b上的投影ab.
(1)a·b=1×1+1×(-2)+(-4)×2=-9
(2)设夹角为φ,那么
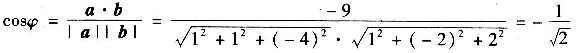
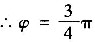
(3)a·b=|a|·|b|cosφ=|b|a
b ∴a在b上的投影为
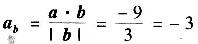
11. 设L为折线OAB,其中O(0,0),A(1,1),B(1,0),求曲线积分
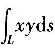
.
12. 计算二重积分
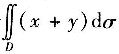
,其中D为y=x
2,y=4x
2及y=1所围成的闭区域.
积分区域如图所示
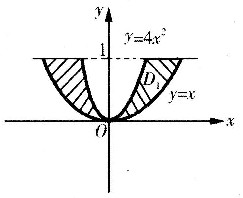
由于区域D关于y轴对称
x是关于x的奇函数,y是关于x的偶函数
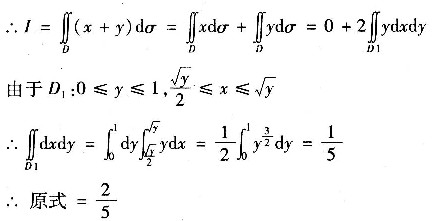
四、综合题1. (1)已知函数x+y+z=sin(x+y+z),求z对x,y的一阶与二阶偏导数;
(2)已知函数
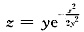
,求dz.
(1)令F(x,y,z)=x+y+z-sin(x+y+z),则
F
x=F
y=F
z=1-cos(x+y+z).
故
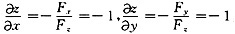
,
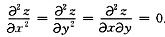
(2)
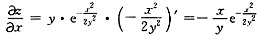

所以
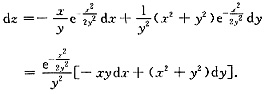
[考点点击] 本题考查隐函数求导和全微分.
2. 求函数f(x,y)=x
3-4x
2+2xy-y
2+1的极值.
∵fx(x,y)=3x2-8x+2y=0
fy(x,y)=2x-2y=0
∴得驻点为(0,0),(2,2)
而fxx(x,y)=6x-8 fxy(x,y)=2 fyz(x,y)=-2
对于(0,0),有B2-AC=-12<0,A=-8<0
所以(0,0)是f(x,y)的极大值点,极大值为f(0,0)=1
对于(2,2),有B2-AC=12>0,所以(2,2)不是f(x,y)的极值点.
综上所述,f(x,y)在(0,0)处取得极大值为1.
3. 求曲z=xy包含在圆柱x
2+y
2=1内部分的曲面面积S.
设所求曲面∑面积为S,该曲面在Oxy坐标面上的投影D:x
2+y
2≤1.
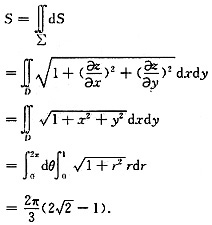
[考点点击] 主要考查的知识点为重积分的应用.