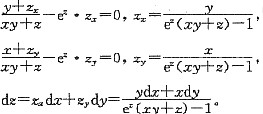一、选择题2. 设函数z=e
x+y
2,则
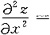
A B C D
D
[解析] 本题考查了二元函数的二阶偏导数的知识点.
[应试指导] 因为z=e
x+y
2,所以
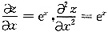
.
4. 设函数y=f(x)的导函数y'=f'(x)的图像如图4-1所示,则下列结论肯定正确的是
.
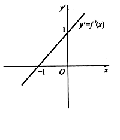
- A.x=-1是驻点,但不是极值点
- B.X=-1不是驻点
- C.x=-1为极小值点
- D.X=-1为极大值点
A B C D
C
[解析] 本题主要考查极值的充分条件及驻点的概念.由f'(x)的图像可知,在x=-1时,f'(-1) -0,所以x=-1为驻点,排除B.而当x<-1时,f'(x)<0;x>-1时f'(x)>0.根据导数符号由负变正,可知x=-1为函数的极小值点.所以选C.
本题也可以由y'(x)的图像而得了y'=x+1,则原函数为
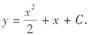
从而很容易得知选项C是正确的.
对于这种由函数导数的图像来分析和研究函数特性的方法建议考生多做练习,熟练掌握.如果本题换一种提法则可以得到另外两个选择题.
(1)设函数y=f(x)的导函数y'=f'(x)的图像如图4-1所示,则函数y=f(x)的单调递增区间为
A.(-∞,1) B.(-∞,+∞) C.(-1,+∞) D.(0,+∞) (C)
(2)设函数y=f(x)的导函数y'=f'(x)的图像如图4-1所示,则下列结论肯定正确的是
A.在(-∞,-1)内,曲线y=f(x)是凸的
B.在(-∞,+∞)内,曲线y=f(x)是凹的
C.在(-∞,+∞)内,曲线y=f(x)是凸的
D.在(-∞,+∞)内,曲线y=f(x)是直线 (B) 由于y'=x+1,则有y"=1>0,从而可以判定曲线y=f(x)在(-∞,+∞)内是凹的,所以选B
二、填空题1.
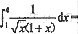
______.
[解析]
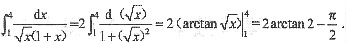
2. 设
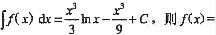
______.
x2lnx
[解析] 因为f(x)=[∫f(x)ax]’,
而
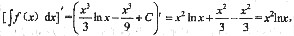
所以
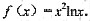
3.
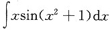
=______.
[解析] 用凑微分法积分.
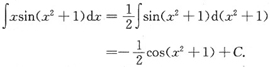
4.
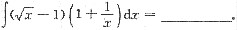
[解析]
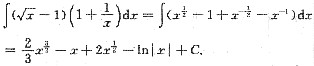
5. 设y=3
sinx,则y’=______.
3sinxln3·cosx
[解析] y’=ln3-3sinx(sinx)’=3sinxln3·cosx·
6. 已知y=(1+x)
5,则dy|
x=0=______。
7. 设函数y=sin(lnx),则y'=______
8.

9. 已知(cotx)’=f(x),则∫f'(x)dx=______.
[解析] ∫f’(x)dx=∫xdf(x)=xf(x)-∫f(x)dx
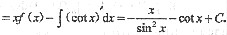
10. 由方程xy-e
x+e
y=0确定的隐函数的导数y'=______.
[解析] 方法一 两边对x求导y+xy'-e
x+e
y·y'=0,
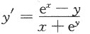
方法二 令F(x,y)=xy-e
x+e
y=0.
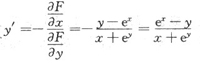
三、解答题1.

2.
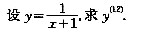
[解析] 求高阶导数,不能采取简单的逐阶求导方法,其关键是找出规律.
3. 已知函数f(x)=ax
3-bx
2+cx在区间(-∞,+∞)内是奇函数,且当 x=1时f(x)有极小值
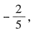
,求a,b,c.
本题考查的知识点是奇函数的概念、极值的概念及极值的必要条件.
[解析] 如果函数是一个m次多项式,且是奇(或偶)函数,则一定有偶次幂(或奇次幂)项的系数为0.再利用极值的必要条件及极值即可求出a,b,c
解 因为f(-x)=-f(x),即
-ax
3-bx
2-cx=-ax
3+bx
2-cx
得 2bx
2=0 对a∈R都成立,必有b=0.
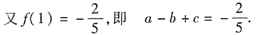
由极值的必要条件:f'(1)=0,得3a-2b+c=0,解得
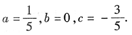
4. 有10件产品,其中8件是正品,2件是次品,甲、乙两人先后各抽取一件产品,求甲先抽到正品的条件下,乙抽到正品的概率.
设事件A表示甲抽到正品,事件B表示乙抽到正品.
方法一:在缩小的样本空间求条件概率
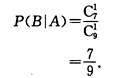
方法二:

由条件概率公式:
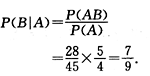
5. 设二元函数z=arcsin(
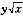
),求
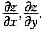
[解析] 求偏导时只需注意:对x求偏导时y当作常数,对y求偏导时,x看作常数再用一元函数的求导公式求导即可。
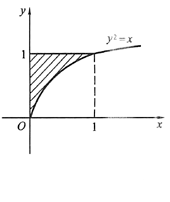
6. 求曲线y
2(上标)=x及直线x=0,y=1围成的平面图形的面积S及此平面图形绕x轴旋转一周所得旋转体的体积Vx.
本题考查的知识点是利用定积分计算平面图形的面积和旋转体的体积.
提示旋转体的体积应为

解 画出平面区域如图4-2阴影区式域所示.则
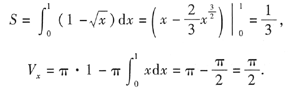
7.
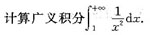
8. 函数z=z(x,y)由ln(xy+z)-e
z-2所确定,求dz。
方程两边分别关于x,y求偏导数