三、解答题1.

(1)求X的分布列;
(2)求数学期望EX
本题考查的知识点是由随机变量X的概率分布函数F(x)求其分布列的方法以及由分布列求其数学期望.
[解析] 由分布函数F(x)求分布列的关键是在各个间断点处的跃度即为各向断点处随机变量X取值时的概率.由F(x)可以知道X可能取的值为-1,0,1,2,而函数F(x)在间断点x=-1的跃度为0.2即随机变量X=-1时的概率为P=0.2;在点x=0处的跃度为0.5-0.2=0.3,即X=0时的概率为P=0.3;同理,在点x=1和点x=2处的跃度分别为0.7-0.5=0.2,1-0.7 =0.3.这样X的分布列和数学期望EX就可以求出了.
解 (1)
X |
-1 |
0 |
1 |
2 |
P |
0.2 |
0.3 |
0.2 |
0.3 |
(2)EX=(-1)×0.2+0×0.3+1×0.2+2×0.3=0.6.
2.
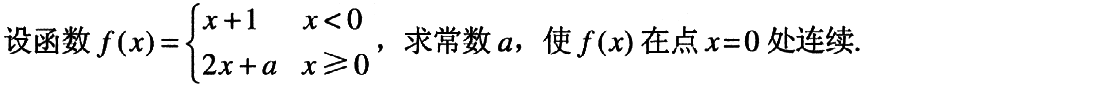
3. 计算
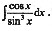
4. 曲线y=f(x)过原点,且在点x处的斜率为4x,求

曲线过原点,则f(0)=0,且f’(x)=4x,因此
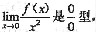
所以有
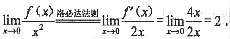
5.

本题的关键是求出切线与坐标轴的交点.
解 如图5-2所示,因为
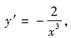
,所以切线方程为
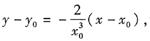
,设切线与两坐标轴的交点分别为(a,0)(0,6),由切线方程可得
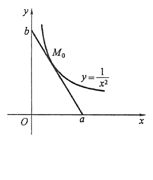

所截线段长度的平方为
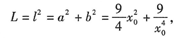
上式两边对x0求导得
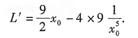
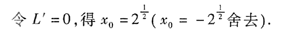
由于只有唯一的驻点,所以

必为所求,所以点Mo的坐标为
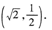
6.
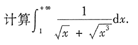
先用换元法去根号,再积分.
解
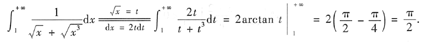
8. 当x→0时,无穷小量
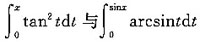
中哪一个是高阶的无穷小?